Описание учебного гониометра

Определение длины световой волны при помощи

Дифракционной решетки

Цель: Изучение явления дифракции света.

Задача: Определение длины световой волны при помощи дифракционной решетки

Введение

Дифракционная решетка представляет систему прозрачных для видимого света щелей, разделенных непрозрачными промежутками.

Простейшей решеткой является стеклянная пластина, на которой нанесены параллельные между собой прямые алмазные нарезки. Причем ширина щелей (расстояние между двумя соседними нарезками) порядка длины световой волны. На 1 мм ширины пластинки наносится от 50 до 2000 нарезок.

а) Возьмем простейшую решетку из 2-х щелей. Рассмотрим дифракцию Фраунгофера – дифракцию в параллельных лучах. Пусть падают на решетку монохроматические параллельные лучи, т.е. плоские световые волны (радиус кривизны поверхности которых равен бесконечности).

Поверхность плоских волн, т.е. поверхность одинаковых фаз, представляет собой бесконечную плоскость.

Пусть в какой-то момент времени t поверхность плоской волны оказалась в плоскости щелей дифракционной решетки.

По принципу Гюйгенса-Френеля каждая точка поверхности волны является источником сферических когерентных волн, которые, интерферируя между собой, создают неизменные в пространстве за решеткой области усиления световых колебаний (усиления света - max – сплошная линия) и области ослабленных световых колебаний (ослабления света – min – пунктирная линия). См.рис.1.

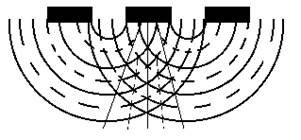Рис.1.

Таким образом, в пространстве за решеткой происходит интерференция света. Чтобы обнаружить эту интерференцию необходимо с помощью собирающей линзы зафиксировать интерференционную картину на экране, расположенного в фокальной плоскости линзы. (На самом деле интерференция происходит в пространстве за решеткой, а экран поможет увидеть результат интерференции – дифракцию света). На экране получаем следующую картину (см.рис.2). Получаем чередование светлых и темных полос. Причем, максимум нулевого порядка наиболее яркий, яркость остальных максимумов убывает по мере возрастания номера порядка. Ширина максимума увеличивается по мере возрастания номера порядка.

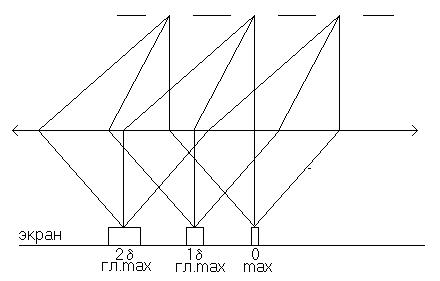Рис.2.

Запишем формулы описывающие дифракцию света в случае двух щелей.

с – постоянная или период решетки (с = а + в);

а – ширина элементарной щели, в - ширина элементарной экрана;

D - разность хода лучей;

j - угол отклонения лучей от перпендикуляра к решетке.

Условие максимума: с sinj = 0, l, 2l, 3l, 4l, 5l, 6l, ... , kl;

Условие минимума: с sinj =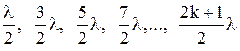

Общее условие максимума и минимума:

с sinj =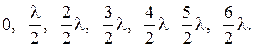

В случае двух щелей между двумя соседними главными максимумами находится по одному минимуму.

б) Возьмем решетку из 4-х щелей. Причем постоянную с берем такой же, что и для двух щелей.

1) Условие максимума и минимума для щелей 1 и 2, 3 и 4 сведется к условию максимума и минимума для двух щелей, полученному выше.

Перепишем: с sinj =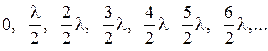

или с sinj =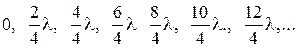

2) Условие максимума для щелей 1 и 3, 2 и 4:

2с sinj = 0, l, 2l, 3l, 4l, 5l, 6l, ...

или с sinj =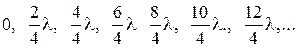

3) Условие минимума для щелей 1 и 3, 2 и 4:

2с sinj =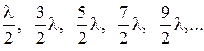

или с sinj =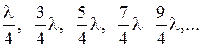

4) Общее условие максимума и минимума для четырех щелей:

с sinj =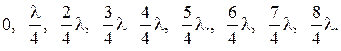

Из последовательности видно, что между двумя соседними главными максимумами находятся три добавочных минимума. Если число щелей N (в нашем случае N = 4), то между двумя соседними главными максимумами появляются (N-1) добавочных минимумов (в нашем случае 4 -1 = 3).

Для наглядности начертим график распределения интенсивностей главных максимумов для 2-х и 4-х щелей.

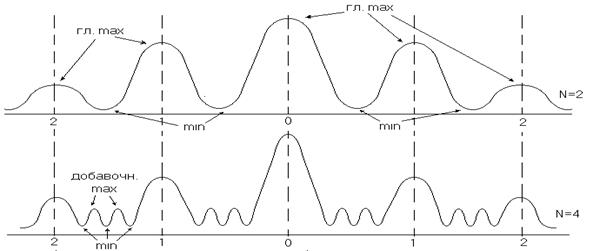рис.3

По оси ординат откладываем интенсивность главных максимумов, по оси абсцисс расстояние между главными максимумами.

В случае N щелей с той же постоянной решетки С общее условие минимума и максимума запишется:

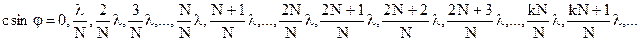При рассмотрении дифракции света на одной щели получается формула:

а sinj = (k + 1)l,

которая автоматически распространяется на решетку. Получаем условие главных максимумов аsinj = (k + 1)l.

Вывод:

1. Между двумя соседними главными максимумами возникает (N-1) минимумов.

2. По мере увеличения числа щелей интенсивность главных максимумов возрастает 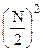раз.

3. По мере увеличения номера дифракционного порядка интенсивность главных максимумов убывает, а ширина увеличивается.

4. с sinj = kl (k = 0,1,2,3,...) является формулой главных максимумов дифракционной решетки.

5. аsinj = (k + 1)l (k = 0,1,2,3,...) является формулой главных минимумов дифракционной решетки.

Дисперсия решетки

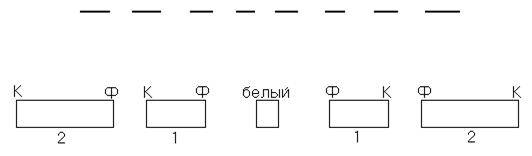
Если решетку осветить белым светом, то все порядки, кроме нулевого порядка, будут спектральными, причем фиолетовый конец всех порядков обращен к нулевому порядку. Нулевой порядок остается белым (см. рис.3). В составе белого света световые волны семи цветов, которые все будут иметь разность хода, равную нулю и удовлетворять условию максимума, т.е. складываясь они будут давать максимум нулевого порядка – белый.

Дисперсией решетки называется производная угла отклонения луча от перпендикуляра к решетке по длине волны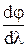

с sinj = kl

с cosdj = kdl

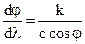
1. Дисперсия решетки (ширина спектра при данном постоянном с) зависит от номера порядка, чем выше порядок, тем шире спектр.

2. Дисперсия решетки (ширина спектра данного порядка) зависит от постоянной решетки с, чем с меньше, т.е. щели уже, тем ширина спектра больше.

Все остальные порядки кроме нулевого являются спектральными, т.к. для света разных длин волн условие max будут под разными углами. Например: k = 1, l₁ < l₂ из формулы с sinj_k = kl, для j (0, 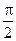)Þ j_l1< j_l2. Следовательно каждый порядок по мере увеличения угла начинается с фиолетового цвета и заканчивается красным, остальные цвета между ними.

Выполнение работы

Направить гониометр (щель) на яркую часть ртутной лампы. Навести нить последовательно на все линии первого порядка, производя при этом отсчеты по лимбу; затем тоже самое

проделать со следующими порядками правых секторов После проверки установки гониометра на нуль, тоже самое проделывают с линиями левых порядков. Все отсчеты занести в таблицу.

Постоянная решетки с = 4^.10 ^–6 м.

таблица

порядок спектра	цвет линий	угол по лимбу	длина волны
вправо	влево	среднее
n =1	Зеленая Желтая 1 красная 2 красная
n=2	Зеленая Желтая 1 красная 2 красная
среднее значение длины волны	Зеленая Желтая 1 красная 2 красная

Ответ: l_з = l_{ср з} ± Dl = … нм

l_ж = l_{ср ж} ± Dl = … нм

l_{к 1} = l_{ср к 1} ± Dl = … нм

l_{к 2} = l_{ср к2} ± Dl = … нм

Литература

1. Королев Ф.Л. Курс физики.

2. Савельев И.В. Курс общей физики. Т.2

3. Матвеев А.М. Оптика.

Описание учебного гониометра

Горизонтальный лимб (круг) гониометра имеет цену деления основной шкалы 1⁰, нониуса 5' и соединен с предметным столиком А, на который ставится дифракционная решетка В.

К столику там, где расположен лимб, прикреплена зрительная труба (ЗТ), в окуляре которой имеется вертикальная нить, устанавливаемая в процессе работы на линии дифракционного спектра.

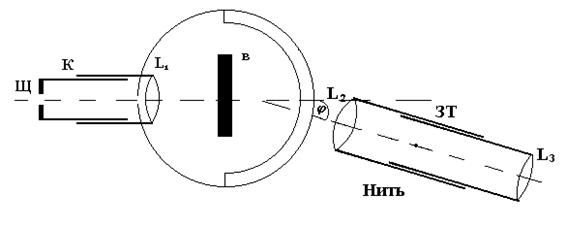
С противоположной стороны к столику прикреплена коллиматорная труба К, имеющая с одной стороны вертикальную щель Щ, с другой - собирательную линзу L₁. Щель коллиматора можно передвигать по отношению к линзе, можно с помощью винта изменять ее ширину.

ЗТ можно поворачивать в горизонтальной плоскости по отношению к столику с лимбом и решеткой.

Юстировка гониометра

Гониометр требует тщательной юстировки, которая заключается в установке зрительной трубы на бесконечность, в установке коллиматора на параллельный пучок лучей, в установке оптической оси гониометра перпендикулярно плоскости дифракционной решетки.