Пространственные методы улучшения изображения. Некоторые градационные преобразования. Гистограмма изображения. Основы пространственной фильтрации

Элементы зрительного восприятия человека

Хотя любая обработка изображений строится на основе математических формулировок, человеческая интуиция и анализ играют центральную роль при выборе того или иного метода обработки среди других, и этот выбор часто совершается на основе субъективного визуального оценивания. Поэтому важно иметь представление о зрительном восприятии человека. Рассмотрим некоторые особенности человеческого зрения.

Значительный интерес представляет способность зрения различать изменения яркости. Классический эксперимент для иллюстрации этого строится следующим образом. Испытуемый смотрит на плоский равномерно освещенный экран (яркость 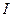можно регулировать), такой, что он занимает все поле зрения. На это поле накладывается дополнительная яркость 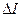в форме кратковременной вспышки в области круглой формы (рис.1.1). 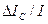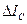Величина , где - значение приращения яркости, различаемая в 50% случаев на фоне яркости 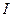, называется отношением Вебера. График зависимости величины 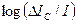от 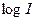изображен на рис.1.2.

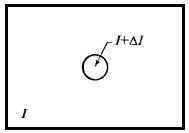
Рис.1.1. Постановка эксперимента для определения характеристик контрастной чувствительности

Если поддерживать фоновую яркость постоянной, а яркость добавочного источника варьировать не вспышками, а ступенчато от неотличимого до заметного всегда, то типичный наблюдатель способен различить всего 10-20 различающихся ступеней яркости.

Примером феномена человеческого зрения являются оптические иллюзии, в которых глаз восполняет несуществующую информацию или ошибочно воспринимает геометрические свойства объектов.

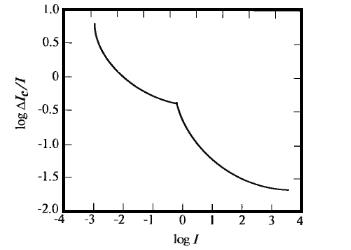
Рис.1.2. Типичная зависимость отношения Вебера как функции яркости

Цифровое изображение

Изображение можно определить как функцию 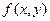, где 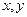- координаты на плоскости, значение 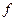которой в любой точке, задаваемой парой координат 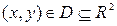, называется интенсивностью или уровнем серого, или градацией серого, или яркостью в этой точке. Если величины 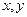, 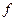принимают конечное число дискретных значений, то говорят о цифровом изображении (ЦИ). Цифровой обработкой изображений называется обработка ЦИ с помощью компьютера. ЦИ состоит из конечного числа элементов, каждый из которых расположен в конкретном месте и принимает определенное значение. Эти элементы называются элементами изображения или пикселями.

Чтобы получить ЦИ, необходимо преобразовать непрерывно поступающий сигнал в цифровую форму. Эта операция включает в себя 2 процесса: дискретизацию и квантование.

Главный принцип, лежащий в основе дискретизации и квантования, проиллюстрирован на рис.1.3. Здесь приведено исходное изображение 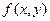, которое мы хотим преобразовать в цифровую форму. Изображение непрерывно по координатам 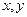, а также по амплитуде 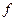. Чтобы преобразовать эту функцию в цифровую форму, необходимо представить ее отсчетами по обеим координатам и по амплитуде. Представление координат в виде конечного множества отсчетов называется дискретизацией, а представление амплитуды значениями из конечного множества – квантованием.

В результате операций дискретизации и квантования в общем случае возникает матрица действительных чисел.

Предположим, что в результате дискретизации изображения 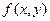получена матрица из М строк и N столбцов. Координаты 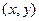становятся теперь дискретными значениями. Для удобства будем использовать для этих координат целочисленные значения (рис.1.4).

Надо помнить, что обозначение, например, (0,1) используется лишь для указания на второй отсчет в первой строке, и не означает, что это фактические значения физических координат точек дискретизации.

Тогда полное ЦИ мы можем компактно записать в виде матрицы:

.

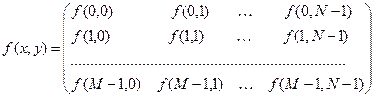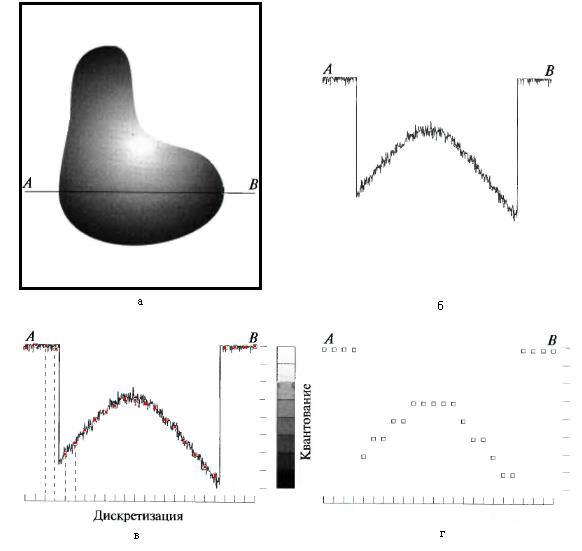
Рис.1.3. Формирование ЦИ. Непрерывное изображение (а). Профиль вдоль линии сканирования между точками А и В на непрерывном изображении, который используется для иллюстрации понятий дискретизация и квантование (б). Дискретизация и квантование (в). Цифровое представление строки изображения (г).

Каждый элемент этой матрицы – элемент изображения или пиксель. Далее будем использовать более традиционную матричную запись:

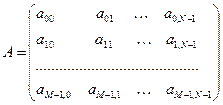
Для выполнения процесса оцифровки изображения необходимо принять решение относительно значений М и N, а также числа уровней (градаций) яркости L, разрешенных для каждого пикселя. Для М и N не существует специальных требований помимо того, что они должны быть натуральными. А значение L, по соображениям удобства построения оборудования для обработки, хранения и дискретизации, обычно выбирают 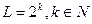, где 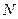- множество натуральных чисел. Мы предполагаем, что дискретные уровни яркости расположены с постоянным шагом (т.е. используется равномерное квантование) и принимают целые значения в интервале 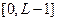. Интервал значений яркости называют динамическим диапазоном изображения.

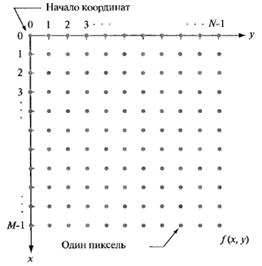
Рис.1.4. Система координат для представления цифровых изображений

Дискретизация является главным фактором, определяющим пространственное разрешение изображения. По существу, пространственное разрешение – это размер мельчайших различимых деталей на изображении.

Яркостным или полутоновым разрешением называется мельчайшее различимое изменение яркости. При выборе числа градаций яркости приходится в значительной степени учитывать особенности аппаратуры. Наиболее частым является выбор 8-битного представления (256 градаций серого) .

В качестве очень грубого эмпирического правила можно считать, что минимальные пространственное и яркостное разрешение, при котором ЦИ будет относительно свободным от дефектов типа ложных контуров и ступенчатости, составляет около 256*256 пикселей с 64 градациями яркости.

Пространственные методы улучшения изображения. Некоторые градационные преобразования. Гистограмма изображения. Основы пространственной фильтрации

Главная цель улучшения ЦИ заключается в такой его обработке, чтобы результат оказался более подходящим с точки зрения конкретного применения.

Множество подходов к улучшению ЦИ распадается на две большие категории: методы обработки в пространственной области и методы обработки в частотной области. Термин пространственная область относится к плоскости изображения как таковой (манипуляции непосредственно с пикселями изображения). Методы в частотной области основываются на модификации сигнала, формируемого путем применения к ЦИ преобразования Фурье.

Общей теории улучшения изображений не существует.

Пространственная область – это множество пикселей, составляющих ЦИ.

Процедуры пространственной обработки описываются общим уравнением:

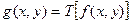
где 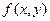- входное ЦИ, 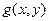- обработанное, а 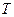– оператор над 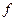, определенный в некоторой окрестности точки 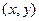, для которой эта точка является центром (рис.1.5). Центр окрестности передвигается от пикселя к пикселю, начиная с верхнего левого угла. Оператор 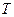выполняется для каждой точки 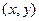, давая в результате выходное значение 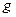для данной точки. Процесс использует только пиксели внутри области ЦИ, ограниченной окрестностью (рис.1.5).

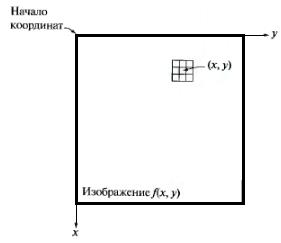
Рис.1.5. Окрестность 3*3 вокруг точк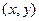и ЦИ

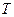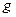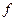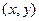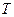Простейшая форма оператора достигается, когда окрестность имеет размеры 1*1 (один пиксель). В этом случае зависит только от значения в точке , и называется функцией градационного преобразования (функцией преобразования интенсивностей или функцией отображения) вида

,

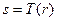где 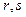- переменные, обозначающие соответственно значения яркостей изображени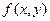й и 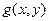в каждой точке 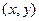. Например, если 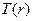имеет вид, показанный на рис.1.6, то эффектом от такого преобразования будет усиление контраста. В предельном случае (рис.1.6(б)) 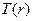дает бинарное ЦИ. Отображение такой формы называется пороговой функцией.

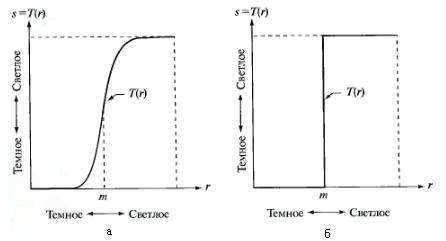
Рис.1.6. Градационное преобразование для улучшения контраста

Увеличение размеров окрестности (рис.1.5) приводит к значительно большей гибкости процесса обработки. Один из основных подходов здесь базируется на использовании так называемых масок (фильтров, ядер, шаблонов или окон). Чаще всего маска представляет собой небольшой (например, 3*3 элемента) двумерный массив (рис.1.5), значения коэффициентов маски внутри которого определяют существо процесса, например, повышение резкости изображения. Методы улучшения, базирующиеся на таком подходе, часто называют обработкой по маске или фильтрацией по маске.