EXAMPLES OF PROBLEM SOLUTION. Example 1. The sphere with radius R=5 cm and the endless uniformly plate are charged from the surfaces with the charge density s1=10 nC/m2 and s1=–15 nC/m2

Example 1. The sphere with radius R=5 cm and the endless uniformly plate are charged from the surfaces with the charge density s₁=10 nC/m² and s₁=–15 nC/m² correspondingly. The sphere’s centre is situated on a distance of ℓ=10 cm from the plate. Find the electric intensity at the point А, which is situated on a distance of а=5 cm from the sphere’s surface and b=10 cm from the plate; force, which will act on the point charge q₀=0,1 nC, if it is put to the point А.

Input data: s1=10 nC/m2=10×10–9 C/m2 s2=–15 nC/m2=–15×10–9 C/m2 R=5 cm =5×10–2 m l=10 см =10×10–2 м а=5 cm=5×10–2 m b=10 cm =10×10–2 m q0=0,1 nC=0,1×10–9 C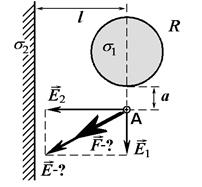
Find: Е, F – ?

Solution:

According to the principle of superposition of electric fields: the sphere creates the electric field irrespective of the plate position in the space, and vice versa: the plate electric field is independent of the sphere position. That’s why the resultant intensity equals the vector sum of the individual intensities:

.

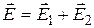a) We must show the directionof the resultant vector of electric intensity defined by parallelogram ruleto the diagrammatic drawing(see picture).

b) We define the magnitude of the resultant vector by cosine theorem:

.

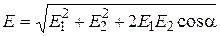Let’s find the individual intensities creating with the sphere and plate.

The sphere’s field intensity is in the point at a distance of r from its centre

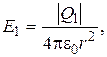(1)

where e₀=8.85×10^-12F/m – the vacuum permittivity; Q₁ – the charge of sphere.

Let’s find the charge of the sphere through the surface charge density s₁ and the area of sphere surface S=4pR²:

.

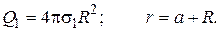In this equation from the point А to the centre of the sphere distance r is defined as a sum of the distance a to the surface of sphere and radius of sphere R.

Inserted these expressions in the formula (1), we’ll get

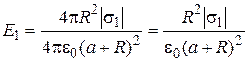. (2)

The plate electric intensity of the uniformly charged with the surface density s₂

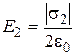. (3)

The vector 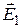is directed along to field line from the sphere, as the sphere is positively charged. The vector 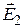is directed to the plate, as the plate is negatively charged.

As the vector 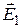and vector 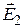are mutually perpendicular and cos90^О=0, then cosine theorem is transformed to a Pythagorean theorem:

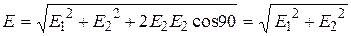. (4)

Putting (2) and (3) in (4) and removing a common factor 1/e₀ beyond the radicand, we’ll get

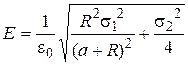. (5)

2. The magnitude of force, which is exerted with the point charge 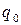,which is situated in the electrostatic field, is defined with the formula

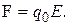(6)

We check if the formula (5) gives unit of intensity V/m, and the formula (6) the unit of force N.

;

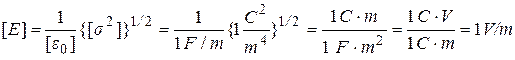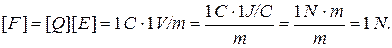
Let's make substitution in the formulas (5) and (6) the value of quantities in the units of SI-system and make the evaluations

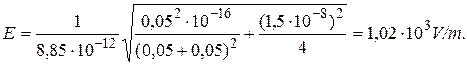
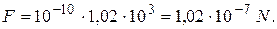
A direction of force coincides with a direction of vector 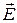. (as 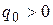), that is shown in the picture.

Results: ,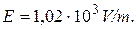

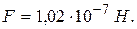
Example 2. The air cylindrical capacitor consists of two coaxial cylinders with radiuses R₁ =1 cm and R₂ =3 cm. The length of the cylinders is L=50 cm. The capacitor was charged with the voltage U=100 V.

Find: 1) the electro capacity of capacitor; 2) field intensity in the capacitor at a distance of r=2 cm from the axle of the cylinders.

Input data: R1= 1cm =0,01m; R2=3cm = 0,03m; L=50 cm =0.5m; U=100 V; r =2cm =0,02m;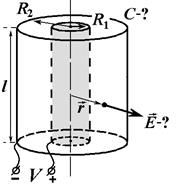
Find: С; E – ?

Solution:

The electro capacity of the air (e=1) cylindrical capacitor can be found with the formula

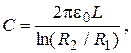(1)

where e₀=8.85×10^-12F/m – the vacuum permittivity; L – the length of cylinders; R₁ and R₂ – radiuses of cylinders.

Let’s find the vector of electric intensity at the distance of r from the axle of cylinders, at the point А, we’ll use the principle of superposition of electric fields

,

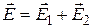where 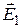– electric intensity at the point А, created with the inner cylinder; 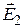– electric intensity of the exterior cylinder at the same point. As it is necessary to find the intensity at the distance of r <R₂ , then Е₂=0 and Е=Е₁. Supposing, that the cylinder is rather long (r<<L), the necessary intensity is found with the formula of calculation of the field intensity of the endless cylinder

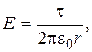(2)

where 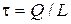– the linear density of the cylinder charge. When one applies the voltage U to the terminals of capacitor, then the charge Q will be induced on the cylinders:

Q=CU. (3)

Putting the expressions for t and Q to the equation (2), we obtain

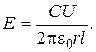(4)

We check if the formula (1) gives unit of capacitance F, and the formula (4) the unit of electric intensity V/m.

;

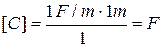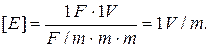
Let's make substitution in the formulas (1) and (4) the value of quantities in the units of SI-system and make the calculations:

;

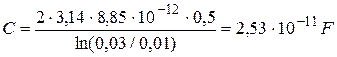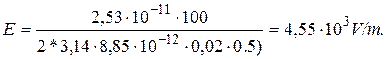
Results: .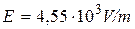

Individual tasks for PROBLEM 1.1.