Общая физика (волны и оптика)
Содержание
| 1.ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ. ПРАВИЛА ОФОРМЛЕНИЯ ИНДИВИДУАЛЬНЫХ ДОМАШНИХ ЗАДАНИЙ………………………………………………… | |
| 2. ОБЩАЯ ФИЗИКА (ВОЛНЫ И ОПТИКА)…............... | |
| 2.1. Основные законы и формулы…………..……. | |
| 2.2. Примеры решения задач………………..….…. | |
| 2.3. Задачи для самостоятельного решения……… | |
| СПИСОК ЛИТЕРАТУРЫ………………………………... | |
| Приложение 1. Таблицы вариантов для ИДЗ……… | |
| ПРИЛОЖЕНИЕ 2 Справочные таблицы ……………..… |
ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПРАВИЛА ОФОРМЛЕНИЯ ИНДИВИДУАЛЬНЫХ
ДОМАШНИХ ЗАДАНИЙ
Учебно-методическое пособие составлено в соответствии с действующей программой дисциплины «Общая физика (Волны и оптика)» для студентов очной формы обучения технических специальностей.
В пособии представлены материалы по разделам:
1. Колебания и волны.
2. Оптика. Квантовые свойства излучения.
В каждом разделе приводится список рассматриваемых тем, варианты задач для самостоятельного решения. Рассмотрены методы и приемы решения типовых задач, способствующие углубленному пониманию физических законов и развитию умения рассуждать (аналитически мыслить). Решения задач выполнены по единой схеме: составлены необходимые уравнения, проведено их решение в общем виде, подставлены числовые данные, выписан ответ.
Согласно рабочему учебному плану в 3 семестре запланировано выполнение индивидуального домашнего задания (ИДЗ).
ИДЗ включает в себя 10 задач. Номера задач, которые должен решить студент, определяются по таблице вариантов (приложение 1). Вариант задания определяется в соответствии с суммой двух последних цифр номера зачетной книжки (студенческого билета). Например, если номер зачетной книжки 120703572, то студент должен выполнять вариант 9 (7+2 = 9), а если номер 120703578, то следует выполнять вариант 15 (7+8 = 15).
При выполнении ИДЗ следует придерживаться следующих правил.
1. Указывать на титульном листе наименование дисциплины, фамилию и инициалы студента, группу, номер зачетной книжки, вариант ИДЗ, шифр и название специальности.
2. ИДЗ следует выполнять аккуратно, оставляя поля для замечаний преподавателя.
3. Задачи своего варианта переписывать полностью, а заданные физические величины выписать отдельно, при этом все числовые величины должны быть переведены в международную систему единиц (СИ).
4. Решение задачи и используемые формулы должны сопровождаться пояснениями. В пояснениях необходимо указывать те основные законы и формулы, на которых базируется решение данной задачи.
5. Для пояснения решения задачи там, где это нужно, аккуратно сделать чертеж.
6. При получении расчетной формулы для решения конкретной задачи приводить ее вывод.
7. Задачу рекомендуется сначала решить в общем виде, т.е. только в буквенных обозначениях, поясняя применяемые при написании формул буквенные обозначения.
8. Вычисления следует проводить с помощью подстановки заданных числовых величин в расчетную формулу. Все необходимые числовые значения величин должны быть выражены в СИ.
9. Проверить единицы полученных величин по расчетной формуле и тем самым подтвердить ее правильность.
10. Константы физических величин и другие справочные данные выбирать из таблиц справочников и приложений используемой литературы.
11. При вычислениях использовать микрокалькулятор для более точного расчета.
12. При предоставлении работы на повторное рецензирование обязательно представлять работу с первой рецензией. Исправленные задачи при повторном предоставлении студентом работы записываются полностью по вышеприведенным правилам.
Рекомендуемая литература
1. Савельев, И.В. Курс общей физики: Учеб. пособие. В 3-х т. Т.1. Механика. Молекулярная физика. СПб.: Лань, 2007. (Учебники для вузов. Специальная литература).
2. Савельев, И.В. Курс общей физики: Учеб. пособие. В 3-х т. Т.2. Электричество и магнетизм. Волны. Оптика. СПб.: Лань, 2007. (Учебники для вузов. Специальная литература).
3.Савельев, И.В. Курс общей физики: Учеб. пособие. В 3-х т. Т.3. Квантовая оптика. Атомная физика. Физика твердого тела. Физика атомного ядра и элементарных частиц. СПб.: Лань, 2007. (Учебники для вузов. Специальная литература).
4. Трофимова Т.И. Курс физики: Учеб. пособие для вузов. – М.: Академия, 2014.
5. Трофимова Т.И., Павлова З.Г. Сборник задач по курсу физики с решениями. М.: Высшая школа, 2002.
6. Чертов А.Г., Воробьев А.А. Задачник по физике: Учебное пособие для втузов. – 8-е изд., перераб. и доп. М.: Физматлит, 2008.
7. Савельев И.В. Сборник вопросов и задач по общей физике: Учебное пособие для студентов втузов. М.: Астрель (изд-во АСТ), 2005.
8. Волькенштейн В.С. Сборник задач по общему курсу физики. М.: Наука, 1985.
9..Трофимова Т.И. Курс физики. Задачи и решения: Учеб. пособие для вузов. М.: Академия, 2012.
10. Детлаф, А.А., Яворский Б.М. Курс физики: Учеб. пособие для втузов. М.: Академия, 2007.
ОБЩАЯ ФИЗИКА (ВОЛНЫ И ОПТИКА)
В данном разделе рассматриваются следующие темы:
- Свободные гармонические колебания, сложение колебаний;
- Затухающие и вынужденные колебания. Переменный ток;
- Упругие волны, электромагнитные волны;
- Геометрическая оптика;
- Интерференция света;
- Дифракция света;
- Поляризация света;
- Законы теплового излучения;
- Фотоэффект. Давление света;
- Эффект Комптона.
По каждой теме приведено по 20 задач для самостоятельного решения.
ОСНОВНЫЕ ЗАКОНЫ И ФОРМУЛЫ
| Кинематическое уравнение гармонических колебаний материальной точки | 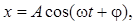 |
| Мгновенная скорость материальной точки, совершающей гармонические колебания | 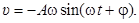 |
| Мгновенное ускорение материальной точки, совершающей гармонические колебания | 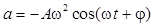 |
| Связь между циклической частотой w, периодом колебаний Т и частотой n | w= 2p /Т = 2pn. |
| Сила, действующая на тело при свободном гармоническом колебании | 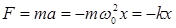 |
| Дифференциальное уравнение свободных колебаний тела массой m, закрепленного на пружине с упругостью k | 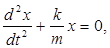 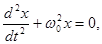 где где 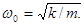 |
| Дифференциальное уравнение свободных электромагнитных колебаний | 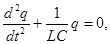 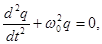  |
| Период колебаний в электромагнитном контуре (формула Томсона) | 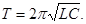 |
| Изменение напряжения на конденсаторе и силы тока в контуре | 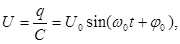 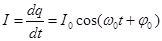 |
| Полная энергия материальной точки, совершающей гармонические колебания | 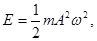 |
| Полная энергия электромагнитного поля колебательного контура | 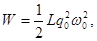 |
| Период колебаний тела, подвешенного на пружине (пружинный маятник) | 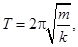 |
| Период колебаний математического маятника | 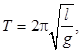 |
| Период колебаний физического маятника | 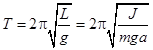 |
| Амплитуда результирующего колебания при сложении гармонических колебаний одного направления и одинаковой частоты | 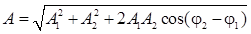 |
| Начальная фаза результирующего колебания | 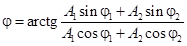 |
| Дифференциальное уравнение затухающих колебаний | 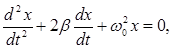 |
| Уравнение смещения в затухающих колебаниях | 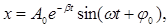 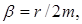 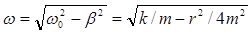 |
| Период затухающих колебаний | 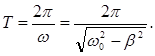 |
| Время релаксации | 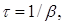 |
| Логарифмический декремент затухания Q | 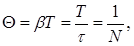 |
| Дифференциальное уравнение затухающих электромагнитных колебаний | 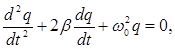 β = R/2L β = R/2L |
| Период и частота затухающих электромагнитных колебаний | 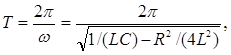 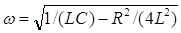 |
| Дифференциальное уравнение вынужденных колебаний | 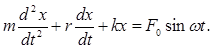 |
| Амплитуда вынужденных колебаний | 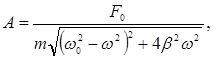 |
| Резонансная циклическая частота и резонансная амплитуда | 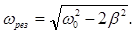 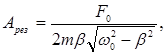 |
| Дифференциальное уравнение вынужденных электрических колебаний | 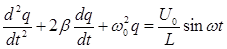 q = q0sin(wt-j), q = q0sin(wt-j), 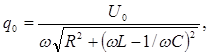 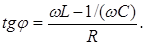 |
| Полное сопротивление цепи | 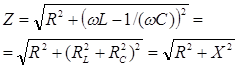 |
| Действующие (или эффективные) значения тока и напряжения | 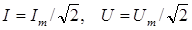 |
| Уравнение плоской бегущей волны | 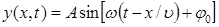 |
| Волновое число | 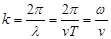 |
| Связь разности фаз Δj колебаний с расстоянием Δх между точками среды, отсчитанным в направлении распространения колебаний, | 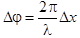 |
| Связь между длиной волны и ее скоростью | 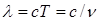 |
| Фазовая скорость | 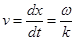 |
| Групповая скорость | 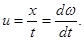 |
| Связь между групповой и фазовой скоростью | 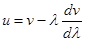 |
| Эффект Доплера | 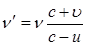 |
| Уравнение электромагнитной волны: | 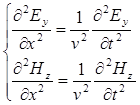 |
| Фазовая скорость v электромагнитных волн | 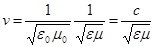 |
| Связь между мгновенными значениями векторов напряженностей электрического Е и магнитного Н полей волны в любой точке | 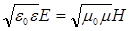 |
| Объемная плотность энергии электромагнитных волн | 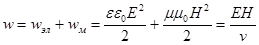 |
| Модуль плотности потока энергии | 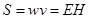 |
| Вектор плотности потока электромагнитной волны (вектор Умова-Пойтинга) | 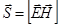 |
| Интенсивность плоской монохроматической бегущей электромагнитной волны | 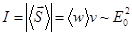 |
| Закон преломления света | 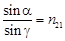 |
| Предельный угол | 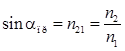 , , 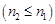 |
| формула тонкой линзы | 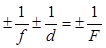 |
| Фокусное расстояние сферического зеркала | F= R/2 |
| Скорость света в среде | 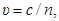 |
| Оптическая длина пути световой волны | 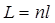 |
| Оптическая разность хода двух лучей равна | 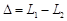 |
| Связь разности фаз с оптической разностью хода | 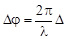 |
| Условие максимума при интерференции | 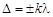 , где k = 0, 1, 2,…. , где k = 0, 1, 2,…. |
| Условие минимума при интерференции света | 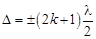 , где k = 0, 1, 2,…. , где k = 0, 1, 2,…. |
| Оптическая разность хода лучей, возникающая при отражении монохроматического света от верхней и нижней поверхностей тонкой пленки, находящейся в воздухе | 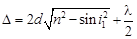 |
| Радиус светлых колец Ньютона в отраженном свете | 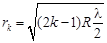 |
| Радиус темных колец Ньютона в отраженном свете | 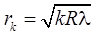 |
| Угол φ отклонения лучей, соответствующий максимуму (светлая полоса) при дифракции на одной щели | 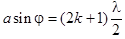 |
| Дифракционный минимум от одной щели | 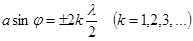 |
| Условие главных максимумов для дифракционной решетки | 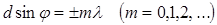 |
| Разрешающая способность дифракционной решетки | 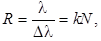 |
| Формула Вульфа–Брэггов | 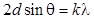 |
| Закон Брюстера | 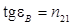 |
| Закон Малюса | 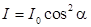 |
| Степень поляризации света | 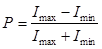 |
| Угол поворота плоскости поляризации φ монохроматического света при прохождении через раствор |  |
| Закон Стефана–Больцмана | 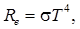 |
| Закон смещения Вина | 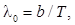 |
| Формула Планка | 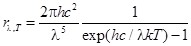 |
| Масса, энергия и импульс фотона | 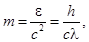 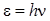 , , 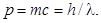 |
| Формула Эйнштейна для фотоэффекта | 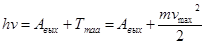 |
| Красная граница фотоэффекта | 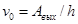 , , 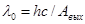 |
| Давление света | 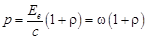 |
| Формула Комптона | 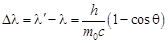 |
| Комптоновская длина волны | 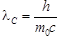 , , 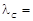 2,436 пм. 2,436 пм. |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1.
Полная энергия тела, совершающего гармонические колебания равна Е = 24 мкДж, максимальная сила, действующая на тело Fmax = 2,0 мН. Написать уравнение движения того тела, если период колебаний Т = 2 с и начальная фаза φ = p/6.
Решение.
1. Полная энергия тела, совершающего гармонические колебания:
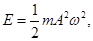 (1)
(1)
где m, А – масса точки и амплитуда ее колебаний; ω – круговая (циклическая) частота.
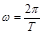 (2)
(2)
2. Согласно второму закону Ньютона сила равна F = ma, откуда максимальная сила:
F max= mamax . (3)
3.Ускорение тела, совершающего гармонические колебания определяется по формуле
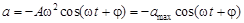 , (4)
, (4)
следовательно,
amax =Аw2 = 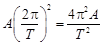 , (5)
, (5)
1. С учетом (5) получим:
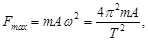 (6)
(6)
5. Выразим амплитуду колебаний А из уравнений (1) и (6):
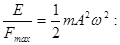
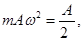
откуда
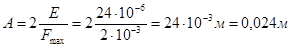
6. Общее уравнение гармонических колебаний:
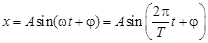 . (7)
. (7)
7. Подставим в (7) числовые значения:
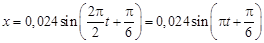 .
.
Ответ: 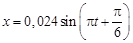 .
.
Задача .2.
Разность потенциалов на обкладках конденсатора в колебательном контуре изменяется со временем по закону U = 100sin1000pt. Электроемкость конденсатора 0, 5 мкФ. Определить период собственных колебаний, индуктивность, энергию контура и максимальную силу тока, текущего по катушке индуктивности.
Решение.
1.Напряжение на обкладках конденсатора меняется по гармоническому закону
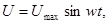 (1)
(1)
где Umax – максимальное значение напряжения на обкладках конденсатора, w – собственная циклическая частота колебаний, которая связана с периодом соотношением
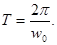 (2)
(2)
По условию задачи, U = 100sin1000pt, таким образом, имеем:
Umax = 100В, w = 1000p с-1,
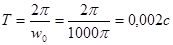 .
.
2. Период собственных колебаний в контуре определяется по формуле
Томсона 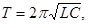 откуда
откуда
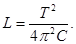 (3)
(3)
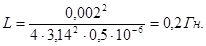
3. Энергия контура равна максимальной энергии поля конденсатора
Wэ max или максимальной энергии катушки индуктивности Wм max:
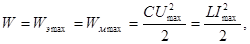 (4)
(4)
откуда 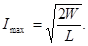 (5)
(5)
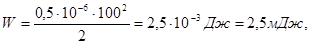
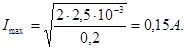
Ответ: Т = 2 мс, L = 0,2 Гн, W = 2,5 мДж, Imax = 0,15А.
Задача 3
Энергия затухающих колебаний маятника, происходящих в некоторой среде, за время t= 2 мин, уменьшилась в N = 100 раз. Определить коэффициент сопротивления, если масса маятника m =0,1 кг.
Решение.
1.Коэффициент сопротивления r связан с коэффициентов затухания b и массой тела m соотношением
r = 2mb. (1)
2.Полная энергия тела, совершающего гармонические колебания, определяется формулой
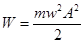 (2)
(2)
3. Обозначим начальное и конечное значение энергии колебаний через W0 и W соответственно, и найдем отношение данных величин c учетом исходных данных:
W0/W = (A0/A)2 = N, (3)
откуда
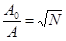 . (4)
. (4)
Для затухающих колебаний имеет место соотношение
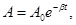 (5)
(5)
откуда
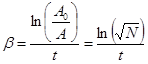 . (5)
. (5)
C учетом (5) выражение (1) примет вид
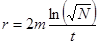 . (6)
. (6)
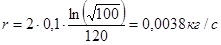
Ответ:r =0, 0038 кг/с.
Задача 4.
Звуковые колебания, имеющие частоту ν = 500 Гц и амплитуду A = 0,3 мм, распространяются в воздухе. Длина волны λ = 60 см. Найти скорость υ распространения колебаний и максимальную скорость частиц воздуха.
Решение.
1). Скорость распространения колебаний (фазовая скорость) равна
υ =λn (1)
где λ - длина волны; n - частота колебаний.
υ = 0,6·500 = 300 м/с.
2). Уравнение плоской бегущей волны, распространяющейся вдоль координатной оси x, имеет вид
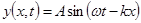 , (2)
, (2)
где у – смещение любой из точек среды с координатой х в момент t; υ – скорость распространения колебаний в среде; A – амплитуда колеблющихся точек; k = 2 π /λ – волновое число.
3.Найдем скорость точек среды, в которой распространяется волна, путем дифференцирования волнового уравнения по вчремени:
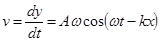 , (3)
, (3)
4. Скорость частиц в воздухе будет максимальной, если 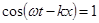 , тогда
, тогда 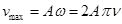 . (4)
. (4)
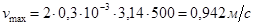
Ответ: υ = 300 м/с; 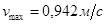 .
.
Задача 5
Луч падает на плоскопараллельную пластину под углом a = 30°. Выходящий из пластинки луч параллелен падающему лучу (рис.1). Показатель преломления стекла n = 1,5. Какова толщина пластинки, если расстояние между лучами СD =3,88 см?
Решение.
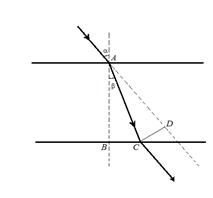 рис.1.1 рис.1.1 | 1.Из рисунка видно, что углы a и Ð BAD – вертикальные, поэтому Ð BAD = a, Ð СAD = a - β. (1) 2.Треугольники СAD и АВС – прямоугольные, и для них справедливы соотношения: 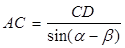 , (2) , (2) 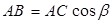 . (3) 3. Подставим (2)в (3) и получим . (3) 3. Подставим (2)в (3) и получим |
выражение для нахождения толщины пластинки АВ:
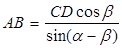 . (4)
. (4)
4.Угол преломления β определим из закона преломления 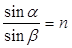 ,
,
откуда
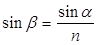 ,
, 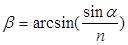 . (5)
. (5)
5. Подставим числовые значения:
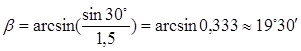
a - β = 30°- 19° 30¢ = 10° 30¢.
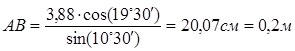
Ответ: АВ= 0,2 м.
Задача 1.6.
Для уменьшения потерь света при отражении от стекла на поверхность объектива (n2= 1,7) нанесена тонкая прозрачная пленка (n = 1,3). При какой наименьшей толщине ее произойдет максимальное ослабление отраженного света, длина волны которого приходится на среднюю часть видимого спектра (l0 = 0,56 мкм)? Считать, что лучи падают нормально к поверхности объектива.
Решение.
1.Свет, падая на объектив, отражается как от передней, так и от задней поверхностей тонкой пленки. Ход лучей для случая их наклонного падения изображен на рис. 1.2.
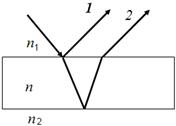 Рис. 1.2 Рис. 1.2 |
Отраженные лучи 1, 2 интерферируют. Условие минимума интенсивности света при интерференции выражается формулой
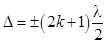 , (1)
, (1)
где k = 0,1,2,…
2.Оптическая разность хода лучей, отраженных от двух поверхностей тонкой пленки, окруженной одинаковыми средами, определяется формулой
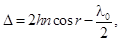 ( 2)
( 2)
где h – толщина пластинки, n – показатель преломления (абсолютный) вещества пластинки, r – угол преломления, l0 – длина световой волны в вакууме.
В данном случае пленка окружена различными средами – воздухом (n = 1,00) и стеклом (n2= 1,7). Из неравенства n1 < n < n2 следует, что оба луча 1, 2, отражаясь от границы с оптически более плотной средой, «теряют» полуволну. Так как это не влияет на их разность хода, то в (2) следует отбросить член l0 /2. Кроме того, полагая r = 0, получим
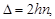 (3)
(3)
3. Из равенств (1), (3) находим толщину пленки:
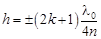 , (4)
, (4)
4. Учитывая, что h – положительная величина и что значению hmin соответствует k = 0, получим:
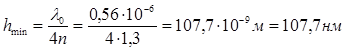
Ответ:hmin = 107,7 нм.
Задача 7
На установке для наблюдения колец Ньютона был измерен в отраженном свете радиус темного кольца (m = 3). Когда пространство между плоскопараллельной пластинкой и линзой заполнили жидкостью, то тот же радиус стал иметь кольцо с номером, большим на единицу. Определить показатель преломления n жидкости.
Решение.
1.Радиус темного кольца Ньютона в отраженном свете
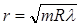 . (1)
. (1)
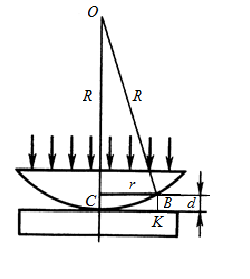 Рис.1.3 Рис.1.3 | 2.Получим выражение для радиуса кольца при заполнении пространства между линзой и пластинкой жидкостью. Рассмотрим для этого прямоугольный треугольника СОВ (рис.1.3): 𝑟2 = 𝑅2−(𝑅−d)2 = (2𝑅 − 𝑑 )𝑑 = 2𝑅𝑑, (2) где d – очень малая величина, 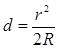 (3) 3. Луч, доходящий до точки В, частично отражается, а частично проходит в воздушный клин. Отражаясь от (3) 3. Луч, доходящий до точки В, частично отражается, а частично проходит в воздушный клин. Отражаясь от |
пластинки в точке К, он возвращается обратно и интерферирует с лучом, отраженным в точке В. Так как в точке К происходит отражение от оптически более плотной среды и теряется полволны, то оптическая разность хода обоих интерферирующих лучей:
Δ = 2𝑑+l/2 (4).
4.Заменим в (4) 𝑑 на ее выражение (3):
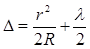 . (5)
. (5)
5.Радиусы темных колец найдем из условия минимума интенсивности для разности хода:
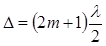 (6)
(6)
или
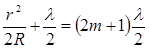 (7)
(7)
6.Отсюда радиус m-го темного кольца
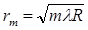 (8)
(8)
7.Учитывая коэффициент преломления, получаем следующую формулу для нахождения радиусов темных колец в отраженном свете:
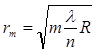 (9)
(9)
8. По условию задачи:
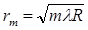 ,
, 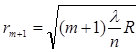 (10)
(10)
так как 𝑟𝑚 = 𝑟𝑚+1, то
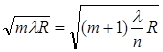 (11)
(11)
9.Выразив из (11) n, получим
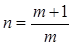 (12)
(12)
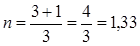
Ответ: n = 1,33.
Задача 8.
На дифракционную решетку падает нормально монохроматический свет с длиной волны 0,6 мкм. На экране, расположенном на расстоянии 0,55 м, наблюдается дифракционная картина, где расстояние между дифракционными максимумами первого порядка равно 12 см. Определить постоянную дифракционной решетки и общее число главных максимумов, получаемых с помощью данной решетки.
Решение.
1. Запишем условие главных максимумов дифракционной решетки:
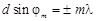 , (1)
, (1)
где d – постоянная решетки, m – порядок главного дифракционного максимума,j – угол между нормалью к решетке и направлением на максимум с порядком m, l – длина волны падающего на решетку света.
2. По условию задачи m = ± 1. Учитывая, что L >> ℓ, можно записать:
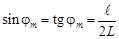 (2)
(2)
3. Подставляя (2) в (1), получим, т.к. d – величина постоянная
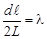 или
или 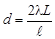 . (3)
. (3)
4.Подставляя в (3) числовые значения величин, находим:
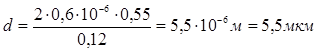
5. Для определения общего числа главных максимумов, даваемых дифракционной решеткой, исходим из условия, что максимальный угол отклонения лучей от нормали к решетке не может превышать 90°, т.е. в формуле (1) sinj < 1, и тогда она принимает вид:
mmax< d/l. (4)
6. Производим вычисления:
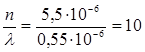 ,
, 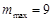 .
.
7. Общее число максимумов N = 2mmax+1, т.е. влево и вправо от центрального (нулевого) максимума будет наблюдаться по mmax максимумов:
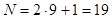
Ответ: d = 5,5 ∙10 – 6 м, N = 19.
Задача 9.
Пластинка кварца толщиной d1 = 1мм, вырезанная перпендикулярно оптической оси кристалла, поворачивает плоскость поляризации монохроматического света определенной длины волны на угол φ1 = 20°. Определить толщину d2 кварцевой пластинки, помещенной между двумя «параллельными» николями, при которой свет будет полностью погашен; длину l трубки с раствором сахара массовой концентрацией С= 0,4 кг/л , помещенной между двумя «параллельными» николями, при которой свет также будет полностью погашен. Удельное вращение [α]раствора сахара равно 0,665град/(м·кг·м-3).
Решение.
1.Угол поворота плоскости поляризации кварцевой пластинкой равен
φ = αd. (1)
где α- постоянная вращения для твердого тела.
- Выразим из (1) искомую толщину d2пластинки и постоянную
вращения для кварца α:
 . (2)
. (2)
где φ2 - угол поворота плоскости поляризации, при котором свет будет полностью погашен (φ2=90°).
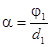 . (3)
. (3)
3.Подставив (3) в (2), получим
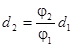 . (4)
. (4)
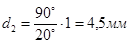
- Длина трубки с сахарным раствором равна
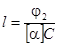 , (5)
, (5)
где φ2 - угол поворота плоскости поляризации раствором сахара; С - массовая концентрация раствора сахара, С= 0,4 кг/л = 400кг/м3 .
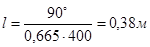
Ответ: d2 = 4,5 мм, l = 0,38 м.
Задача 10.
Вольфрамовая нить накаливается в вакууме током силой I1 = 1,00 А до температуры T1= 1000 К. При какой силе тока нить накалится до температуры Т2= 3000 К? Коэффициенты излучения вольфрама и его удельные сопротивления, соответствующие температурам T1и Т2 равны: aТ1 = 0,115; aТ2 = 0,334; r1 = 25,7×10-8 Ом×м, r2 = 96,2 ×10-8 Ом×м.
Решение.
1. Рассмотрим излучающее тело при установившейся температуре, тогда
Р = Фн , (1)
где Р - мощность, потребляемая вольфрамовой нитью от источника электрической энергии, Фн – поток излучения, испускаемый нитью.
2.Мощность тока
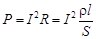 , (2)
, (2)
где l – длина проводника; S – площадь поперечного сечения проводника.
3. Поскольку излучение вольфрама существенно отличается от излучения абсолютно черного тела, нагретого до такой же температуры, то для расчета потока излучения Фн используем соотношение
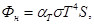 (3)
(3)
где s = 5,67×10-8 Вт/(м2К4) – постоянная Стефана–Больцмана; aТ - коэффициент излучения серого тела.
4. Из (1) – (3) следует, что
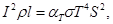 (4)
(4)
Тогда получим:
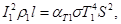 (5)
(5)
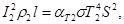 (6)
(6)
- Почленно разделим уравнения (5)и (6):
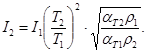 (7)
(7)
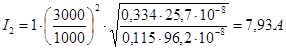
Ответ:I2 = 7,93А
Задача 11.
На зеркальную поверхность нормально падает монохроматический свет с длиной волны 0,55 мкм, производя давление 9 мкПа. Определить концентрацию фотонов вблизи поверхности и число фотонов, падающих на площадь 1 м2 в 1 с.
Решение.
1.Давление света при нормальном падении на поверхность определяется по формуле:
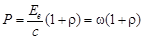 , (1)
, (1)
где Ее – энергетическая освещенность поверхности, т.е. энергия всех фотонов, падающих на единицу поверхности в единицу времени; с – скорость света в вакууме; w – объемная плотность энергии излучения; r – коэффициент отражения поверхности, которой в данном случае равен 1.
2. Объемная плотность энергии равна произведению энергии одного фотона на число фотонов в единице объема:
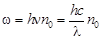 , (2)
, (2)
где h – постоянная Планка. Подставляя (2) в (1), получим:
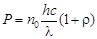 , (3)
, (3)
откуда
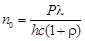 . (4)
. (4)
3.Подставим в (4) числовые значения и проведем вычисления:
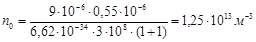
4. Энергетическая освещенность поверхности Ее есть по определению энергия всех фотонов, которые падают на единицу поверхности в единицу времени. Следовательно:
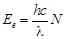 , откуда
, откуда
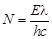 . (5)
. (5)
5. Выразив Ее из (1) и подставив в (5), получим:
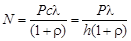 . (6)
. (6)
6.Сравнивая (6) и (4), получаем:
N = п0с.
7. Подставляем числовые значения в полученную формулу:
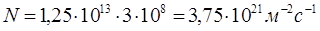
Ответ: 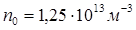 ,
, 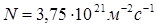 .
.
Задача 12.
Фотон с энергией Е =0,75 МэВ рассеялся на свободном электроне под углом 60°. Принимая, что кинетическая энергия и импульс электрона до соударения с фотоном были пренебрежимо малы, определит энергию Еʹ рассеянного фотона и кинетическую энергию Ек электрона отдачи.
Решение.
1. Энергию рассеянного фотона найдем, воспользовавшись формулой
Комптона:
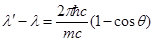 . (1)
. (1)
2. Выразив длины волн λʹ и λ через энергии Еʹ и Е соответствующих фотонов
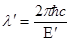 ,
, 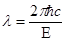
получим:
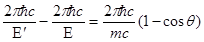 . (2)
. (2)
3. Разделим обе части равенства (2) на 2πħс:
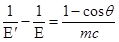 . (3)
. (3)
4. Найдем из (3) энергию Еʹ:
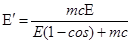 . (4)
. (4)
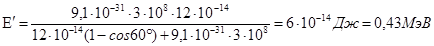
5. Кинетическая энергия электрона отдачи, как это следует из закона сохранения энергии, равна разности между энергией Е падающего фотона и энергией Еʹ рассеянного фотона:
Ек = Е - Еʹ = 0,75 – 0,43 = 0,32МэВ.
Ответ: Еʹ = 0,43МэВ, Ек = 0,32МэВ.
