Послідовність виконання роботи

Рисунок 10.1

Розглянемо випадок ідеальної рідини[1]. Візьмемо довільну трубку струму. Оскільки швидкості частинок рідини напрямлені по дотичних до ліній струму, то при течії рідина не може перетинати бічну поверхню трубки струму. Трубка струму поводиться подібно бічній поверхні жорсткої трубки, уздовж якої тече рідина. Якщо поперечний переріз трубки струму нескінченно малий, то можна вважати, що швидкість рідини одна і та ж у всіх точках одного і того ж поперечного перетину і напрямлена уздовж осі трубки струму. Маса рідини, що протікає за час 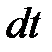через поперечний переріз трубки, визначається виразом

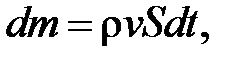(10.1)

де 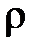– густина рідини, 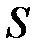– площа (нормального) поперечного перерізу трубки.

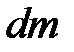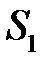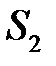У випадку стаціонарної течії маса буде однією і тією ж для всіх перерізів трубки струму. Якщо взяти два перерізи, площі котрих рівні i , то можна записати

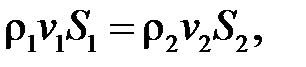(10.2)

Якби ця рівність не виконувалась, маса рідини між перерізами 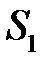i 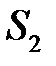з часом змінювалась би. А це суперечить закону збереження маси і припущенню про стаціонарність течії. Якщо рідина нестискувана, то 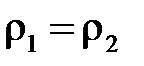, і співвідношення (10.2) приймає вигляд

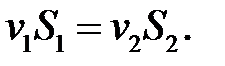(10.3)

Ми отримали рiвняння нерозривностi: добуток швидкостi течiї нестискуваної рiдини на поперечний перерiз трубки є величиною сталою для даної трубки струму. Швидкiсть рiдини в однiй i тiй трубцi тим бiльша, чим бiльш вузький поперечний перерiз трубки.

Рисунок 10.2

Розглянемо стаціонарну течію ідеальної рідини в якому-небудь консервативному силовому полі, наприклад, в полі сили тяжіння. Застосуємо до цієї течії закон збереження енергії. При цьому повністю нехтуватимемо теплообміном, який може відбуватися між частинами рідини з навколишнім середовищем. Виділимо в рідині нескінченно вузьку трубку струму і розглянемо частину рідини, що займає об’єм 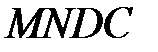(рисунок 10.2). Нехай ця частина перемістилася в нескінченно близьке положення 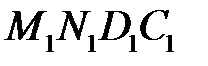. Обчислимо роботу 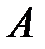, виконувану при цьому силами тиску. Тиск, що діє на бічну поверхню трубки струму, перпендикулярний до переміщення і роботи не виконує. При переміщенні межі 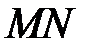в положення 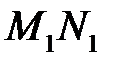виконується робота 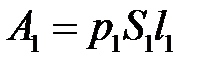, де 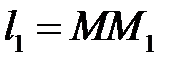— величина переміщення. 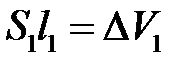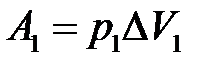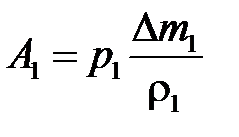, або , де 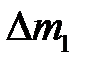—маса рідини в об’ємі 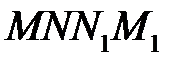. При переміщенні межі 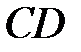в положення 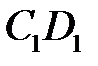рідина виконує роботу проти сил тиску 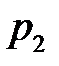(або тиск 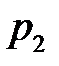виконує над рідиною від’ємну роботу). 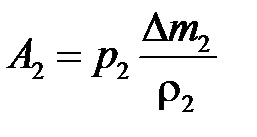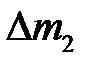Для неї, міркуючи аналогічно, знайдемо де —маса рідини в об’ємі 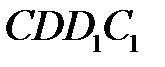. Але якщо рух стаціонарний, то маса рідини в об’ємі 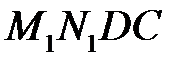не зміниться, а тому із закону збереження маси отримаємо 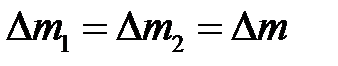. Остаточно знаходимо, що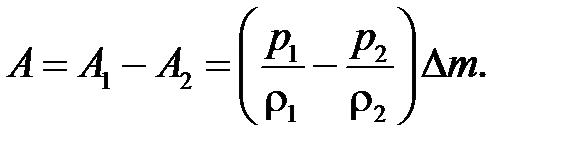

Ця робота рівна приросту 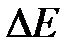повної енергії виділеної частини рідини. Зважаючи на стаціонарність течії, енергія рідини в об’ємі 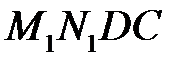не змінюється. Тому величина 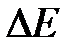рівна різниці енергій маси рідини 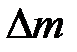в положеннях 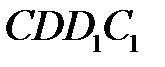i 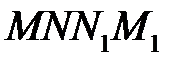. Знаючи повну енергію рідини масою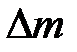

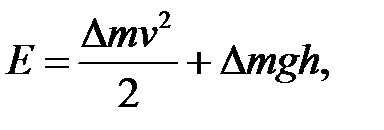
знаходимо 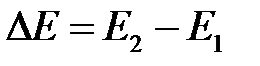. Прирівнюючи цю величину до роботи 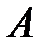і скорочуючи на 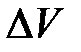, отримаємо

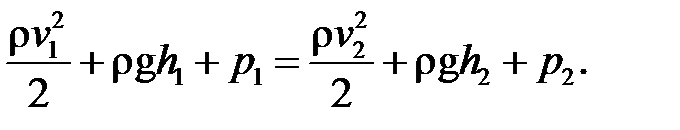(10.4)

Отже,

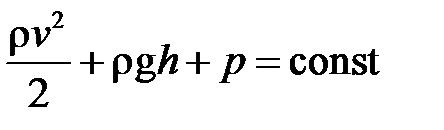(10.5)

– рівняння Бернуллі (1700-1782). Рівняння Бернуллі виражає закон збереження механічної енергії для стаціонарного руху нестислої ідеальної рідини в однорідному полі сил тяжіння.

З рівняння Бернуллі та рівняння нерозривності слідує, що при течії рідини по трубі, яка має різні перерізи, швидкість рідини більша у місцях звуження, а статичний тиск більший в більш широких місцях.

Для горизонтально розташованої трубки (для якої 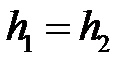) закон Бернуллі має вигляд:

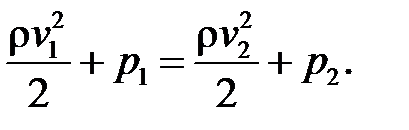(1.6)

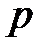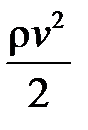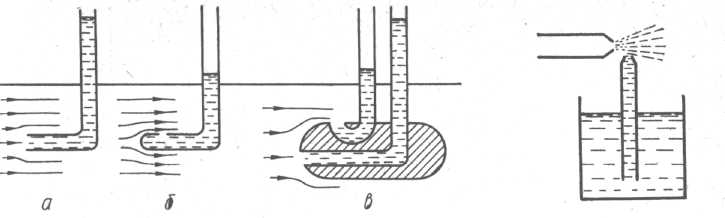
У рівнянні (10.6) тиск називають статичним. Його вимірюють за допомогою манометричних трубок з перерізом, паралельним лінії течії. Для вимірювання складової тиску, зумовленого рухом рідини , застосовують трубки з перерізом, перпендикулярним до лінії течії. Цю складову називають динамічним тиском, а суму 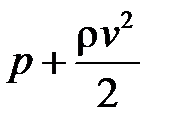називають повним тиском, або повним напором. Для його вимірювання користуються трубкою Піто. Вона являє собою зігнуту мано­метричну трубку, яку розташовують у рухомій рідині так, що її відкритий кінець повернутий назустріч течії рідини (рисунок 10.3, а). Для вимірювання статичного тиску р користуються зондом. Він відрізняється від трубки Піто тим, що його передня частина, яка повернута назустріч потоку рідини, запаяна, а в боковій стінці є невеликий отвір (рисунок 10.3, б). На практиці трубку Піто і зонд сумі­щають в одному приладі, який називають трубкою Прандтля (рисунок 10.3, в). Трубка Піто порушує характер руху рідини, і безпосередньо перед вхідним отвором виникає область, в якій швидкість руху частинок рідини зменшується до нуля ( 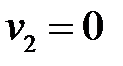). Тоді з рівняння (10.6) дістаємо

.

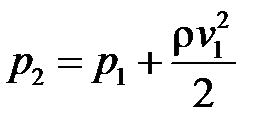За допомогою трубки Прандтля визначають динамічний напір .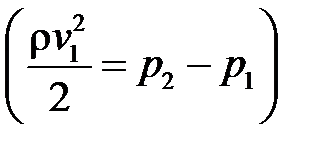

Залежність тиску в рідині від величини її швидкості лежить в основі дії багатьох технічних пристроїв.

Оскільки сума тиску і динамічного напору в потоці рідини стала, то в струмені тиск завжди менший, ніж у нерухомій рідині. При вели­ких швидкостях тиск може стати меншим від атмосферного. Рідина, що протікає через вузьку частину трубки, перебуває в стані все­бічного розтягу. Це явище застосовується в пульверизаторах, кар­бюраторах, водоструминних насосахта в інших приладах. На рисунку 10.4 наведено найпростіший пульверизатор.

Рисунок 10.5 Рисунок 10.6

Рисунок 10.3 Рисунок 10.4

При достатній швидкості течії повітря тиск у звуженій частині трубки буде менший від атмосферного. Внаслідок цього рідина піднімається по вертикальній трубці вгору, оскільки тиск над її верх­нім кінцем менший від атмосферного, який діє на вільну поверхню рідини в посудині. При дальшому збільшенні швидкості повітря в звуженій частині горизонтальної трубки рідина піднімається вище від верхнього перерізу вертикальної трубки, захоплюється струменем повітря і розпилюється. Подібні явища спостерігаються в карбюраторі. Повітря при засмоктуванні в циліндр двигуна внутрішнього згорання рухається по звуженому каналу, в який виходить трубка; другий кінець її знаходиться в рідкому паливі. Звуження каналу зумовлює зниження тиску, внаслідок чого рідке паливо піднімається по трубці і розпилюється повітрям.

Розглянемо течію ідеальної нестискуваної рідини через малий отвір в бічній стінці або дні широкої посудини. Всі лінії струму проходять через трубку, починаючись поблизу вільної поверхні рідини, де швидкість 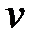зневажливо мала (ми вважаємо, що площа отвору набагато менша за площу вільної поверхні). Застосуємо рівняння Бернуллі до точок 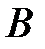і 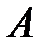і відповідної лінії струму (рисунок 10.5). В точці 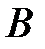швидкість можна вважати рівною нулю, швидкість в отворі 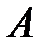позначимо 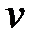. Рівняння Бернуллі дає

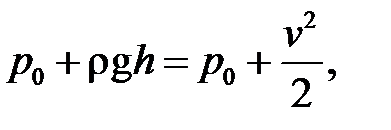
де 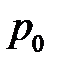— атмосферний тиск, а висота 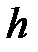відлічується від рівня отвору. Звідси отримуємо

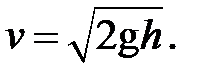(10.7)

Це — формула Торiчеллi (1608–1647). Вона показує, що при витiканнi рiдина отримує таку швидкiсть, яку отримало б тiло, що вiльно падає з висоти h. Тому, якщо зiгнути трубку i направити струю вертикально вгору або пiд малим кутом до вертикалi, то в щонайвищiй своїй точцi вона досягне рiвня рiдини в посудинi. Насправдi висота пiдняття струменя буде дещо менша через тертя i опiр повiтря, якi при отриманнi рiвняння Бернуллi не враховувалися.

В реальних рідинах значення швидкості буде дещо менше, особливо якщо їх в’язкість значна, а отвір має необтічну форму. Коефіцієнт, який характеризує форму отвору, називається коефіцієнтом витікання μ (рисунок 10.6). Тоді формулу Торічеллі для визначення величини швидкості витікання рідини з отвору записують у вигляді: .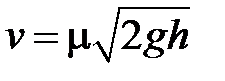

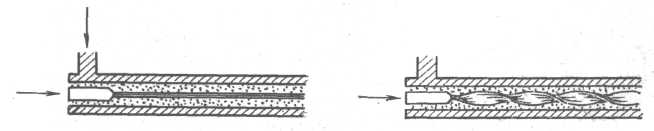
При вивченні руху рідин або газів спостерігаються два види їхнього руху: ламінарний і турбулентний. При ламінарному русі окремі шари рідини неначе ковзають один відносно одного і не пере­мішуються. Швидкості частинок у будь-якому перерізі паралельні між собою. З цього випливає, що ламінарна течіяє стаціонарною. Ламінарну течію можна спостерігати у горизонтальній прозорій трубі, в якій з невеликою швидкістю рухається вода і на осі труби через тонку трубочку вводиться струмина забарвленої рідини. Забарвлена струмина матиме вигляд прямої лінії вздовж осі труби (рисунок 10.7). Із збільшенням швидкості руху характер течії істотно змінює­ться. Ламінарна течія стає нестійкою і переходить у турбулентний потік. При турбулентному потоці частинки рідини здійснюють не­регулярні рухи по складних траєкторіях, а швидкості змінюються хаотично як за напрямом, так і за величиною. Внаслідок цього від­бувається інтенсивне перемішування шарів рідини. Із збільшенням швидкості руху рідини у трубі забарвлена струмина розпливається, утворюючи завихрення (рисунок 10.8). Прикладами турбулентного руху є рух води в бурхливих гірських річках, рух диму, що виходить із труб тощо. Особливо наочним прикладом турбулентного руху повітря є його рух підчас снігової пурги. Турбулентні потоки — це найбільш поширений вид руху рідин і газів у природі. В турбу­лентних потоках часто виникають вихори. Великі вихори нестійкі і розпадаються на дрібніші, більш стійкі.

Рисунок 10.7 Рисунок 10.8

При турбулентній течії середня швидкість по всьому поперечному перерізі потоку майже постійна. У пограничному тонкому шарі ріди­ни, що прилягає до самих стінок труби, швидкість зменшується до нуля. Незважаючи на те що турбулентний потік за своїм змістом нестаціонарний, на практиці його умовно розглядають як стаціонар­ний потік з усередненими характеристиками. Кількісно перехід між режимами (ламінарним і турбулентним) характеризується числом Рейнольдса: 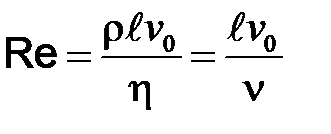,де 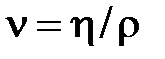– кінематична в‘язкість, 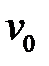– характерна швидкість потоку, 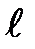– характеристичний розмір.

Величина числа Рейнольдса – порядку відношення кінетичної енергії рідини, що переноситься потоком через заданий переріз за одиницю часу, до величини роботи проти сил в‘язкого тертя, що виконується потоком також за одиницю часу. Отже, число Рейнольдса має порядок величини, яка визначає­ться відношенням кінетичної енергії рідини до втрат енергії, зумовленої роботою сил в'язкості на шляху, що дорівнює характеристичній довжині. Число Рейнольдса визначає відносну роль інерції і в'яз­кості рідини під час течії. При великих числах Рейнольдса основну роль відіграє інерція, а при малих — в'язкість.

Із збільшенням швидкості течії ламінарний рух переходить у турбулентний. Швидкість, при якій відбувається цей перехід, називають критичною. Замість критичної швидкості користуються числом Рейнольдса. Так, якщо за характерний розмір взяти радіус труби, то критичне значення числа Рейнольдса, при якому ламінарний рух переходить у турбулентний, 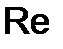=1100. Критичне значення числа Рейнольдса, тобто число 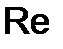, при якому ламінарний рух переходить у турбулентний, визначається тільки експериментально. Число Рейнольдса відіграє важливу роль у всіх кількісних дослідженнях потоку рідини і газів.

Опис установки: рухаючи бігунок в нижній правій частині екрану можна змінювати потужність роботи вентилятора (кількість обертів вентилятора за хвилину). Натисканням кнопки "Старт" розпочинаємо дослід. При включенні установки анемометри на табло показують швидкість повітря у широкій та вузькій частинах труби. Рівень води в манометрових трубках змінюється, що вказує на зміну тиску повітря в різних частинах труби. 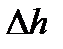Зміну рівня води можна виміряти рухомими стрілками - показниками, при русі яких виміряна величина з'являється на табло. Натисканням кнопки "Стоп" експеримент можна закінчити. Після закінчення можна перейти до наступного завдання, натиснувши кнопку "Завдання". Кнопка ">>" дає змогу перейти до наступного розділу лабораторної роботи, "<<" – повернутися до попереднього, "?" – виводить на екран теоретичні відомості.

Таблиця 10.1– Кількість обертів вентилятора

Варіант
n, об/хв

Послідовність виконання роботи

Досліди з потоком повітря в трубі1. а). Знайдiть зменшення тиску газу в лiвому перерізі труби при роботi вентилятора. Запустiть вентилятор i проведiть необхiднi вимiрювання і розрахунки.б). Знайдiть зменшення тиску газу в правому перерізі труби при роботi вентилятора. Запустiть вентилятор i проведiть необхiднi вимiрювання і розрахунки.2.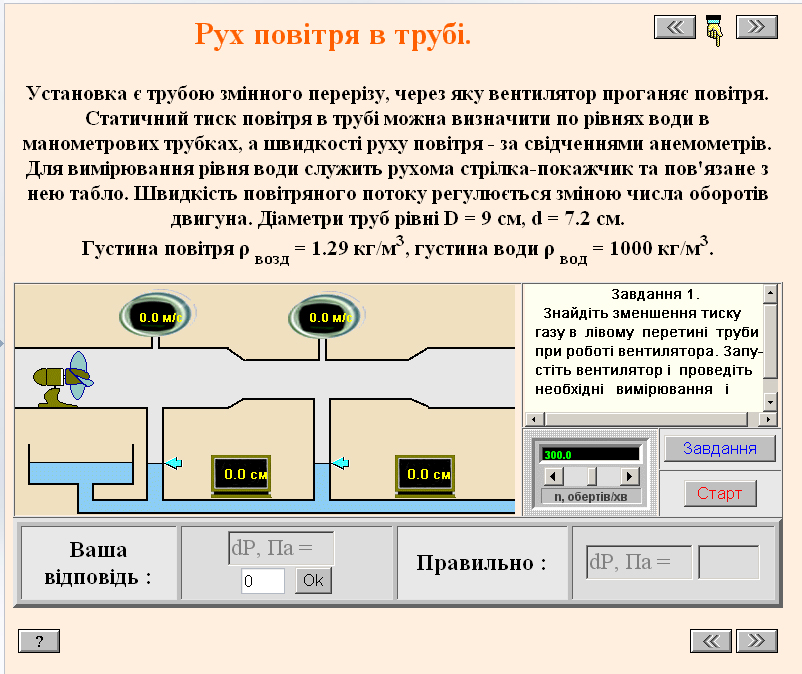
3. Перевiрте справедливiсть рiвняння Бернуллi для рiзних швидкостей повiтряного потоку. За показами анемометрiв визначте рiзницю динамiчного тиску газу в двох перерізах, і зiставте iз змiною статичних тискiв. При збiгу введiть це число у вiкно вiдповiдей. Не забудьте, що всi вимiрювання виконуються з обмеженою точнiстю.4. Один з анемометрiв зiпсувавcя, а манометровi трубки засмiтились. Спробуйте тепер визначити рiзницю динамiчних тискiв в трубi. Отримане число з точнiстю до цiлих введiть у вiкно вiдповiдей.5. Уявiть, що обидва анемометри зiпсованi, але манометровi трубки працюють. Чи зможете Ви визначити, який об'єм повiтря проганяється через трубу за одиницю часу?6. Сформулюйте висновки.Зауваження1. Подумайте i дайте вiдповiдь на питання:Чому вiдбулося зменшення тиску повiтря в трубi пiсля початку роботи вентилятора? Чому стовпчики рiдини пiднялися на рiзну висоту i залишаються нерухомими пiд час роботи вентилятора?2. Для горизонтально розташованої труби закон Бернуллi має вигляд 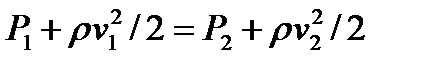,де P - статичний тиск, 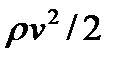- динамічний тиск у вiдповiдному перерізі труби.3. Використовуйте для вирiшення задачi рiвняння нерозривностi струменя.4. Розв’яжіть як систему рiвняння Бернуллi i рiвняння нерозривностi струменя. Дослiдження витікання рiдини з отвору1. Використовуючи рiвняння Бернуллi, визначте швидкiсть витiкання рiдини з отвору.2. За результатами дослідів розрахуйте дальнiсть польоту струменя.3. Побудуйте графiк залежностi дальностi польоту струменя L вiд висоти розташування отвору H. (Для простоти H - цiлi числа.) При якому розташуваннi отвору дальнiсть польоту струменя буде найбільшою?4. Сформулюйте висновки.Зауваження1. Складiть рiвняння Бернуллi для двох перерізів потоку:а) поверхнi рiдини; б) отвору в стiнцi ракети.Врахуйте, що площа отвору у багато разiв менша площi поверхнi рiдини в ракетi.2. Виключiть час з рiвнянь, що описують рух тiла кинутого горизонтально.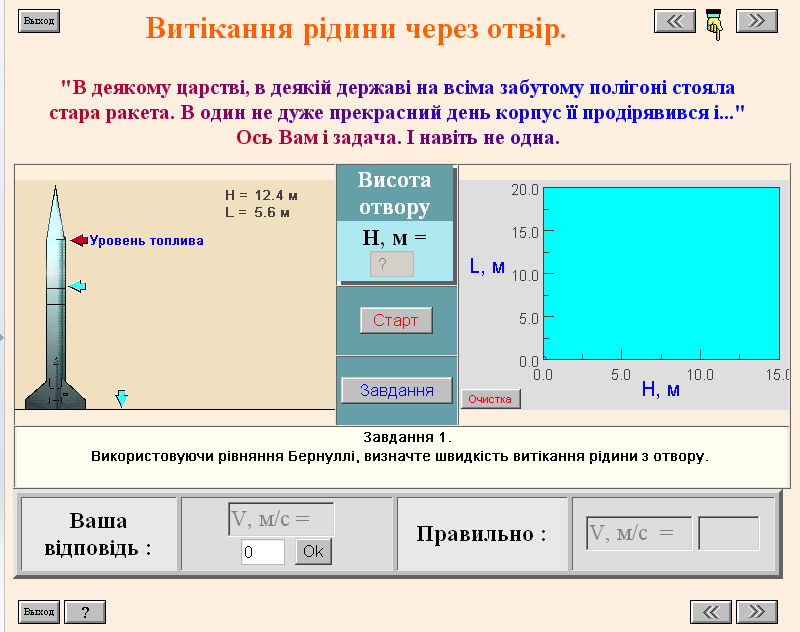
3. Вимiряйте висоту рiвня рiдини в ракетi i зiставте її з даними експериментiв. Контрольні запитання

1. Який рух рідини називається стаціонарним?

2. За яких умов буде справедливим рівняння нерозривності?

3. Запишіть рівняння Бернуллі і поясніть кожну його складову.

4. Від чого і як залежить швидкість витікання рідини із отвору?

5. Що таке ламінарний і турбулентний плин рідини?

6. Від чого залежить динамічна в’язкість і як вона пов’язана із кінематичною в’язкістю?

Література

1. Галущак М.О., Рувінський Б.М. Фізика для інженерів. – Івано-Франківськ: "Факел", 2006.

2. Бушок Г.Ф., Венгер Є.Ф. Курс фізики. Кн.1, 2. – К., ”Либідь“, 2001.

3. Кучерук І.М., Горбачук І.Т., Луцик П.П. Загальний курс фізики. Т.: 1,2,3. – К.: "Техніка", 2001.

4. Галущак М.О. Курс загальної фізики. Кн. 1. – І-Ф.: "Факел", 2000.

5. Савельєв И.В. Курс физики. Т.: 1. – М.: "Наука", 1989.

[1] Ідеальною рідиною називають уявну рідину, у якій відсутні сили внутрішнього тертя.