Уравнение Шрёдингера. Квантование

Плоская волна де-Бройля (3.9) является весьма специальным волновым образованием, соответствующим свободному равномерному движению частицы в определенном направлении и с определенным импульсом. Но частица в силовых полях может совершать и другие движения, описываемые другими волновыми функциями. Основная задача волновой механики как раз и состоит в нахождении волновых функций и связанных с ними физических следствий в разных условиях.

Волновая функция. Уравнение Шрёдингера.

В развитие идеи де-Бройля о волновых свойствах вещества Э.Шрёдингер получил в 1926г. свое знаменитое уравнение. Он сопоставил движению микрочастицы комплексную функцию координат и времени, которую назвал волновой функцией и обозначил греческой буквой 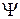. Поэтому ее называют также пси-функцией. Она характеризует состояние микрочастицы. 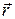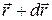Физический смысл волновой функции состоит в следующем: квадрат ее модуля определяет вероятность нахождения частицы в промежутке между точками и в промежуток времени t + dt . Точнее величина 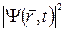является плотностью вероятности или плотностью распределения координат частицы в некотором временном интервале.

Из такого определения следуют свойства волновой функции. Она должна быть однозначной, непрерывной, гладкой (производная не терпит разрыва), конечной. Кроме того, она должна подчиняться условию нормировки .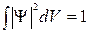

Основная задача физики микрочастиц (волновой или квантовой механики) как раз и состоит в нахождении волновых функций и связанных с ними физических следствий в самых разнообразных условиях. Для ее решения служит волновое уравнение Шрёдингера – основное уравнение нерелятивистской квантовой механики. (Заметим, что одним из решений этого уравнения в свободном пространстве должна быть плоская волна де-Бройля (3.9).)

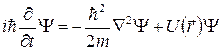(4.1)

Особое значение в квантовой механике имеют стационарные состояния. Это такие состояния, в которых все наблюдаемые физические параметры не меняются с течением времени. Оказывается, что в стационарных состояниях

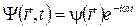, (4.2)

где частота 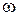постоянна, а функция 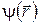не зависит от времени. Эта независящая от времени часть волновой функции может быть найдена из уравнения Шрёдингера для стационарных состояний. В декартовой системе координат оно имеет вид

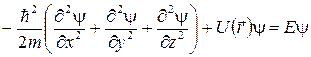, (4.3)

где т - масса частицы, Е – ее энергия, 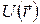- функция, которая в случае стационарных состояний имеет смысл потенциальной энергии частицы.

Энергия частицы Е входит в уравнение в качестве параметра. В теории дифференциальных уравнений доказывается, что уравнения вида (4.3) имеют решения, удовлетворяющие стандартным условиям, не при любых значениях параметра Е, а лишь при некоторых избранных значениях. Эти избранные значения называются собственными значениями энергии. Решения (значения волновой функции), соответствующие собственным значениям Е, называются собственными функциями. Совокупность собственных значений называется спектром величины (энергии). Если эта совокупность образует дискретную последовательность, спектр называется дискретным, если же – непрерывную последовательность, спектр непрерывный или сплошной.

Таким образом, из основных положений квантовой механики без каких-либо дополнительных предположений следует квантование (дискретность) энергии.

Частица в бесконечно глубокой потенциальной яме.

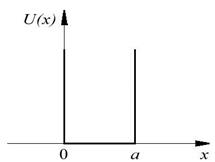
Рассмотрим квантование энергии на простейшем примере движения частицы, находящейся в бесконечно глубокой одномерной потенциальной яме. Пусть частица может двигаться только вдоль оси х, где движение ограничено непроницаемыми для частицы стенками: х = 0 и х =а. Потенциальная энергия равна нулю при 0≤ х ≤а и обращается в бесконечность при х < 0 и x > а .

Поскольку волновая функция в этом случае зависит только от х, уравнение Шрёдингера будет

иметь вид 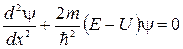. (4.4)

Рис.4.1 За пределы потенциальной ямы частица попасть не может. Поэтому вероятность обнаружить там частицу, а, следовательно, и волновая функция в этих областях равна нулю. Из условия непрерывности следует, что и на границах ямы она равна нулю

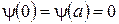. (4.5)

В области, где 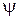не равна тождественно нулю, уравнение (4.4) примет вид 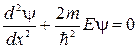. (4.6)

Введя обозначение 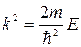, (4.7)

получим уравнение 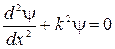, (4.8)

решение которого будет иметь вид

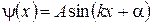. (4.9)

Из первой части условия (4.5) следует 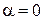. Вторая часть этого условия 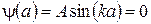будет выполнена лишь в случае, если

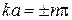(n=1,2,3,…), (4.10)

откуда, приняв во внимание (4.7), найдем собственные значения энергии частицы 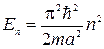(п=1,2,3,…). (4.11)

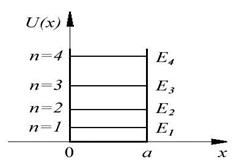Спектр энергии оказался дискретным.

Оценим «расстояния» между соседними уровнями. Разность энергий между двумя соседними уровнями равна

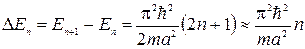. (4.12)

Если оценить эту величину для молекулы газа в

сосуде (т ~ 10 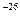кг, а ~ 10cм), получим

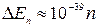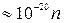Рис.4.2 Дж эВ.

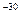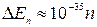Столь густо расположенные энергетические уровни будут практически восприниматься как сплошной спектр энергии, так что, хотя квантование энергии в принципе будет иметь место, на характере движения молекул это сказываться не будет. Аналогичный результат получим, если рассмотреть поведение свободных электронов в металле (те же размеры ямы, т ~ 10 кг, Дж 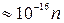эВ). Однако совсем другой результат получится для электрона, если область, в пределах которой он может двигаться, будет порядка атомных размеров (~ 10 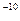м). В этом случае

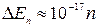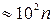Дж эВ,

так что дискретность энергетических уровней будет весьма заметна.

Потенциальные барьеры

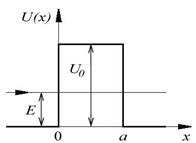
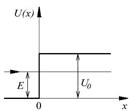Сначала рассмотрим простейший случай – прямоугольный потенциальный барьер, когда потенциальная энергия зависит только от одной координаты х, причем при х = 0 претерпевает скачок (рис.4.3). Пусть слева на границу налетает частица с энергией Е. На языке квантовой теории это означает, что на барьер «падает»

дебройлевская волна .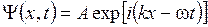

Чтобы удовлетворить граничным условиям при х=0, должна Рис.4.3 существовать как прошедшая волна, так и отраженная.

У этих трех волн частота одна и та же. Поэтому дальше будем говорить только о зависимости .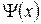

В соответствии с видом 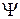−функции для падающей, отраженной и проходящей волны можно найти вероятность для частицы оказаться справа от барьера или отразиться в обратном направлении, а по ним – коэффициенты отражения R и пропускания D (доли частиц отразившихся от барьера или прошедших под барьер).

Здесь возможны два случая.

1. E > 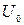. В этом случае можно получить значени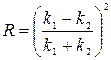е , где 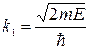; 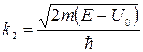. Легко оценить, что при 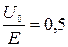получим R = 0,03, т.е. вероятность отражения имеет вполне заметную величину. Заметим, что в классическом случае R = 0.

2. Е < 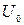. В этом случае коэффициент пропускания D ≠ 0 и можно оценить глубину проникновения под барьер 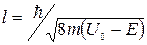. Можно оценить, что при 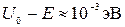глубина проникновения l≈ .

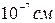В классической физике проникновение частиц под барьер запрещено, поскольку в этой области кинетическая энергия оказалась бы отрицательной, чего быть не может. Но разделение полной энергии на кинетическую и потенциальную не совместимо с соотношением неопределенностей.

Туннельный эффект

Теперь рассмотрим потенциальный барьер конечной ширины (рис.4.4). Решая уравнение Шрёдингера, можно получить для коэффициента пропускания

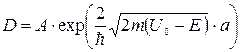, где А – некоторая константа. Например, для ширины барьера 0,1нм (порядка атомных размеров) при 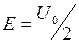получим D≈0,1.

Рис.4.4 Способность квантовых частиц в силу своих волновых свойств заходить под барьер приводит к так называемому туннельному эффекту. Он заключается в следующем. Если частица с энергией Е налетает на потенциальный барьер, то она с определенной вероятностью может пройти сквозь него как бы по туннелю. Туннельный эффект является специфическим квантовым эффектом. Туннельное прохождение сквозь потенциальный барьер лежит в основе многих явлений физики твердого тела (например, явления в контактном

слое на границе двух полупроводников), атомной и ядерной физики (например, α-распад, протекание термоядерных реакций). Например, результаты исследований показывают, что потенциальный барьер при 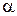- распаде имеет порядок (20 – 30)Мэв, а энергия испущенных 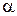- частиц (5 – 6) Мэв, т.е. существенно ниже барьера. Это означает, что 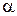- частица испускается только за счет туннельного эффекта.

Гармонический осциллятор

Одной из важных моделей, используемых в атомной физике, является гармонический осциллятор. В атомной и ядерной физике задача о квантовом осцилляторе имеет большое значение. Модель линейного гармонического осциллятора позволяет описать колебания частиц в атомах, атомных ядрах, молекулах, твердых телах.

В квантовой теории понятие силы теряет смысл, поскольку сила по определению является функцией состояния. Но из-за соотношения неопределенностей для микрочастиц о состоянии в классическом смысле нельзя говорить. Поэтому квантовый гармонический осциллятор определяют как поведение частицы массы m, обладающей потенциальной

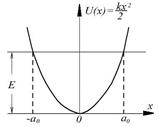
Рис.4.5. энергией такой же, как у классического осциллятора 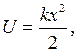где k - постоянная. По аналогии с классическим осциллятором константу k для частицы массы т можно представить 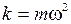. Соответствующая потенциальная кривая есть парабола (рис.4.5). Легко видеть, что эта потенциальная кривая образует нечто вроде ящика с отражающими стенками.

Уравнение Шрёдингера в этом случае будет иметь вид

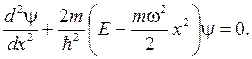(4.13)

Решением данного уравнения являются собственные функции, представляющие собой так называемые полиномы Чебышева – Эрмита, и собственные значения энергии 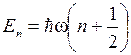(4.14)

Из (4.14) следует, что 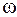имеет смысл циклической частоты фотона, испускаемого или поглощаемого при переходе осциллятора из данного «стационарного» состояния в соседнее.

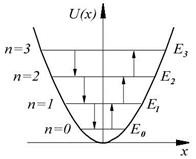Схема соответствующих энергетических уровней приведена на рис.4.6.Видно, что эти уровни эквидистантны, т.е. отстоят друг от друга на одинаковую величину. Минимальная энергия 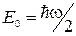. Ее называют нулевой энергией. То, что минимальная энергия не равна нулю, связано с принципом неопределенности. Если бы энергия частицы была равна нулю, то частица покоилась бы, и ее импульс и координаты имели бы одновременно определенные значения, что противоречит принципу неопределенности. Более детальный расчет, выходящий за рамки уравнения Шрёдингера, показывает, что для квантового осциллятора возможны переходы лишь между соседними «стационарными» уровнями, Рис.4.6 при которых квантовое число п изменяется на единицу

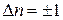. (4.14)

Это условие называют правилом отбора для квантового гармонического осциллятора. При каждом из этих переходов испускается или поглощается фотон с энергией 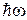, где 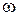- его циклическая частота. (Говорить, что в стационарном состоянии квантовый осциллятор совершает колебания с частотой 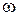неверно. Мы можем говорить лишь о распределении плотности вероятности местоположения частицы.)

Лекция 5