Молекулярно-кинетической теории

Идеальных газов

Для вывода основного уравнения молекулярно-кинетической теории рассмотрим одно атомный идеальный газ. Предположим, что молекулы газа движутся хаотически, число взаимных столкновений между молекулами газа пренебрежимо мало по сравнению с числом ударов о стенки сосуда, а соударения молекул со стенками сосуда абсолютно упругие. Выделим на стенке сосуда некоторую элементарную площадку DS (рис. 64) и вычислим давление, оказываемое на эту площадку. При каждом соударении молекула, движущаяся перпендикулярно площадке, передает ей импульс m₀v - (- т₀) = 2т₀v, где m₀ — масса молекулы, v — ее скорость. За время Dt площадки DS достигнут только те молекулы, которые заключены в объеме цилиндра с основанием DS и высотой vDt (рис. 64). Число этих молекул равно nDSvDt (n— концентрация молекул).

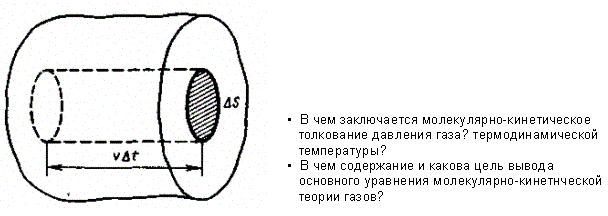
Рис. 64

Необходимо, однако, учитывать, что реально молекулы движутся к площадке DS под разными углами и имеют различные скорости, причем скорость молекул при каждом соударении меняется. Для упрощения расчетов хаотическое движение молекул заменяют движением вдоль трех взаимно перпендикулярных направлений, так что в любой момент времени вдоль каждого из них движется 1/3 молекул, причем половина молекул - 1/6 - движется вдоль данного направления в одну сторону, половина — в противоположную. Тогда число ударов молекул, движущихся в заданном направлении, о площадку DS будет

^l/₆ nDSvDt. При столкновении с площадкой эти молекулы передадут ей импульс

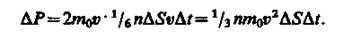
Тогда давление газа, оказываемое им на стенку сосуда,

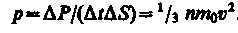(43.1)

Если газ в объеме V содержит N молекул, движущихся со скоростями v₁,v₂, ..., v_n, то целесообразно рассматривать среднюю квадратичную скорость

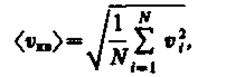(43.2)

характеризующую всю совокупность молекул таза. Уравнение (43.1) с учетом (43.2) примет вид

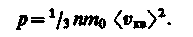(43.3)

Выражение (43.3) называется основным уравнением молекулярно-кинетнческой теории идеальных газов. Точный расчет с учетом движения молекул по всевозможным направлениям дает ту же формулу.

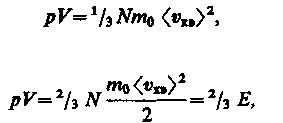(43.4) (43.5)

или

Учитывая, что n=N/V, получим

где Е — суммарная кинетическая энергия поступательного движения всех молекул газа.

Так как масса газа m=Nm₀, то уравнение (43.4) можно переписать в виде

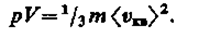
Для одного моля газа т = М (М — молярная масса), поэтому

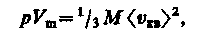
где F_m — молярный объем. С другой стороны, по уравнению Клапейрона — Менделеева, pV_m = RT. Таким образом,

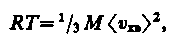
откуда

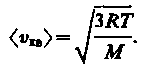(43.6)

Так как M = m₀N_A — масса одной молекулы, а N_А — постоянная Авогадро, то из уравнения (43.6) следует, что

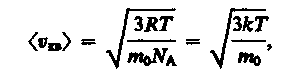(43.7)

где k=R/N_A— постоянная Больцмана. Отсюда найдем, что при комнатной температуре молекулы кислорода имеют среднюю квадратичную скорость 480 м/с, водорода — 1900 м/с. При температуре жидкого гелия те же скорости будут соответственно 40 и 160 м/с.

Средняя кинетическая энергия поступательного движения одной молекулы идеального газа

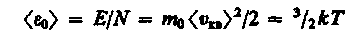(43.8)

(использовали формулы (43.5) и (43.7)) пропорциональна термодинамической температуре и зависит только от нее. Из этого уравнения следует, что при Т=0 <e₀> = 0, т. е. при 0 К прекращается поступательное движение молекул газа, а следовательно, его давление равно нулю. Таким образом, термодинамическая температура является мерой средней кинетической энергии поступательного движения молекул идеального газа, и формула (43.8) раскрывает молекулярно-кинетическое толкование температуры.