Свойства частиц и взаимодействий 4 страница

Используя (1.5-1.6) и (2.2), вычислим величину энергии реакции:

= =

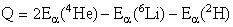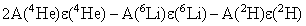= 247.08 - 65.33 -21.11 = 22.44 МэВ.

Реакция является эндотермической.

4. Определить пороги T_пор реакций фоторасщепления ¹²С.

1. + ¹²С ¹¹С + n
2. + ¹²С ¹¹В + р
3. + ¹⁴С ¹²С + n + n

Рассчитаем энергии реакций 1) - 3), используя табличные данные по избыткам масс атомов

1) Q = 0 - (8.071+10.650) = -18.721 МэВ
2) Q = 0 - (8.668 + 7.289) = -15.957 МэВ
3) Q = 3.02 - (0 + 28.071) = -13.122 МэВ
Для пороговой энергии (2.14) можно записать: T_пор 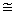Q
так как для реакций 1) - 3) 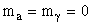и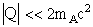

5. Определить пороги реакций: ⁷Li(p, )⁴He и ⁷Li(p, )⁸Be.

Рассчитаем энергии реакций:

1) ⁷Li(p, )⁴He Q = +17.348 МэВ

2) ⁷Li(p, )⁸Be Q = +17.26

Реакции 1) - 2) экзотермические, идут при любых энергиях протонов.

6. Энергия реакции: 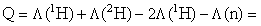13.136 -7.289 - 8.071 = -2.224 МэВ

Так как 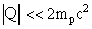, используя выражение (2.14a), получим

E_min =T_пор = 2.224(1 + 0.5) = 3.34 МэВ.

7. Возможны ли реакции:

1. + ⁷Li ¹⁰B+n;
2. + ¹²C ¹⁴N + d

под действием -частиц с кинетической энергией T = 10 МэВ?

Пороги реакций:

1) + ⁷Li ¹⁰B + n
Q = 2.424 + 14.907 - 12.05 - 8.071 = -2.79 МэВ
T_пор = 2.79(1 + 4/7) = 4.38 МэВ
Реакция возможна, т.к. T =10 МэВ > T_пор
2) + ¹²C ¹⁴N + d
Q = 2.424 + 0 - 2.863 - 13.136 = -13.575 МэВ
E_пор = 18.1 МэВ
Реакция невозможна , т.к. T < T _пор.

8. Идентифицировать частицу X и рассчитать энергии реакции Q в следующих случаях:

1. 35Сl + X 32S + ;	4. 23Na + p 20Ne + X;
2. 10B + X 7Li + ;	5. 23Na + d 24Mg + X;
3. 7Li + X 7Be + n;	6. 23Na + d 24Na + X.

Для того чтобы идентифицировать частицу X, нужно использовать законы сохранения заряда и числа нуклонов.

	35Cl	X	32S		Q = -29.013+7.289-(-26.016+2.424) =1.87 МэВ
Z					Реакция экзотермическая
A
		X =p
	10B	X	7Li		Q = 12.05+8.071-(14.907+2.424) =2.79 МэВ
Z					Реакция экзотермическая
A
		X =n
	7Li	X	7Be	n	Q = 14.907+7.29-(15.768+8.07) = -1.643 МэВ
Z					Реакция эндотермическая
A					(Tпор = 1.643(1+1/7) = 1.88 МэВ)
		X =p
	23Na	p	20Ne	X	Q = -9.532+7.289-(-7.041+2.424) = 2.38 МэВ
Z					Реакция экзотермическая
A
				X =
	23Na	d	24Mg	X	Q = -9.532+13.136-(-13.933+8.071) = 9.47 МэВ
Z					Реакция экзотермическая
A
				X = n
	23Na	d	24Na	X	Q = -9.532+13.136-(-8.42+7.289) = 4.74 МэВ
Z					Реакция экзотермическая
A
				X = p

9. Какую минимальную энергию T_min должен иметь дейтрон, чтобы в результате неупругого рассеяния на ядре ¹⁰B возбудить состояние с энергией E_возб = 1.75 МэВ?

При неупругом рассеянии энергия реакции Q = - E_возб., а минимальная энергия дейтрона равняется порогу реакции: T_min = T_пор.

Воспользовавшись формулой для порога реакции (2.14a) (т.к. Q<<m_dc²) получим:

T_min 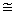E_возб(1+m₁/m₂) 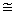1.75(1+2/10) = 2.1 МэВ.

10. Вычислить порог реакции: ¹⁴N + ¹⁷О + p, в двух случаях, если налетающей частицей является:
1) -частица, 2) ядро ¹⁴N. Энергия реакции Q = 1.18 МэВ. Объяснить результат.

Вычислим порог, воcпользовавшись выражением (2.14a):
1) T_пор = 1.18(1 + 4/14) = 1.52 МэВ.
2) T_пор = 1.18(1 + 14/4) = 5.31 МэВ,
В первом случае на движение центра инерции " бесполезно" тратится (4/14)Q, во втором (14/4)Q, таким образом порог реакции во втором случае выше в 3.5 раза.

11. Рассчитать энергии и пороги следующих реакций:

1. d( p, )3He;	5. 32S( ,p )31P;
2. d( d,3He )n;	6.32 ( ,n )31S;
3. 7Li( p,n )7Be;	7. 32S( , )28Si;
4. 3He( , )7Be;	8. 4He( ,p)7Li;

Для расчета энергии и порогов реакций воспользуемся формулами (2.2) и (2.14) и данными таблицы характеристик атомных ядер:

	Реакция	Q (МэВ)	Tпор (МэВ)
	d(p, )3He	+5.494	реакция экзотермическая
	d(d,3He)n	+3.27	реакция экзотермическая
	7Li(p,n)7Be	-1.643	Tпор = 1.88 МэВ
	3He( , )7Be	+1.587	реакция экзотермическая
	32S( ,p)31P	-8.864	Tпор= Q0 (так как m1=0, Q0 << 1)
	32S( ,n)31S	-15.042	Tпор = Q0
	32S( , )28Si	-6.948	Tпор = Q0
	4He( ,p)7Li	-17.34	Tпор 34.68 МэВ

12. Какие ядра могут образовываться в результате реакций под действием : 1) протонов с энергией 10 МэВ на мишени из ⁷Li; 2 )ядер ⁷Li с энергией 10 МэВ на водородной мишени?

Используя законы сохранения электрического заряда и числа нуклонов выпишем всевозможные реакции взаимодействия протонов с ядрами ⁷Li.

Воспользуемся формулами (2.2) и (2.14) и данными таблицы характеристик ядер. Пороги реакций под действием протонов обозначим Т_пор , под действием ядер ⁷Li - T^*_nop. Энергии и пороги реакций приведены в таблице:

	Реакция	Q(МэВ)	Tпор (МэВ)	T*пор(МэВ)
	7Li+p 4He + 4He	17.348
	7Li+p +8Be	17.255
	7Li+p n+7Be	-1.643	1.88	13.14
	7Li+p p+t+ 4He	-2.467	2.82	19.74
	7Li+p n+3He+ 4He	-3.230	3.69	25.84
	7Li+p 3He+ 5He	-4.125	4.71	33.00
	7Li+p t+5Li	-4.434	5.07	35.47
	7Li+p d+ 6Li	-5.025	5.74	40.2
	7Li+p d+d+4He	-6.5	7.43
	7Li+p p+n+ 6Li	-7.249	8.29	57.99
	7Li+p n+p+d+4He	-8.724	9.97	69.79
	7Li+p p+d+5He	-9.619	10.99	76.95

Под действием протонов с энергией 10 МэВ возможны реакции 1) - 11), то есть образуются ядра ¹H, ²H, ³H, ³He, ⁴He, ⁵Li, ⁶Li, ⁷Be, ⁸Be. Под действием ядер ⁷Li с энергией 10 МэВ возможны только реакции 1) - 2), то есть образуются только ядра ⁴He и ⁸Be.

13. Ядро ⁷LI захватывает медленный нейтрон и испускает -квант. Чему равна энергия -кванта?

Реакция

⁷Li(n, )⁸Li, Q = 2.034 МэВ.

Так как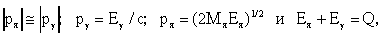

где p_я, 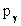- импульсы ядра и -кванта, E_я, 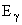- энергии ядра и -кванта, то

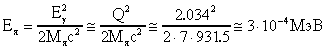
Энергия - -кванта:

E = Q - E_Li 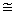Q = 2.034 МэВ

14. Определить в лабораторной системе кинетическую энергию ядра ⁹Ве, образующегося при пороговом значении энергии нейтрона в реакции ¹²C(n, )⁹Be.

Если энергия налетающей частицы равна пороговой энергии, то энергии частиц-продуктов и соответственно их импульсы в с.ц.и. равны нулю. В лабораторной системе импульс ⁹Be 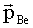равен импульсу переносного движения 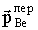(см. (2.19))

.

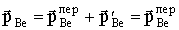Импульс переносного движения 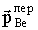выразим через импульс нейтрона (см. (2.22))

.

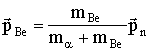Выразим в последнем выражении импульсы через энергии, а затем вместо энергии нейтрона подставим выражение для пороговой энергии, получим

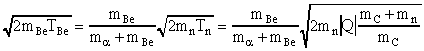
Учитывая, что 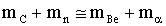, окончательно получим

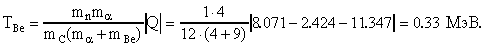
15. При облучении мишени из натурального бора наблюдалось появление радиоактивных изотопов с периодами полураспада 20.4 мин и 0.024 с. Какие образовались изотопы? Какие реакции привели к образованию этих изотопов?

Периоды полураспада 20.4 мин и 0.024 сек соответствуют ядрам ¹¹С, ¹²Ве. Чтобы они образовались под действием одних и тех же частиц пучка, этими частицами должны быть ядра трития или -частицы:

¹¹B(t,2p)¹³Be, ¹¹B(t,3n)¹¹C, ¹¹B(t,2n)¹¹C

или

¹¹B( ,2p)¹³Be, ¹¹B( ,t)¹¹C .

16. Мишень из натурального бора бомбардируется протонами. После окончания облучения детектор 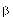-частиц зарегистрировал активность 100 Бк. Через 40 мин активность образца снизилась до ~25 Бк. Каков источник активности? Какая ядерная реакция происходит?

Активность меняется со временем по закону .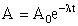

Отсюда находим период полураспада

= 20 мин.

Такой период полураспада имеет ¹¹С, который образуется в реакции ¹¹B(p,n)¹¹C.

17. Воспользуемся формулой (2.30). Для упругого рассеяния

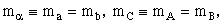( Q = 0). Получим

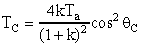
где 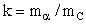, 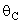- угол вылета ядра ¹²C. Из условия задачи 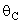= 180⁰. Окончательно имеем

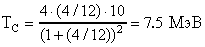
18. Определить максимальную и минимальную энергии ядер ⁷Ве, образующихся в реакции ⁷Li(p,n)⁷Be
(Q = -1,65 МэВ) под действием ускоренных протонов с энергией T_p = 5 МэВ.

Воспользуемся формулой (2.30)

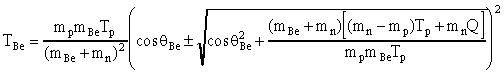
Если второе слагаемое под корнем отрицательно, то диапазон углов ограничивается условием неотрицательности выражения под корнем, т.е.

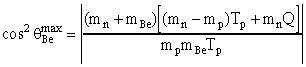
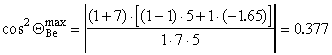
Под корнем будет неотрицательная величина, когда cos 0.614, т.е. максимальный угол, под которым будут вылетать ядра ⁷Be ~52⁰. Кинетическая энергия ядер ⁷Be, вылетающих под этим углом

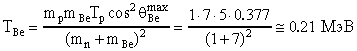
При углах вылета в диапазоне от 0⁰ до 52⁰ ядра ⁷Be могут иметь два значения энергии. Одно из них соответствует знаку "+" перед корнем, а другое знаку "-". Максимальное и минимальное значения кинетической энергии будет при 0⁰:

,

.

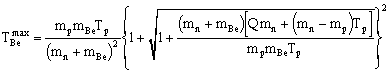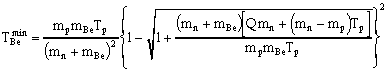Подставляя численные значения, получим

, .

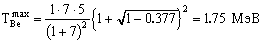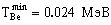Когда ядро ⁷Be вылетает с максимальной энергией, угол вылета нейтрона 180⁰, при минимальной энергии ⁷Be, угол вылета нейтрона 0⁰.

19. -Частицы, вылетающие под углом _неупр = 30⁰ в результате реакции неупругого рассеяния с возбуждением состояния ядра ¹²C с энергией E_возб = 4.44 МэВ, имеют такую же энергию в л.с., что и упруго рассеянные на том же ядре -частицы под углом _упр = 45⁰. Определить энергию -частиц, падающих на мишень .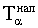

В случае упругого рассеяния энергия -частиц определяется соотношением:

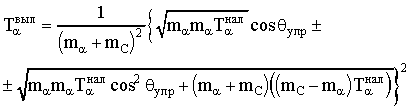, (19.1)

а в случае неупругого:

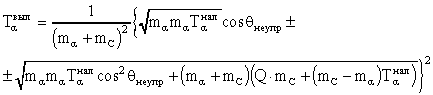, (19.2)

где Q = E_возб.

Приравнивая (19.1) и (19.2), получаем:

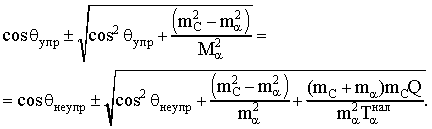
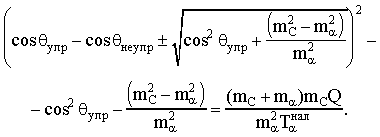
Подставим числовые значения:

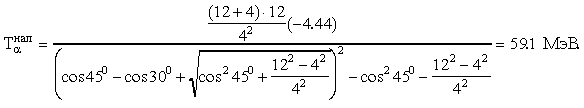
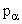20. -Частицы с энергией T = 5 МэВ взаимодействуют с неподвижным ядром ⁷Li. Определить величины импульсов в с.ц.и., образующихся в результате реакции ⁷Li( ,n)¹⁰B нейтрона и ядра ¹⁰B p_Be.

Расчитаем энергию реакции:

Q = 2.424 МэВ + 14.907 МэВ - 8.071 МэВ - 12.050 МэВ = -2.79 МэВ.

Для вычисления кинетической энергии нейтрона и ядра ¹⁰B в с.ц.и. воспользуемся формулой (2.32):

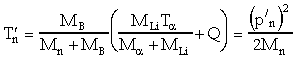
Отсюда в с.ц.и.:

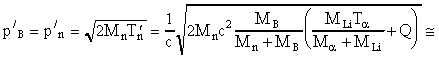
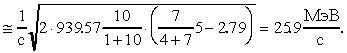
21. С помощью реакции ³²S( ,p)³⁵Cl исследуются низколежащие возбужденные состояния ³⁵Cl (1.219; 1.763; 2.646; 2.694; 3.003; 3.163 МэВ). Какие из этих состояний будут возбуждаться на пучке -частиц с энергией 5.0 МэВ? Определить энергии протонов, наблюдаемых в этой реакции под углами 0⁰ и 90⁰ при Е =5.0 МэВ.

Энергия реакции:

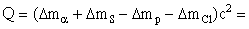
= 2.424 - 26.016 -7.289 + 29.013 = -1.868 МэВ.

Кинетическая энергия столкновения двух частиц в с.ц.и.:

.

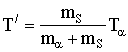Максимальная энергия возбуждения ядра:

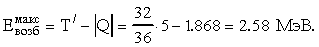
Т.е. при энергии налетающих -частиц 5 МэВ могут возбуждаться только состояния с 1.219, 1.763. Энергии протонов, вылетающих под углами 0⁰ и 90⁰ в реакции определются соотношениями:

,

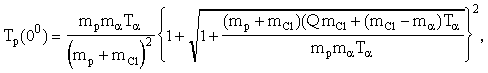
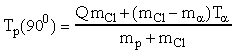где энергия реакции Q = Q₀ - E_возб;

Q₁ = -3.09 МэВ, Q₂ = -3.63 МэВ.

Подставляя численные значения, получим

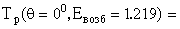
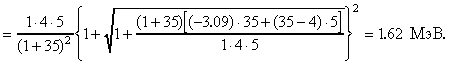
Аналогично для других случаев

Энергия возбуждения (МэВ)	Tp(00) (МэВ)	Tp(900) (МэВ)
1.219	1.62	1.3
1.763	1.03	0.78

22. Используя импульсную диаграмму получить связь между углами в л.с. и с.ц.и.