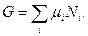Приклади характерних задач з розв’язанням. Задача 1. Довести, що для випадку, коли незалежними змінними системи є температура , тиск і зовнішні параметри крім об’єму
Задача 1. Довести, що для випадку, коли незалежними змінними системи є температура , тиск і зовнішні параметри крім об’єму , термодинамічним потенціалом буде енергія Гіббса, що визначена для простої - системи.
Розв’язання. Відповідно до (6.4) енергія Гіббса простої PV - системи має вигляд:
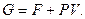 (1)
(1)
З урахуванням (6.3) з (1) знаходимо:
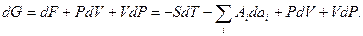 (2)
(2)
Оскільки серед членів суми 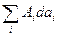 правої частини (2) є доданок вигляду
правої частини (2) є доданок вигляду 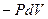 (нехай з номером
(нехай з номером 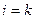 ), після очевидного скорочення отримуємо:
), після очевидного скорочення отримуємо:
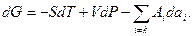
що й потрібно було довести.
Задача 2. Двокомпонентна система знаходиться в термостаті. Виразити хімічний потенціал першого компонента через хімічний потенціал другого для рівноважних ізобаричних процесів.
Розв’язання. Для вказаних умов через те, що 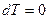 і
і 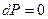 , з рівняння Гіббса-Дюгема (6.28) маємо:
, з рівняння Гіббса-Дюгема (6.28) маємо:
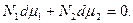 (1)
(1)
Розділивши (1) на 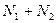 , отримаємо це співвідношення в термінах концентрацій
, отримаємо це співвідношення в термінах концентрацій 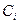 :
:
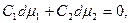 (2)
(2)
де 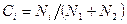 .
.
На підставі зв’язку 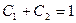 з (2) знайдемо:
з (2) знайдемо:
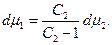 (3)
(3)
Розглядаючи 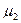 як функцію складу (тобто концентрації
як функцію складу (тобто концентрації 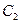 ), перепишемо (2) у вигляді
), перепишемо (2) у вигляді
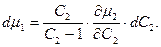 (4)
(4)
Інтегруючи (4), остаточно отримаємо:
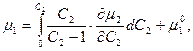 (5)
(5)
де 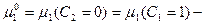 хімічний потенціал чистого першого компонента при заданих
хімічний потенціал чистого першого компонента при заданих 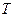 і
і 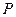 .
.
Задача 3. Визначити клас функцій, що виражають залежність хімічного потенціалу від складу в системах з двох однотипних компонентів.
Розв’язання. Обмежуючись пошуком залежності хімічного потенціалу лише від складу, вважатимемо 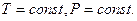 Тоді для двокомпонентної системи з рівняння Гіббса-Дюгема (6.28) маємо (див. попередню задачу):
Тоді для двокомпонентної системи з рівняння Гіббса-Дюгема (6.28) маємо (див. попередню задачу):
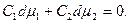 (1)
(1)
У випадку однотипних компонентів з симетрії випливає однакова функціональна залежність 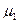 від
від 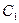 і
і 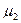 від
від 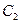 . Отже, вважаючи
. Отже, вважаючи 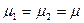 , перепишемо (1) у вигляді
, перепишемо (1) у вигляді
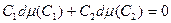
або, симетризуючи,
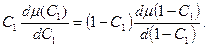 (2)
(2)
Співвідношення (2) можна розглядати як функціональне рівняння вигляду
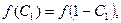 (3)
(3)
де
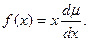 (4)
(4)
Очевидно, що рішенням (3) є будь-яка функція 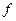 , симетрична відносно значення аргументу
, симетрична відносно значення аргументу 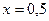 . Загальним виглядом для такої буде
. Загальним виглядом для такої буде
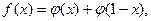 (5)
(5)
де 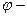 довільна функція.
довільна функція.
Отже, інтегруючи (4) з урахуванням зображення (5), знайдемо шуканий і найбільш загальний в умовах задачі вираз для хімічного потенціалу 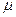 :
:
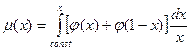 . (6)
. (6)
В остаточному розв’язку (6) необхідно, зрозуміло, обмежитися такими функціями 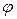 , які визначені на проміжку
, які визначені на проміжку 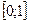 і для яких інтеграл (6) існує в традиційному для фізики рімановому сенсі.
і для яких інтеграл (6) існує в традиційному для фізики рімановому сенсі.
Задача 4. Довести формулу(6.24).
Розв’язання. Скористаємося властивістю потенціалу Гіббса 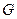 , відповідно до якої він є адитивною функцією кількостей
, відповідно до якої він є адитивною функцією кількостей 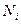 частинок змішаних речовин. Математично це означає, що
частинок змішаних речовин. Математично це означає, що 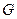 є однорідна функція першого степеня змінних
є однорідна функція першого степеня змінних 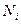 . Звідси на підставі (1.14) можна записати:
. Звідси на підставі (1.14) можна записати:
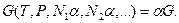 (1)
(1)
Диференціюючи рівність (1) за 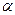 , знайдемо
, знайдемо
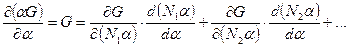 . (2)
. (2)
Вважаючи в (2) 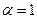 , матимемо
, матимемо
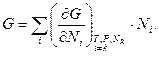 (3)
(3)
Використовуючи (6.16), остаточно отримаємо з (3) шукану рівність: