Задачи для контрольных работ 1 страница

1.1Точка движется по окружности радиусом R = 4 м. Закон ее движения выражается уравнением s = A + Bt², где A = 8 м, B = –2 м/с². Определить момент времени, когда нормальное ускорение a_n точки равно 9 м/с². Найти скорость v, тангенциальное a_t и полное a ускорение точки в тот же момент времени.

1.2Две материальные точки движутся согласно уравнениям и , где A₁ = 4 м/с, B₁ = 8 м/с², С₁ = = –16 м/с³, A₂ = 2 м/с, B₂ = –4 м/с², С₂ = 1 м/с³. В какой момент времени ускорения этих точек будут одинаковы? Найти скорости v₁ и v₂ точек в этот момент времени.

1.3Тело брошено вертикально вверх с начальной скоростью v₀ = 4 м/с. Когда оно достигло верхней точки полета из того же начального пункта, с той же начальной скоростью v₀ вертикально вверх брошено второе тело. На каком расстоянии h от начального пункта встретятся тела? Сопротивление воздуха не учитывать.

1.4Материальная точка движется прямолинейно с ускорением a = 5 м/с². Определить, на сколько путь, пройденный точкой в n-ю секунду, будет больше пути, пройденного в предыдущую секунду. Принять v₀ = 0.

1.5Две автомашины движутся по дорогам, угол между которыми α = 60°. Скорость автомашин v₁ = 54 км/ч и v₂ =72 км/ч. С какой скоростью v удаляются машины одна от другой?

1.6Материальная точка движется прямолинейно с начальной скоростью v₀ = 10 м/с и постоянным ускорением a = –5 м/с. Определить, во сколько раз путь Δs, пройденный материальной точкой, будет превышать модуль ее перемещения Δr спустя t = 5 с после начала отсчета времени.

1.7Точка движется по кривой согласно уравнению ? в котором все величины заданы в единицах СИ. Найти среднюю скорость движения точки в промежутке времени от t₁ = 2 с до t₂ = 6 с.

1.8Велосипедист ехал из одного пункта в другой. Первую треть пути он проехал со скоростьюv₁ = 18 км/ч. Далее половину оставшегося пути он ехал со скоростью v₂ = 22 км/ч, после чего до конечного пункта он шел пешком со скоростью v₃ = 5 км/ч. Определить среднюю скорость <v> велосипедиста.

1.9Первую половину времени автомобиль двигался со скоростью v₁ = 20 м/с под углом a₁ = 60° к заданному направлению, а вторую – под углом a₂ = 120° со скоростью v₂ = 40 м/с. Найти среднюю скорость автомобиля на всем перемещении.

1.10Тело брошено под углом α = 30° к горизонту со скоростью v₀ = 30 м/с. Каковы будут нормальные a_n и тангенциальные a ускорения тела через время t=1 c после начала движения?

1.11Материальная точка движения по окружности с постоянной угловой скоростью ω = π/6 рад/с. Во сколько раз путь Δs, пройденный точкой за время t = 4 с, будет больше модуля ее перемещения Δr? Принять, что в момент отсчета времени радиус – вектор r, задающий положение точки на окружности, относительно исходного положения был повернут на угол φ₀=π/3 рад.

1.12Материальная точка движется в плоскости xy согласно уравнениям x =A₁+B₁t+C₁t² и y=A₂+B₂t+C₂t², где B₁=7 м/с, С₁= –2 м/с, В₂= –1 м/с, С₂=0,2 м/с². Найти модули скорости и ускорения точки в момент времени t = 5 с.

1.13По краю равномерно вращающейся с угловой скоростью ω = 1 рад/с платформы идет человек и обходит платформу за время t = 9,9 с. Каково наибольшее ускорение a движения человека относительно Земли? Принять радиус платформы R=2 м.

1.14Точка движется по окружности радиусом R=30 см с постоянным угловым ускорением ε. Определить тангенциальное ускорение a точки, если известно, что за время t=4 с она совершила три оборота и в конце третьего оборота ее нормальное ускорение a_n =2,7 м/с².

1.15Маховик вращается равноускоренно. Найти угол a, который составляет вектор полного ускорения 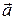любой точки маховика с радиусом в тот момент, когда маховик совершит первые N = 2 оборота.

1.16При горизонтальном полете со скоростью v = 250 м/с снаряд массой m=8 кг разорвался на две части. Большая часть массой m = 6 кг получила скорость v₁ = 400 м/с в направлении полета снаряда. Определить модуль и направление скорости v₂ меньшей части снаряда.

1.17С тележки, свободно движущийся по горизонтальному пути со скоростью v₁ = 3 м/с, в сторону, противоположную движению тележки, прыгает человек, после чего скорость тележки изменилась и стала равной u₁= 4 м/с. Определить горизонтальную составляющую скорости v_2x человека при прыжке относительно тележки. Масса тележки m₁= 210 кг, масса человека m₂ = 70 кг.

1.18Орудие, жестко закрепленное на железнодорожной платформе, производит выстрел вдоль полотна железной дороги под углом α=30° к линии горизонта. Определить скорость u₂ отката платформы, если снаряд вылетает со скоростью u₁= 480 м/с. Масса платформы с орудием и снарядами m₂=18т, масса снаряда m₁ = 60 кг.

1.19Человек массой m₁ = 70 кг, бегущий со скоростью v₁ = 9 км/ч, догоняет тележку массой m₂= 190 кг, движущуюся со скоростью v₂ = 3,6 км/ч, и вскакивает на нее. С какой скоростью станет двигаться тележка с человеком? С какой скоростью будет двигаться тележка с человеком, если человек до прыжка бежал на встречу тележки?

1.20Конькобежец, стоя на коньках на льду, бросает камень массой m₁=2,5 кг под углом α=30° к горизонту со скоростью v =10 м/с. Какова будет начальная скорость v₀ движения конькобежца, если масса его m₂=60 кг? Перемещением конькобежца во время броска пренебречь.

1.21На полу стоит тележка в виде длинной доски, снабженной легкими колесами. На одном конце доски стоит человек. Масса его m₁= 60 кг, масса доски m₂=20 кг. С какой скоростью (относительно пола) будет двигаться тележка, если человек пойдет вдоль нее со скоростью (относительно доски) v = 1 м/с? Массой колес и трением пренебречь.

1.22Снаряд, летевший со скоростью v = 400 м/с, в верхней точке траектории разорвался на два осколка. Меньший осколок, масса которого составляет 40% от массы снаряда, полетел в противоположном направлении со скоростью u₁=150 м/с. Определить скорость u₂ большего осколка.

1.23Две одинаковые лодки массами m=200 кг каждая (вместе с человеком и грузами, находящимися в лодках) движутся параллельными курсами навстречу друг другу с одинаковыми скоростями v = 1 м/с. Когда лодки поравнялись, то с первой лодки на вторую и со второй на первую одновременно перебрасывают грузы массами m₁=20 кг. Определить скорости u₁и u₂ лодок после перебрасывания грузов.

1.24На сколько переместится относительно берега лодка длинной l=3,5 м и массой m₁=200 кг, если стоящий на корме человек массой m₂= 80 кг переместится на нос лодки? Считать лодку расположенной перпендикулярной берегу.

1.25Лодка длинной l=3 м и массой m=120 кг стоит на спокойной воде. На носу и корме находятся два рыбака массами m₁=60 кг и m₂=90 кг. На сколько сдвинется лодка относительно воды, если рыбаки поменяются местами?

1.26В лодке массой M = 240 кг стоит человек массой m = 60 кг. Лодка плывет со скоростью v = 2 м/с.Человек прыгает с лодки в горизонтальном направлении со скоростью u = 4 м/с (относительно лодки). Найти скорость лодки после прыжка человека: 1) вперед по движению; 2) в сторону, противоположную движению лодки.

1.27Человек, стоящий на лодке, сделал шесть шагов вдоль нее и остановился. На сколько шагов передвинулась лодка, если масса лодки в два раза больше (меньше) массы человека?

1.28Тело массы M = 990 г лежит на горизонтальной поверхности. В него попадает пуля массы m = 10 г и застревает в нем. Скорость пули v = 700 м/с и направлена горизонтально. Какой s пройдет тело до остановки? Коэффициент трения между телом и поверхностью k = 0,05.

1.29Падающий вертикально шарик массы m = 200 г ударился об пол со скоростью v = 5 м/с и подпрыгнул на высоту h = 46 см. Найти изменение ∆р импульса шарика при ударе.

1.30Тело массой m₁ = 2 кг движется навстречу второму телу массой m₂ = 1,5 кг и неупруго соударяется с ним. Скорости тел непосредственно перед ударом были v₁ = 1 м/с и v₂ = 2 м/с. Какое время будут двигаться эти тела послу удара, если коэффициент трения k = 0,05?

1.31В деревянный шар массой m₁=8 кг, подвешенный на нити длинной l=1,8 м, попадает горизонтально летящая пуля массой m₂=4 г. С какой скоростью летела пуля, если нить с шаром и застрявшей в нем пулей отклонились от вертикали на угол a=3°? Размером шара пренебречь, удар пули считать прямым, центральным.

1.32По небольшому куску мягкого железа, лежащему на наковальне массой m₁=300 кг, ударяет молот массой m₂=8 кг. Определить КПД h удара, если удар неупругий. Полезной считать энергию, затраченную на деформацию куска железа.

1.33Шар массой m₁=1 кг движется со скоростью v₁ = 4 м/с и сталкивается с шаром массой m₂=2 кг, движущимся навстречу ему со скоростью v₂ = 3 м/с. Каковы скорости u₁ и u₂ шаров после удара? Удар считать абсолютно упругим, прямым, центральным.

1.34Шар массой m₁=3 кг движется со скоростью v₁ = 2 м/с и сталкивается с покоящимся шаром массой m₂=5 кг. Какая работа будет совершена при деформации шаров? Удар считать абсолютно неупругим, прямым, центральным.

1.35Определить КПД η неупругого удара бойка массой m₁=0,5т, падающего на сваю массой m₂=120 кг. Полезной считать энергию, потраченную на вбивание сваи.

1.36Шар массой m₁=4 кг движется со скоростью v₁ = 5 м/с и сталкивается с шаром массой m₂=6 кг, движущимся навстречу ему со скоростью v₂ = 2 м/с. Определить каковы скорости u₁ и u₂ шаров после удара. Удар считать абсолютно упругим, прямым, центральным.

1.37Из ствола автоматического пистолета вылетела пуля массой m₁= 10 г со скоростью v = 300 м/с. Затвор пистолета массой m₂=200 г прижимается пружиной, жесткость которой k=25 кН/м. На какое расстояние отойдет затвор после выстрела? Считать, что пистолет жестко закреплен.

1.38Шар массой m₁=5 кг движется со скоростью v₁ =1 м/с и сталкивается с покоящимся шаром массой m₂=2 кг. Определить каковы скорости u₁ и u₂ шаров после удара. Удар считать абсолютно упругим, прямым, центральным.

1.39Из орудия, не имеющего противооткатного устройства, производилась стрельба в горизонтальном направлении. Когда орудие было неподвижно закреплено, снаряд вылетел со скоростью v₁ = 600 м/с, а когда орудию дали возможность откатываться назад, снаряд вылетел со скоростью v₂ = 580 м/с. С какой скоростью откатилось при этом орудие?

1.40Шар массой m₁=2 кг сталкивается с шаром большей массы и при этом теряет 40% кинетической энергии. Определить массу m₂ большего шара. Удар считать абсолютно упругим, прямым, центральным.

1.41Определить работу растяжения двух соединенных последовательно пружин жесткостями k₁=400 Н/м и k₂=250 Н/м, если первая пружина при этом растянулась на Δl = 2 см.

1.42Из шахты глубиной h = 600 м поднимают клеть массой m₁=3т на канате, каждый метр которого имеет массу m = 1,5 кг. Какая работа А совершается при поднятии клетки на поверхность Земли? Каков коэффициент полезного действия η подъемного устройства?

1.43Пружина жесткостью k=500 Н/м сжата силой F = 100 Н. Определить работу А внешней силы, дополнительно сжимающей пружину еще на Δl = 2 см.

1.44Две пружины жесткостью k₁=0,5 кН/м скреплены параллельно. Определить потенциальную энергию П данной системы при абсолютной деформации Δl = 4 см.

1.45Какую нужно совершить работу А, чтобы пружину жесткостью k = 800 Н/м, сжатую на х = 6 см, дополнительно сжать на Δх = 8 см?

1.46На краю платформы в виде диска, вращающейся по инерции вокруг вертикальной оси с частотой п₁=8 мин^-1 стоит человек массой m₁ = 70 кг. Когда человек перешел в центр платформы, она стала вращаться с частотой n₂ = 10 мин^-1. Определить массу т₂ платформы. Момент инерции человека рассчитывать как для материальной точки.

1.47По касательной к шкиву маховика в виде диска диаметром D = 75 см и массой m = 40 кг приложена сила F = 1 кН. Определить угловое ускорение ε и частоту вращения n маховика через время t = 10 с после начала действия силы, если радиус r шкива равен 12 см. Силой трения пренебречь.

1.48На обод маховика диаметром D = 60 см намотан шнур, к концу которого привязан груз массой m = 2 кг. Определить момент инерции J маховика, если он, вращаясь равноускоренно под действием силы тяжести груза, за время t = 3 с приобрел угловую скорость ω=9 рад/с.

1.49Нить с привязанными к ее концам грузами массами m₁ = 50 г и m₂ = 60 г перекинута через блок диаметром D = 4 см. Определить момент инерции J блока, если под действием силы тяжести грузов он получил угловое ускорение ε = 1,5 рад/с². Трением и проскальзыванием по блоку нити пренебречь.

1.50Стержень вращается вокруг оси, проходящей через его середину, согласно уравнению φ = At+Bt³, где A = 2 рад/с, В = 0,2 рад/с³. Определить вращающий момент М, действующий на стержень через время t =2 с после начала вращения, если момент инерции стержня J = 0,048 кг·м².

1.51По горизонтальной плоскости катиться диск со скоростью v = 8м/с. Определить коэффициент сопротивления, если диск, будучи предоставленным самому себе, остановился пройдя путь s = 18 м.

1.52Определить момент силы M, который необходимо приложить к блоку, вращающемуся с частотой n = 12 с^-¹, чтобы он остановился в течение времени Δt =8 с. Диаметр блока D = 30 см. Массу блока m = 6 кг считать равномерно распределенной по ободу.

1.53Блок, имеющий форму диска массой m=0,4 кг, вращается под действием силы натяжения нити, к концам которой подвешены грузы массами m₁ = 0,3кг и m₂ = 0,7 кг. Определить силы натяжения Т₁ и Т₂ нити по обе стороны блока.

1.54К краю стола прикреплен блок. Через блок перекинута невесомая и нерастяжимая нить, к концам которой прикреплены грузы. Один груз движется по поверхности стола, а другой – вдоль вертикали вниз. Определить коэффициент f трения между поверхностями груза и стола, если массы каждого груза и масса блока одинаковы и грузы движутся с ускорением a = 5,6 м/с². Проскальзыванием нити по блоку и силой трения, действующей на блок, пренебречь.

1.55К концам легкой и нерастяжимой нити, перекинутой через блок подвешены грузы массами m₁= 0,2 кг и m₂ = 0,3 кг. Во сколько раз отличаются силы, действующие на нить по обе стороны от блока, если масса блока m = 0,4 кг, а его ось движется вертикально вверх с ускорением a = 2 м/с²? Силами трения и проскальзыванием нити по блоку пренебречь.

1.56Горизонтальная платформа массой т₁=150 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой п=8 мин^-1. Человек массой т₂=70 кг стоит при этом на краю платформы. С какой угловой скоростью ω начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу круглым, однородным диском, а человека – материальной точкой.

1.57На скамье Жуковского стоит человек и держит стержень вертикально по оси скамьи. Скамья с человеком вращается с угловой скоростью ω₁=4 рад/с. С какой угловой скоростью ω₂ будет вращаться скамья с человеком, если повернуть стержень так, чтобы он занял горизонтальное положение? Суммарный момент вращения человека и скамьи J=5 кг·м². Длинна стержня l=1,8 м, масса m=6 кг. Считать, что центр масс стержня с человеком находится на оси платформы.

1.58Платформа в виде диска диаметром D=3 м и массой m₁=180 кг может вращаться вокруг вертикальной оси. С какой угловой скоростью будет вращаться эта платформа, если по ее краю пойдет человек массой m₂=70 кг со скоростью v = 1,8 м/с относительно платформы?

1.59Платформа, имеющая форму диска, может вращаться около вертикальной оси. На краю платформы стоит человек. На какой угол φ повернется платформа, если человек пойдет вдоль края платформы и, обойдя ее, вернется в исходную (на платформе точку) точку? Масса платформы m₁=280 кг, масса человека m₂=80 кг.

1.60На скамье Жуковского стоит человек и держит в руке за ось велосипедное колесо, вращающееся вокруг своей оси с угловой скоростью ω₁=25 рад/с. Ось колеса расположена вертикально и совпадает с осью скамьи Жуковского. С какой скоростью ω₂ станет вращаться скамья, если повернуть колесо вокруг горизонтальной оси на угол a=90°? Момент инерции человека и скамьи J равен 2,5 кг×м², момент инерции колеса J₀=0,5 кг×м².

1.61Определить напряжение G гравитационного поля на высоте h=1000 км над поверхностью Земли. Считать известным ускорение g свободного падения у поверхности Земли и ее радиус R.

1.62Какая работа А будет совершена силами гравитационного поля при падении на Землю тела массой т=2 кг: 1) с высоты h=1000 км; 2) из бесконечности?

1.63Из бесконечности на поверхность Земли падает метеорит массой т=30 кг. Определить работу А, которая при этом будет совершена силами гравитационного поля Земли. Ускорение свободного падения g у поверхности Земли и ее радиус считать известными.

1.64С поверхности Земли вертикально вверх пущена ракета со скоростью v = 5 км/с. На какую высоту она поднимется?

1.65По круговой орбите вокруг Земли обращается спутник с периодом Т=90 мин. Определить высоту спутника. Ускорение свободного падения g у поверхности Земли и ее радиус считать известными.

1.66На каком расстоянии от центра Земли находится точка, в которой напряженность суммарного гравитационного поля Земли и Луны равна нулю? Принять, что масса Земли в 81 раз больше массы Луны и что расстояние от центра Земли до центра Луны равно 60 радиусам Земли.

1.67Спутник обращается вокруг Земли по круговой орбите на высоте h=520 км. Определить период обращения спутника. Ускорение свободного падения g у поверхности Земли и ее радиус считать известными.

1.68Определить линейную и угловую скорости спутника Земли, обращающегося по круговой орбите на высоте h=1000 км. Ускорение свободного падения g у поверхности Земли и ее радиус считать известными.

1.69Какова масса Земли, если известно, что Луна в течение года совершает 13 обращений вокруг Земли и расстояние от Земли до Луны равно 3,84×10⁸ м?

1.70Во сколько раз средняя плотность земного вещества отличается от средней плотности лунного? Принять, что радиус R_з Земли в 390 раз больше радиуса R_л Луны и вес тела на Луне в 6 раз меньше веса тела на Земле.

1.71Звездная система состоит из двух одинаковых звезд, находящихся на расстоянии r = м друг от друга. Найти период Т обращения звезд вокруг общего центра масс, если масса каждой звезды m = кг.

1.72Искусственный спутник обращается вокруг Земли по круговой орбите на высоте H = 3200 км над поверхностью Земли. Определить линейную скорость спутника.

1.73На какую часть уменьшается вес тела на экваторе вследствие вращения Земли вокруг оси?

1.74Три материальных точки массой m расположены в вершинах правильного треугольника, сторона которого равна a. Найти гравитационную силу, действующую на одну из масс со стороны двух других.

1.75Спутник, движущийся по круговой орбите радиуса R = 2×10⁴ км в экваториальной плоскости Земли с Запада на Восток, появляется над некоторым пунктом на экваторе через каждые t = 11,6 ч. Вычислить на сновании этих данных массу Земли. Гравитационная постоянная предполагается известной.

1.76На стержне длиной l=30 см укреплены два одинаковых грузика: один – в середине стержня, другой – на одном из его концов. Стержень с грузами колеблется около горизонтальной оси, проходящей через свободный конец стержня. Определить приведенную длину L и период Т простых гармонических колебаний данного физического маятника. Массой стержня пренебречь.

1.77Точка участвует в двух взаимно перпендикулярных колебаниях, уравнения которых x=A₁sin ω₁t и y=A₂cos ω₂t, где A₁=8 см, A₂=4 см, ω₁ = = ω₂= 2 с^-1. Написать уравнение траектории и построить ее. Показать направление движения точки.

1.78Точка совершает простые гармонические колебания, уравнение которых x=A sinωt , где А=5 см, ω=2 с^-1. В момент времени, когда точка обладала потенциальной энергией E_p=0,1 мН, на нее действовала возвращающая сила F = 5 мН. Найти этот момент времени t.

1.79Определить частоту простых гармонических колебаний диска радиусом R=20 см около горизонтальной оси, проходящей через середину радиуса диска перпендикулярно его плоскости.

1.80Определить период Т простых гармонических колебаний диска радиусом R=40 см около горизонтальной оси, проходящей через образующую диска.

1.81Определить период Т колебаний математического маятника, если его модуль максимального перемещения ∆r=18 см и максимальная скорость v_max = 16 см/с.

1.82Материальная точка совершает простые гармонические колебания так, что в начальный момент времени смещение x₀=4 см, а скорость v₀ = 10 см/с. Определить амплитуду А и начальную фазу колебаний, если их период Т=2 с.

1.83Складываются два колебания одинакового направления и одинакового периода: x₁=A₁sin ω₁t и х₂=A₂sin ω₂(t+ ), где A₁=A₂=3 см, ω₁=ω₂= с^-1, =0,5 с. Определить амплитуду А и начальную фазу результирующего колебания. Написать его уравнение. Построить векторную диаграмму для момента времени t=0.

1.84На гладком горизонтальном столе лежит шар массой М=200 г, прикрепленный к горизонтально расположенной легкой пружине с жесткостью k=500 Н/м. В шар попадает пуля массой т=10 г, летящая со скоростью v = 300 м/с, и застревает в нем. Пренебрегая перемещением шара во время удара и сопротивлением воздуха, определить амплитуду А и период Т колебаний шара.

1.85Шарик массой т=60 г колеблется с периодом Т=2 с. В начальный момент времени смещение шарика х₀=4,0 см и он обладает энергией Е =0,02 Дж. Записать уравнение простого гармонического колебания шарика и закон сохранения возвращающей силы с течением времени.

1.86Точка совершает гармонические колебания, уравнение которых имеет вид x = Asinωt, где A = 5 см, w = 2 с^–1. Найти ближайший момент времени, в который потенциальная энергия очки П = 10^–4 Дж, а возвращающая сила F=+5×10^–3 Н. Определить также фазу колебаний в этот момент времени.