Модели пространственно-временной и поляризационной структуры сигналов

Упомянутые выше сигналы в РИС (зондирующий, сигнал подсве­та, запросный, ответный, собственное радиоизлучение объекта на­блюдения, отраженный сигнал и т.п.) являются электромагнитными по­лями, которые характеризуются временной и пространственной структу­рой. Кроме того, электромагнитное, поле, являясь векторным, в отли­чие, например, от скалярного акустического поля, характеризуется еще и поляризационной структурой. Следовательно, модель сигнала должна отражать его временную, пространственную и поляризационную структуру:

.

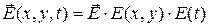Здесь – вектор напряженности электрического (магнитного) поля, в общем случае эллиптически поляризованного (рис. 1.1), который может быть разложен на две ортогонально поляризованные составляющие, каждая из которых характеризуется своей амплитудой и фазой:

,

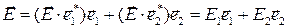где [ 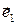, 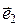] – поляризационный базис – пара ортонормированных векторов 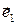и 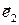единичной длины.

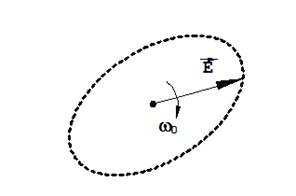
Рис.1.1. Годограф – траектория, описываемая концом вращающегося с угловой скоростью ω₀ вектора напряженности электрического (магнитного) поля элиптически поляризованной волны.

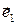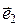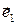E₁, E₂ – комплексные числа (координаты) вектора в базисе [ , ], являющиеся проекциями вектора на направления ортов и 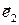соответственно:

.

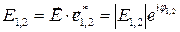Обычно применяемые разложения в базисе из двух линейно поляризован­ных компонент или двух поляризованных по кругу компонент являются лишь частными случаями.

Меняя амплитуды и фазы (управляя амплитудами и фазами) ортого­нально поляризованных колебаний (волн) с линейной поляризацией, получаемых, например, с помощью горизонтально и вертикально расположен­ных вибраторов, или с круговой поляризацией, получаемых, например, с помощью спиральных излучателей с правозаходной или левозаходной спиралью, можно формировать необходимую поляризационную структуру излучаемого сигнала и управлять ею.

В общем случае комплексные амплитуды ортогонально поляризованных колебаний (E₁, E₂)могут быть функциями времени, и том числе случайными. При этом поляризационный эллипс (его форма и ориентация) меняется во времени. При случайном характере комплексных амплитуд поляризационный эллипс размывается, причем степень его размытости определяется степенью коррелированности случайных амплитуд E₁(t) и E₂(t) (рис. 1.2).

При независимых комплексных амплитудах электромагнитная вол­на становится хаотически поляризованной (рис. 1.3).

Рис. 1.2. Поляризационная структура электромагнитного поля при случайных коррелированных комплексных амплитудах ортогонально поляризованных составляющих.

Рис.1.3. Поляризационная структура электромагнитного поля при независимых комплексных амплитудах ортогонально поляризованных составляющих.

Пространственная структура сигнала описывается амплитудно-фазовым распределением поля на раскрыве антенной системы (передаю­щей или приемной)

,

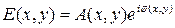где x, y – координаты раскрыва антенны.

Наиболее часто используемыми амплитудными и фазовыми распре­делениями поля на раскрыве антенны являются:

- амплитудное равномерное распределение (рис. 1.4)

, , ,

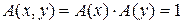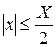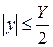где X, Y - размеры раскрыва;

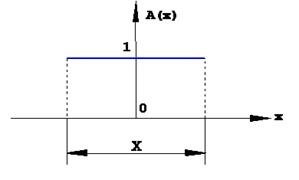
Рис.1.4. Амплитудное равномерное распределение поля на раскрыве антенны

- амплитудное колоколообразное (гауссово) распределение (рис. 1.5)

,

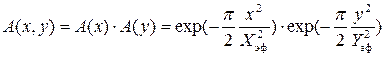где X_эф, Y_эф – эффективный раскрыв антенны, удовлетворяющий условию

;

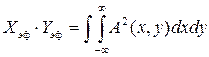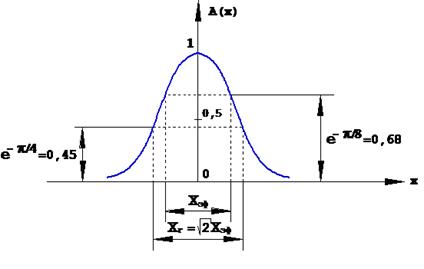
Рис.1.5. Амплитудное колоколообразное (гауссово) распределение поля на раскрыве антенны.

- амплитудное косинусоидальное распределение m-й степени (рис. 1.6)

, , ,

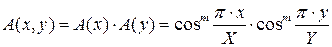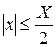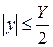причем

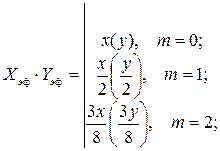
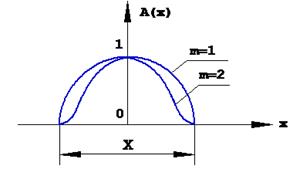
Рис. 1.6. Амплитудное косинусоидальное распределение поля на раскрыве антенны (первой и второй степени)

- фазовое равномерное распределение, соответствующее не наклоненному плоскому волновому фронту (рис 1.7)

, , ,

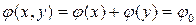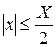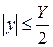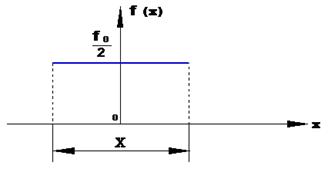
Рис. 1.7. Фазовое равномерное распределение поля на раскрыве антенны, соответствующее ненаклонному плоскому волновому фронту.

- фазовое линейное распределение, соответствующее наклоненному плоскому волновому фронту (рис. 1.8)

,

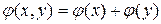причем согласно рис. 1.8

,

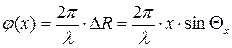аналогично

;

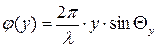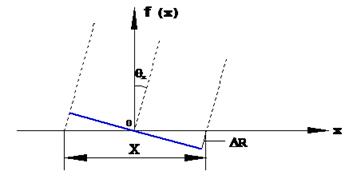
Рис.1.8. Фазовое равномерное распределение поля на раскрыве антенны, соответствующее наклонному плоскому волновому фронту.

- фазовое квадратичное распределение, соответствующее сферическому волновому фронту (рис. 1.9)

,

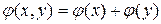причем согласно рис. 1. 9

,

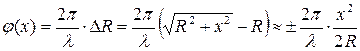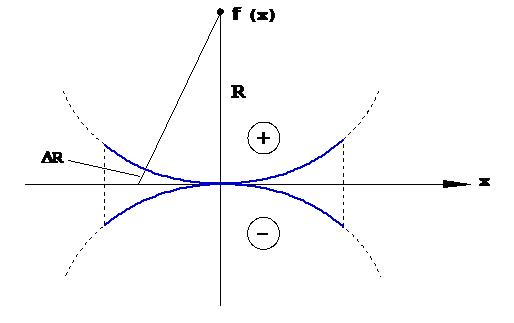
Рис.1.9. Фазовое квадратичное распределение поля на раскрыве антенны, соответствующее сферическому волновому фронту.

аналогично

,

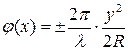где R – радиус сферического волнового фронта, знак "±" соот­ветствует положению сферического фронта относительно раскрыва антенны.

В общем случае амплитудно-фазовое распределение поля на раскрыве антенны может быть не только детерминированным, но и случайным что подробно будет рассмотрено при изложении вопросов пространственной обработки сигналов.

Временная структура сигнала характеризуется амплитудно-фазовыми законами регулярной U(t) и случайной M(t) модуляции:

.

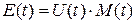Регулярная модель отражает первичную амплитудно-фазовую модуляцию при формировании сигнала, а случайная модель, как правило, отражает вторичную амплитудно-фазовую модуляцию, приобретаемую сигналом в процессе его распространения и отражения:

,

.

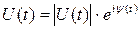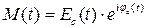Будем считать результатом регулярной модуляции периодическую последовательность N одиночных радиосигналов, каждый из которых характеризуется законом модуляции U₀(t):

,

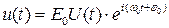причем

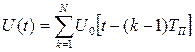
где T_п – период следования (повторения) одиночных сигналов,

E₀, ω₀, φ₀ – амплитуда, частота, начальная фаза одиночных сигналов.