EXAMPLES OF PROBLEM SOLUTION. Example 6. In the middle of the long straight solenoid, which has 10 turns per centimeter, there is the circular contour with area 10 сm2
Example 6. In the middle of the long straight solenoid, which has 10 turns per centimeter, there is the circular contour with area 10 сm2. Plane of contour is situated at an angle of 300 to an axis of the solenoid (look at the picture). A current 5A flows over the winding of solenoid. What average EMF is appears in the circular contour, if during 10 ms the direction of a current in solenoid is changed on the opposite one?
| Input data: n0 = 10 cm –1 = 103 m–1 S = 10 cm 2 = 10 –3 m 2; j = 30 0; І =5А; Dt = 10 ms = 10 –2 s. | 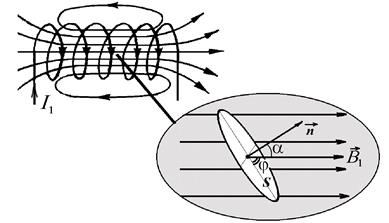 |
Find: 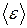 – ? – ? |
Solution: When a current in the coil of solenoid is changed, the magnetic flux of F, that runs through the circular contour, will change too. EMF of induction, which can be found in Faraday's law of electromagnetic induction e = –df/ dt appears owing to this in contour. They find instantaneous value of EMF of induction with this formula, but for finding the average value from the average speed of magnetic flux changing in course of time we should write
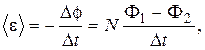 (1)
(1)
where 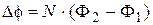 - the interlinkage changing in time interval of Dt. Circular contour has a one loop N=1. In the middle part of long solenoid field will be homogeneous. In this case the magnetic flux is found with the formula: Ф=BS× cosa, where В – the solenoid magnetic field induction; S – area of contour; α = 900–j – angle between vector
- the interlinkage changing in time interval of Dt. Circular contour has a one loop N=1. In the middle part of long solenoid field will be homogeneous. In this case the magnetic flux is found with the formula: Ф=BS× cosa, where В – the solenoid magnetic field induction; S – area of contour; α = 900–j – angle between vector 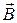 and normal
and normal 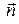 to the plane of contour.
to the plane of contour.
The magnetic field induction is in the middle of long solenoid
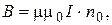 (2)
(2)
where 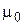 – a magnetic constant; m– magnetic permeability of medium (in air m=1) I – current strength in the winding of solenoid;
– a magnetic constant; m– magnetic permeability of medium (in air m=1) I – current strength in the winding of solenoid; 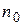 – quantity of turns per the unit of length of a solenoid.
– quantity of turns per the unit of length of a solenoid.
Let’s choose the direction of a current in the winding of solenoid, as it’s shown in the picture I1, and we’ll find corresponding to the direction of vector 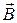 1 with the screw rule. Magnetic flux equals in this case
1 with the screw rule. Magnetic flux equals in this case
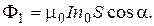 (3)
(3)
After changing the current direction on opposite one and vector of magnetic induction will change its direction 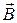 2 ¯
2 ¯ 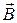 1.
1.
Magnetic Flux
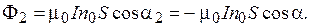 . (4)
. (4)
Here it is necessary to take into account, that a2=1800–a and cosa2= –cosa. Inserting the expressions F1 (3) and F2 (4) in the formula (1) and taking into account, that a=900–j and cosa= –cosj (look at the picture), we get
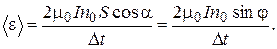
Let’s check if the right part of the calculating formula gives the unity of EMF difference [V]:
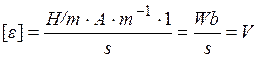
Let’s make the calculations
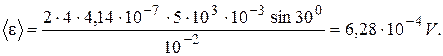
Result: 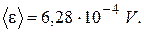
Example 7 In the homogeneous magnetic field with induction of 0,5Т short coil is uniformly rotated. Coil consists of 100 loops with the area of 100 сm2. The axis of rotation is in the plane of loops of the coil and perpendicularly to the lines of magnetic field induction (see the picture).
Find: 1) maximal EMF, which appears into coil with its rotation with period of 0.1 s;
2) charge, which flows over the coil within the change of angle between coil’s axis and magnetic induction’s vector from j1=0o to j2=90o, if the coil resistance is 2W.
Input Data: В=0,5 Т, N=100, S=100 cm  , Т=0,1 s, φ1=0, φ2=90 о , Т=0,1 s, φ1=0, φ2=90 о  | 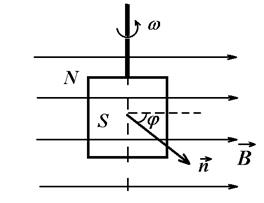 |
| Find: emax ; Q – ? |
Solution: The magnetic flux which runs through the coil changes with the rotation of the coil, and in accordance with Faraday's law of electromagnetic induction in coil EMF of induction appears
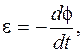 (1)
(1)
where the magnetic flux interlinkage in the homogeneous magnetic field with induction of В is found with the formula:
f=BSN×cosj (2)
where S – area of loops; j – angle between normal 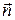 to the plane of coil’s loops and vector
to the plane of coil’s loops and vector 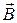 ; N – quantity of loops, which are transpierced with the flux Ф=BS× cosj. Coil during time of t will be turned an angle of j=wt, when the rotation is uniform, w – angular velocity of rotation, which related with the period of rotation as
; N – quantity of loops, which are transpierced with the flux Ф=BS× cosj. Coil during time of t will be turned an angle of j=wt, when the rotation is uniform, w – angular velocity of rotation, which related with the period of rotation as 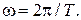
Substituted expressions w and j in the formula (2) we’ll get
f =BSN×coswt = 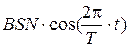 . (3)
. (3)
In order to find the instantaneous value of EMF of induction we’ll substitute the expression for magnetic flux interlinkage (3) in the formula (1) and differentiate with time

The value of EMF will be maximum at that moment of time, if 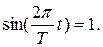
Then  . (4)
. (4)
In order to find the charge of Q, which runs over the coil, let’s apply Ohm's law for a closed circuit instantaneous value of EMF
eI=Ri (5)
where R – coil’s resistance; i– instantaneous value of current in the coil.
Equating the right parts of equations (1) and (5), we’ll get
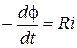
As there is instantaneous value of current strength i=dQ / dt then this equation can be rewritten in the type of

whence
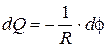 (6)
(6)
If one takes integral from expression (6), then we’ll find charge, which flows through the coil with the change of magnetic flux interlinkage from f1 till f2:
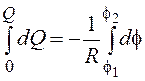 or
or 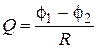 (7)
(7)
Changing the angle between coil’s axis and vector 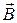 from j1 to j2, then the magnetic flux interlinkage will change from f1=BSN×cosj1 till f2=BSN×cosj2. Substituted expressionsf1 and f2 in the formula (7), we’ll find the sought-for charge:
from j1 to j2, then the magnetic flux interlinkage will change from f1=BSN×cosj1 till f2=BSN×cosj2. Substituted expressionsf1 and f2 in the formula (7), we’ll find the sought-for charge:
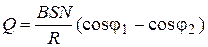 . (8)
. (8)
Let’s check if the right part of the formula gives (4) the unit of EMF (В), and the right part of the formula (8) the unit of charge (C):
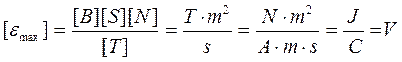 ;
;
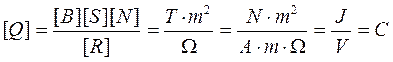 .
.
Let’s make the calculations:
 ;
;

Result: 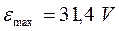 ,
, 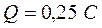 .
.
Individual tasks for PROBLEM 2.4.
