ВНИМАНИЕ! Для работы компонента MagicPlot для анализа данных необходимо установить последнюю версию исполняющей среды Java 6 (Runtime библиотеки виртуальной машины Java).

Рис. 4.3. Компонент для анализа данных, получаемых на лабораторной установке.

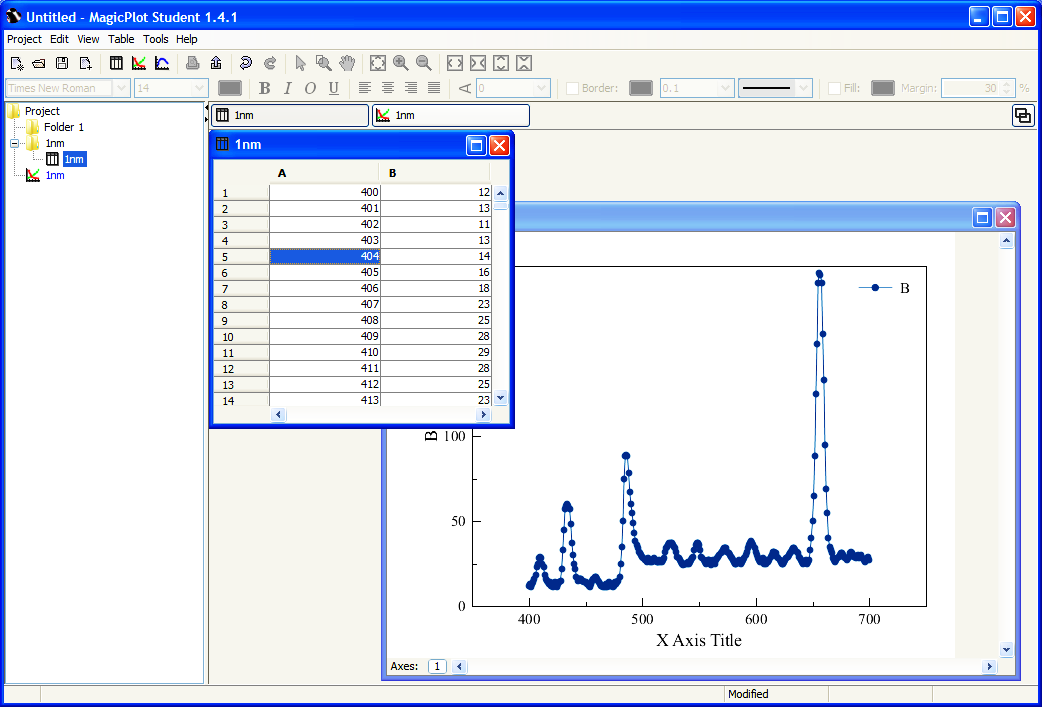Для импорта данных в подпрограмму — анализатор следует воспользоваться командой Project — Import Text Table. При этом откроется стандартное диалоговое окно выбора файла рис. 4.4.

После импорта файла данных автоматически заполнятся столбцы таблицы A, B компонента. Для построения графика следует выделить мышью столбцы А и В таблицы, для чего, удерживая клавишу Ctrl, щелкнуть левой кнопкой мыши на заголовке столбцов «А», затем «В» и использовать команду Table — Create Fit Plot – Line для отображения данных в виде плавной линии либо Table — Create Fit Plot - Marker, Line&Marker для отображения данных в виде экспериментальных точек.

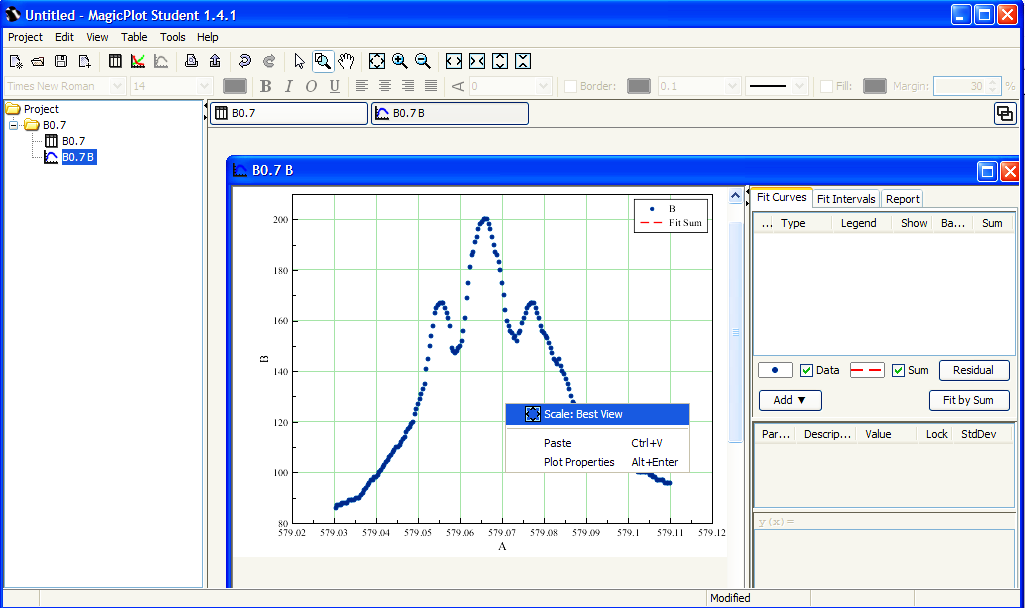
В появившемся окне графика данных щелкнуть правой кнопкой мыши в области окна и выбрать наилучший масштаб для отображения автоматически: Scale: Best View рис. 4.5.

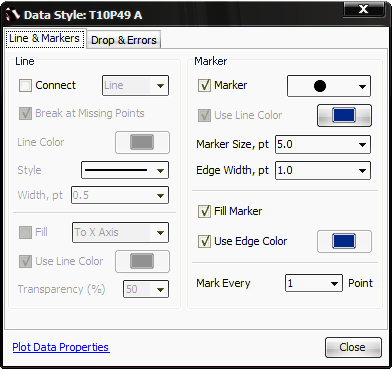
Цвет символов данных, форму символов и другие параметры можно настроить вызвав диалоговое окно Data Style рис. 4.6 двойным щелчком левой кнопкой мыши на какой-либо экспериментальной точке данных на графике.

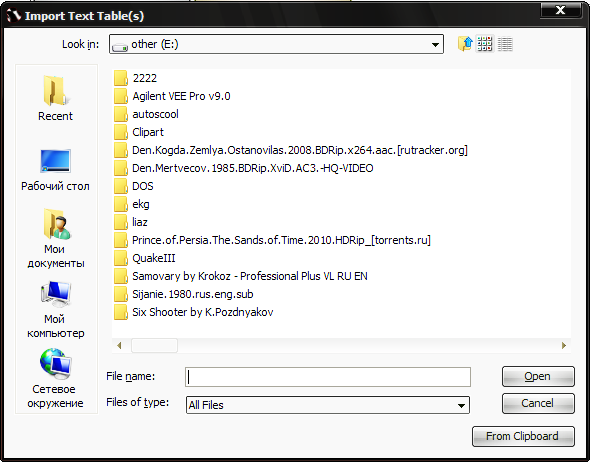
Рис. 4.4. Выбор файла для импорта данных.

Анализ данных осуществляется командой Add - с соответствующим выбором функции для анализа данных и последующим нажатием кнопки Fit One Curve для приближения экспериментальных данных единичной функцией либо Fit by Sum для фитирования данных комбинацией нескольких функций. Допускается и рекомендуется в сложных случаях проводить приближение с помощью комбинации из нескольких функций (Fit by Sum).

Рис. 4.6. Настройка изображения и стиля графика.

Рис. 4.5. Настройка автомасштаба графика.

Порядок выполнения.

1. Перед включением установки в сеть проверить целостность всех соединительных сигнальных и сетевых проводов. Все работы по подключению комплекса к компьютеру следует выполнять только при отключенных от сети приборах. Разобраться с принципиальными блок-схемами опытов, в назначении кнопок, переключателей и ручек прибора. На данном шаге НЕ подключайте прибор к USB порту ПК. Подключить осветитель к блоку управления, используя соответствующие провода из комплекта, соединив выходы «ЛАМПА» и «ФОТОДАТЧИК» с соответствующими входами осветителя. Выход «ЛАМПА» обеспечивает подачу напряжения питания на спектральную лампу, а выход «ФОТОДАТЧИК» подает соответствующие напряжения на фотодатчик.

2. При планируемой работе с ПК соединить монитор с системным блоком ПЭВМ, подключить клавиатуру и мышь к системному блоку используя стандартные провода для подключения. Подключить системный блок ПЭВМ и монитор к сети ~220 В.

3. Загрузить операционную систему согласно стандартным процедурам загрузки.

4. При необходимости, настроить компьютер для работы с учебной установкой согласно прилагаемому руководству к среде .

5. Запустить программу для работы с учебной установкой для данного эксперимента пользуясь ярлыком на рабочем столе либо другим способом, указанным лаборантом.

ПРОВЕДЕНИЕ ЭКСПЕРИМЕНТА.

6. Перед началом работы ознакомится с принципиальной схемой учебной установки, разобраться в назначении кнопок и измерительного прибора. Проверить целостность сетевого провода. Перед началом работы проверить положения всех ручек регулировки. Ручки регулировки «АНОДНЫЙ ТОК» и «ТОК НАКАЛА» для лампы ДВС-25 должны быть повернуты до упора против часовой стрелки. При этом ток накала на катод лампы не подается, анодное напряжение также выключено.

7. В начале работы следует включить источник света — лампу ДВС-25, используя переключатель «СЕТЬ. АНАЛОГОВАЯ ЧАСТЬ» и настроить лампу, соблюдая следующий порядок включения лампы ДВС-25 (при этом цифровая часть прибора должна быть отключена — измерительная система и ЖКД дисплей выключены):

a) Подать на накал (катод) лампы ток в диапазоне 2 — 2, 5 А, регулируя этот ток ручкой «ТОК НАКАЛА» и контролируя значение тока накала амперметром.

b) После примерно 30 секундного прогрева катода включается анодное напряжение плавным вращением ручки «АНОДНЫЙ ТОК». При этом должен начаться дуговой разряд в лампе.

c) Сразу после возникновения дугового разряда в лампе, снизить ток накала до значения 0,5 — 1 Ампера, регулируя этот ток ручкой «ТОК НАКАЛА» и контролируя значение тока накала амперметром.

d) Отрегулировать анодный (разрядный) ток лампы, вращением ручки регулировки «АНОДНЫЙ ТОК» и контролируя этот ток миллиамперметром. Анодный ток следует поддерживать в диапазоне 250 — 300 мА. Ток анода во время работы лампы не должен превышать 300 мА.

e) После окончательного прогрева лампы, для которого обычно требуется не более 3 — 5 минут выключить «ТОК НАКАЛА» плавно убавив его до нуля ручкой «ТОК НАКАЛА».

f) После прогрева лампы включается цифровая часть цепей питания прибора нажатием клавиши «СЕТЬ. ЦИФРОВАЯ ЧАСТЬ». Это сделано для исключения влияния паразитных переходных процессов во время включения лампы на микропроцессорную систему управления учебной установкой.

g) Для отключения установки следует сначала отключить цифровую часть кнопкой «СЕТЬ. ЦИФРОВАЯ ЧАСТЬ», при этом отключится ЖКД дисплей и измерительная система, затем ручкой регулировки «АНОДНЫЙ ТОК» убавить анодный ток лампы ДВС-25 до нуля и выключить аналоговую часть переключателем «СЕТЬ. АНАЛОГОВАЯ ЧАСТЬ».

8. После 3 — 5 минутного прогрева лампы, включается цифровая часть цепей питания прибора нажатием кнопки «СЕТЬ. ЦИФРОВАЯ ЧАСТЬ».

9. Дождаться появления системного сообщения на ЖКД LCD дисплее прибора, о дальнейшем порядке действий:

Connecting................

После появления данного сообщения на ЖКД LCD дисплее учебного прибора, можно подключить прибор к USB – порту ПК и однократно нажать кнопку «СТАРТ» в программе-оболочке (кнопка используется для конфигурации устройства сразу после включения). При этом начнется процесс инициализации прибора. При автономном режиме работы сделать это можно непосредственно с учебной установки, нажимая и удерживая кнопку «ИНИЦИАЛИЗАЦИЯ/USB» до тех пор, пока индикатор уровня инициализации на ЖКД экране не достигнет правого конца дисплея. ВНИМАНИЕ! ПОСЛЕ ИНИЦИАЛИЗАЦИИ ПРИБОРА USB ПЕРЕДАТЧИК УЧЕБНОЙ УСТАНОВКИ ОТКЛЮЧАЕТСЯ И ПРИБОР ПЕРЕХОДИТ В АВТОНОМНЫЙ РЕЖИМ РАБОТЫ. Для включения USB в приборе и последующей работы с программой приема и обработки данных, либо для отключения USB и работы в ручном режиме, следует нажимать кнопку «ИНИЦИАЛИЗАЦИЯ/USB».

10. Дать установке прогреться в течение трех минут.

11. Приступить к эксперименту по снятию спектрограммы водородной-дейтериевой лампы низкого разрешения 1 нм. Для этого с помощью кнопки «РЕЖИМ РАБОТЫ» выберите эксперимент «spectr 1 nm resol» и начните опыт.

12. Просканируйте спектр, нажимая кнопки «ДЛИНА ВОЛНЫ». При автономном режиме работы без ПК, записывайте результаты измерений в таблицу и постройте график зависимости интенсивности от длины волны I=I(λ). Спектрограмма должна иметь вид, аналогичный рис. 3.1 а). Сканирование спектра может осуществляться как по нажатию кнопок «ДЛИНА ВОЛНЫ», так и в автоматическом режиме, для этого следует перевести бегунок «АВТОСКАН» в положение «ВКЛ». Если установить флажок «ПОКАЗАТЬ ГРАФИК», то набираемая спектрограмма будет отображаться в режиме реального времени во всплывающем окне графика.

13. Сохраните результаты измерений в файл-данных на ПК.

14. Переключитесь в режим высокого разрешения 0,01 нм и повторите действия п. 12 — 13 для исследования изотопической структуры альфа-линии водородной-дейтериевой лампы. Для этого следует нажать кнопку «ЭКСПЕРИМЕНТ ПЕРЕКЛЮЧИТЬ» в программе-оболочке либо кнопку «РЕЖИМ РАБОТЫ», расположенную на передней панели лабораторного модуля. Просканируйте спектр, полученная спектрограмма должна иметь вид, аналогичный рис. 3.1 б).

15. Повторите действия по снятию спектрограмм высокого разрешения, аналогичные пп. 12 — 14 для всех линий водородно — дейтериевой лампы. Все полученные спектрограммы изотопической должны иметь вид, аналогичный рис. 3.1 б).

16. По полученной спектрограмме низкого разрешения 1 нм, определите координаты пиков (центры пиков) как длины волн излучения альфа, бета, гамма и дельта линий, соответствующие линиям серии Бальмера атомарного водорода (см. рис. 3.1 а): λ_Hα , λ_Hβ, λ_Hγ, λ_Hδ.

17. Сравнить измеренные вами значения длин волн в серии Бальмера с табличными значениями, приведенными в таблице 1.

18. Для серии Бальмера формула (16) перепишется в виде:

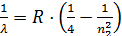(3.1)

19. С помощью формулы (3.1) вычислите для каждой линии λ_Hα , λ_Hβ, λ_Hγ, λ_Hδ постоянную Ридберга Ri. Не забудьте все вычисления производить в СИ. Вычислите и запишите среднее значение <R> .

20. Из формулы 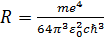получите выражение для вычисления постоянной Планка. Используя среднее значение <R>, с помощью этого выражения вычислите постоянную Планка.

При вычислении принять: m=9∙10-31 кг, e=1,6∙10-19Кл, ε0=8,85∙10-12 Ф/м, с=3∙108м/c.

21. Сравнить полученное значение постоянной Ридберга Rэкспер.с теоретическим значением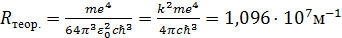

22. По полученным спектрограммам высокого разрешения для каждой линии (альфа, бета и гамма) определите координаты пиков (их центры) как длины волн, соответствующие линиям водорода Н и дейтерия D (см. рис. 3.1 б).

23. Рассчитайте экспериментальное значение величины изотопического сдвига 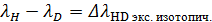в структуре каждой из линий водородной-дейтериевой лампы, спектр которой был снят вами с высоким разрешением 0,01 нм.

24. По формуле (2.27) рассчитать экспериментальное значение отношения массы электрона к массе протона 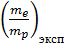по величине изотопического сдвига 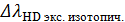, найденного для каждой линии излучения серии Бальмера из снятых вами спектрограмм высокого разрешения. По результатам расчетов определить среднее значение 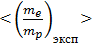и сравнить его с табличными данными. Все расчеты производите в СИ.

25. Рассчитайте по формуле (2.26) теоретическое значение изотопического смещения для каждой линии излучения серии Бальмера в спектре водородной-дейтериевой лампы. При расчетах принять: масса электрона m_e=m=9∙10-31 кг; масса ядра атома водорода (масса протона) М_H=m_p=1,67∙10-27 кг; λ_H – длина волны излучения атома водорода для данной линии.

26. Сравните полученные Вами результаты с данными таблицы 1. Объясните возможные расхождения в расчетах и сделайте выводы о точности эксперимента. При сравнении результатов учтите, что все данные в таблице 1 приведены в Ангстремах (1 Å = 0,1 нм=10^-10 м).

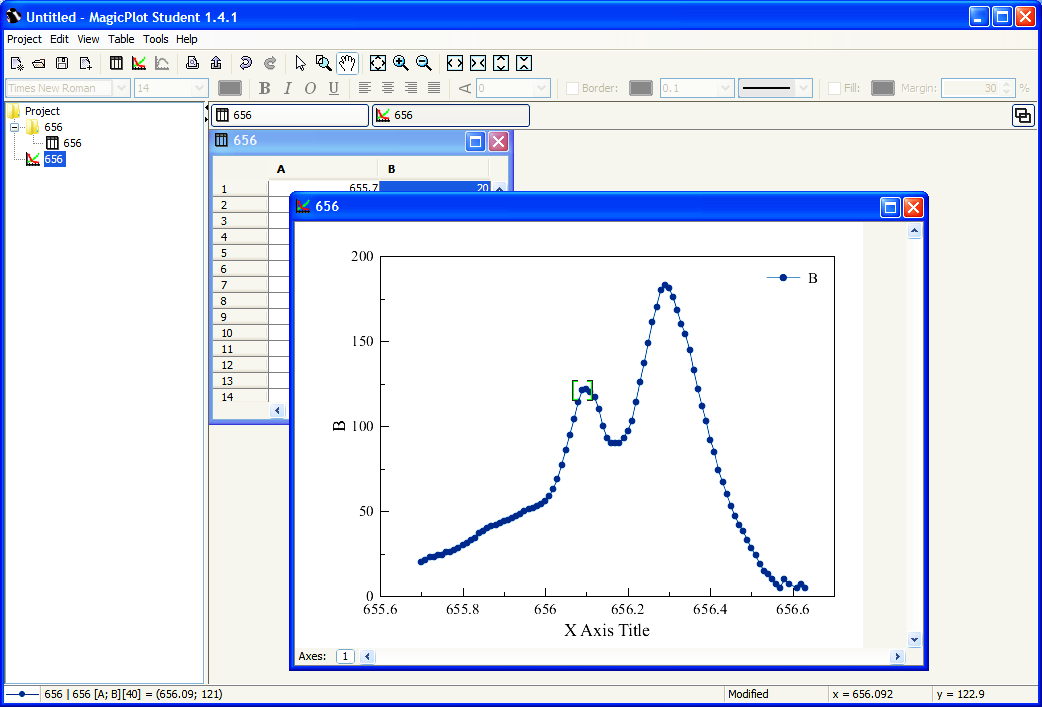
27. При работе в автоматизированной среде с компонентом анализа данных компонентом LabVisual «MagicPlot», текущее положение курсора в координатах {длина волны, интенсивность} отображается внизу слева от графика рис. 4.7 (жирное выделение), что позволяет, подведя указатель мыши к тому или иному пику, достаточно точно установить положение его центра, а затем вычислить изотопического смещение.

28.

Рис. 4.7. Определение положения центра пика. Показана изотопическая структура альфа-линии спектра испускания водородной-дейтериевой лампы.

По окончании работы следует сначала отключить цифровую часть кнопкой «СЕТЬ. ЦИФРОВАЯ ЧАСТЬ», при этом отключится ЖКД дисплей и измерительная система, затем ручкой регулировки «АНОДНЫЙ ТОК» убавить анодный ток лампы ДВС-25 до нуля и выключить аналоговую часть переключателем «СЕТЬ. АНАЛОГОВАЯ ЧАСТЬ».

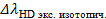КОНТРОЛЬНЫЕ ВОПРОСЫ.

1. Воспользовавшись квазиклассической теорией Бора, получить формулу для энергии электрона Еnв однократно ионизированном атоме гелия. В чём, по вашему мнению, основной недостаток теории Бора?

2. Пользуясь энергетической диаграммой для атома водорода, представленной на рисунке 1.1, определите энергию ионизации атома водорода. Определить по той же диаграмме первый потенциал возбуждения атома водорода.

3. Что такое линейчатый и сплошной спектр? Какой спектр вы наблюдали в этом опыте?

4. Почему спектр водорода и других газов линейчатый, а спектр лампы накаливания сплошной?

5. Получите обобщенную формулу Бальмера (16) и выражение Rтеоретич.через основные константы.

6. Определить энергию фотона, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на основной.

7. Во сколько раз минимальная длина волны в серии Пашена спектра водорода больше максимальной длины волны в серии Бальмера?

8. Вычислить наибольшие длины волн в сериях Лаймана, Бальмера, Пашена в спектре водорода.

9. Объясните причины размытия энергетических уровней электрона в атоме. Какой уровень будет «размыт» в наименьшей степени. Почему?

10. Какой метод возбуждения атомов для получения спектра используется в данной установке? Объясните методику эксперимента: необходимость в монохроматоре, принцип его устройства, принцип работы излучателя.

11. Как вы думаете, как меняется после включения высокого напряжения сопротивление газоразрядного промежутка в лампах ДВС-25? Чему равно сопротивление этого промежутка до включения и после? Почему происходит резкое изменение сопротивления трубки? С какими физическими явлениями, происходящем в газе, заполняющим трубку, это связано?

12. Какова физическая природа изотопического эффекта?

13. Как зависит постоянная Ридберга от массы ядра?

14. Вывести рабочую формулу для определения 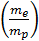из спектроскопических измерений.

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА.

1. Иродов И. Е., Квантовая физика. Основные законы., М. 2002
2. Савельев И. В. Курс общей физики. М., 1982, т. 3
3. Шпольский Э. В., Атомная физика т.1, т.2
4. Курс физики, под редакцией Лозовского В.Н., С-Пб 2001.
5. Рохлин Г. Н., Разрядные источники света, М., Энергоатомиздат,1991.
6. Лабораторный практикум по физике, под ред. К. А. Барсукова, М. 1988.
7. Давыдов А. С., Квантовая механика, Наука, 1973, издание – 2-ое.
8. П. В Елютин, Квантовая механика с задачами. Наука, 1976.
9. И. И. Гольдман. Сборник задач по квантовой механике., 1957.
10. М. И. Фугенфиров. Электрические схемы с газоразрядными лампами
11. В. М. Скобелев. Источники света и пускорегулирующая аппаратура.

Лабораторная работа № 3

ЭФФЕКТ ЗЕЕМАНА

Магнитные свойства атома

Магнетизм атома порождается тремя причинами:

· орбитальным движением электронов, создающим орбитальный механический 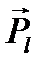и магнитный момент 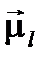каждого из них;

· спиновыми свойствами электрона – существованием у него собственных механического 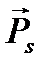и магнитного 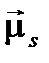моментов;

· такими же свойствами многих атомных ядер, обладающих собственными механическим 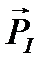и магнитным 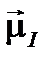моментами.

Обращение каждого электрона вокруг ядра представляет собой аналог кругового тока силой 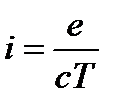, создающего орбитальный магнитный момент

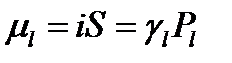, (1.1)

где S – площадь контура, обегаемого электроном;

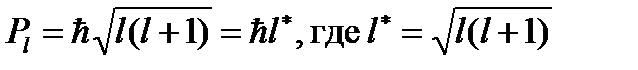
механический момент орбитального движения электрона; l – орбитальное квантовое число, а

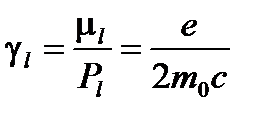(1.2)

так называемое гиромагнитное отношение орбитального движения электрона^[2].

Складываясь векторно, орбитальные магнитные моменты всех электронов атома образуют результирующий магнитный момент 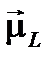всей электронной оболочки:

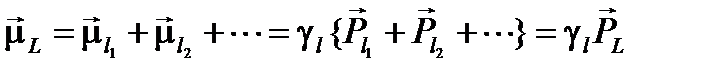(1.3)

Здесь

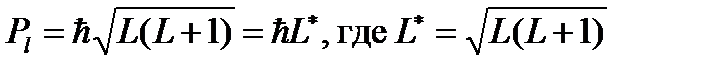
– суммарный орбитальный механический момент атом; L – орбитальное квантовое число атома.

Спиновый магнитный момент 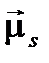электрона связан с его механическим моментом 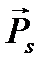соотношением

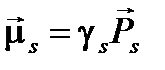, (1.4)

где

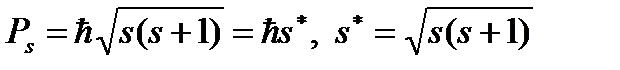
– спиновый механический момент электрона; s – спиновое квантовое число, а

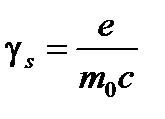(1.5)

– его спиновое гиромагнитное отношение. Оно, как видим, вдвое больше аналогичной величины для орбитального движения:

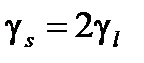. (1.6)

Это обстоятельство получило в свое время название гиромагнитной аномалии и, хотя с современной точки зрения здесь нет ничего аномального, название удержалось до сих пор.

Сумма спиновых магнитных моментов всех электронов оболочки образует результирующий спиновый магнитный момент 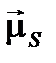атома:

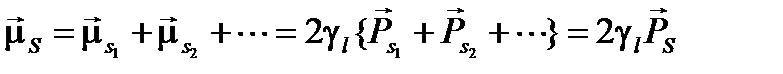(1.7)

где .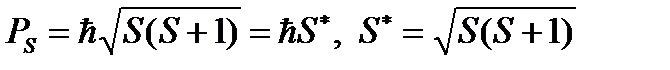

Здесь 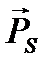– суммарный спиновый механический момент атома; S – спиновое квантовое число атома.

Если в формулах (1.1) и (1.4) заменить входящие в них величины соответствующими значениями, то получим для орбитального и спинового магнитных моментов электрона соотношения:

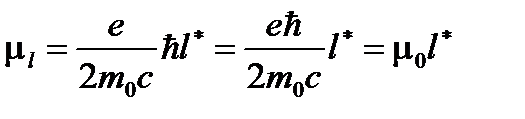, (1.8)

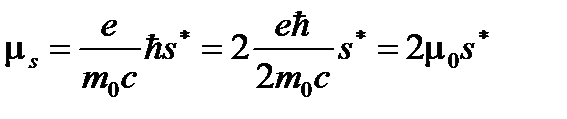. (1.9)

Величина

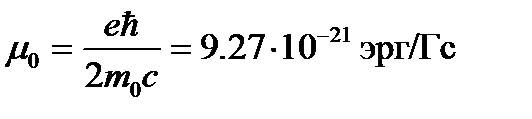(1.10)

называется магнетоном Бора и служит единицей для измерения атомных магнитных моментов.

Квантовые числа l и s принимают значения:

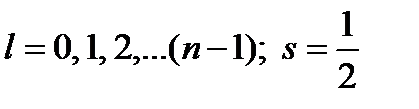(1.11)

где n = 1, 2, 3,… – главное квантовое число.

Это значит, что спиновый магнитный момент электрона приблизительно равен двум магнетонам Бора:

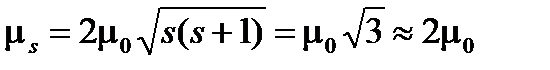, (1.12)

в то время как его орбитальный магнитный момент имеет величины разные для различных состояний электрона в атоме, причем при

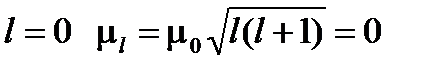
Заметим, что равенство (1.12) не имеет большого физического значения, поскольку в эксперименте проявляется не 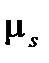, a его проекция на заданное полем направление; проекция же эта, как показывают данные, равна по абсолютной величине одному магнетону Бора 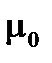(см. формулу (1.14)).

Магнитные моменты 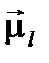и 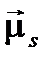ориентированы антипараллельно соответствующим механическим моментам 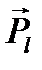и 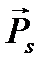, так как заряд электрона отрицателен (см. рис. 1).

Рис. 1. Механические и магнитные моменты электрона в атоме

Направления 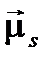и 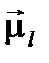. относительно друг друга (так же, как направления квантовых векторов вообще относительно заданной оси в пространстве) определяются правилами пространственного квантования: можно точно указать значение проекции квантового вектора на заданную ось, но нельзя одновременно с тем определить другие компоненты этого вектора. Проекции орбитального и спинового механических и магнитных моментов электрона на ось, заданную направлением постоянного намагничивающего поля 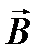, соответственно равны:

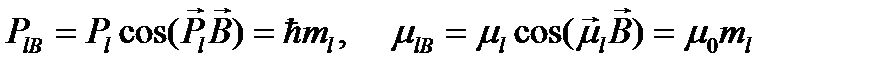, (1.13)

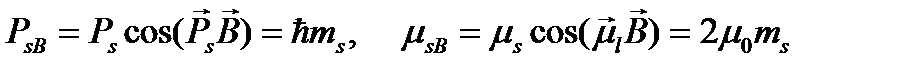, (1.14)

где 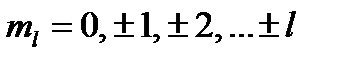– орбитальное магнитное квантовое число электрона; 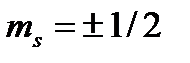– его спиновое магнитное квантовое число.

Таким образом, орбитальные механический и магнитный моменты 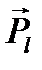и 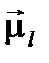могут относительно поля 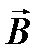принимать 2l+1 различные ориентации, а их проекци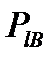и и 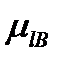имеют 2l+1 возможные значения.

Проекции вектора 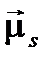направлены либо вдоль 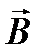, либо против него и равны 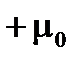и 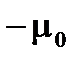соответственно.

Сумма результирующих орбитального 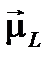и спинового 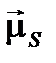магнитных моментов атома определяет его результирующий магнитный момент:

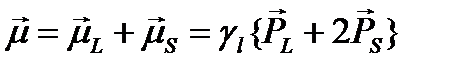. (1.15)

Поскольку полный механический момент атома 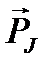равен

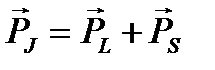, (1.16)

где

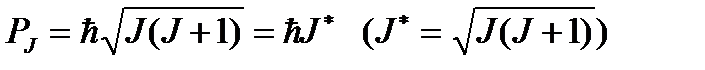, (1.17)

(J – внутреннее квантовое число атома, применяющее значения из ряда J = L+S, L+S–1, …, L–S), то из (1.15) и (1.16) следует, что вектор 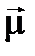составляет с вектором 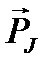угол, отличный от 180° (следствие гиромагнитной аномалии).

Схема сложения моментов 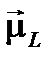и 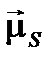в результирующий магнитный момент 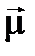всей электронной оболочки представлена на рис. 2. (в избранном на рис. 2 масштабе длина вектора 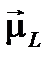равна длине вектора 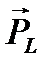; в силу гиромагнитной аномалии в этом масштабе длина вектора 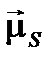, вдвое больше длины .).

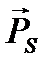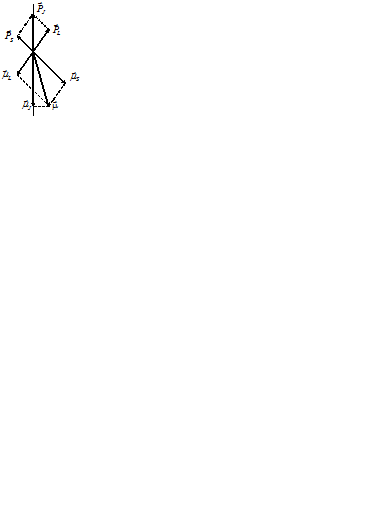
Рис. 2. Сложение механических и магнитных моментов электронной оболочки атома

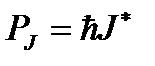
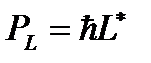
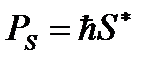
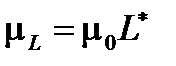
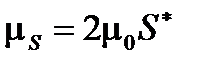
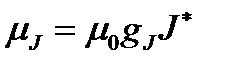
Так как вся система векторов вращается вокруг оси совпадающей с направлением вектора 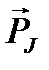, то физическое значение имеет не вектор 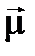, а только его слагающая 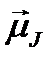. Вектор 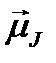называется эффективным магнитным моментом атома или просто магнитным моментом атома.

Таким образом, эффективный магнитный момент атома 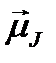антипараллелен 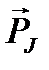и численно равен

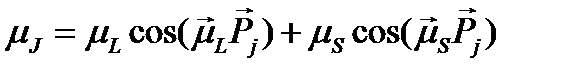. (1.18)

Несложные вычисления (см. рис. 2) дают:

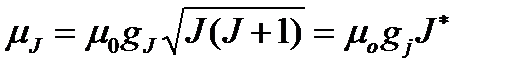, (1.19)

где

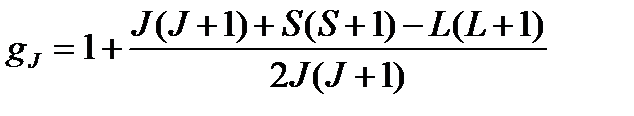(1.20)

– так называемый фактор Ланде, или фактор спектроскопического расщепления электронной оболочки атома. Из (1.20) следует, что величина фактора Ланде зависит от состояния атома. По величине этого множителя можно сделать качественные заключения о происхождении магнетизма данного атома: если 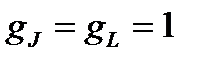, то это возможно при S = 0, но тогда m_S = 0, и магнетизм создается только за счет орбитального движения электронов. Если же 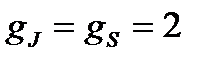(точнее 2,00238), то это возможно при m_L = 0, но тогда L = 0, и магнетизм имеет чисто спиновое происхождение. Разумеется, возможны и промежуточные случаи.

В случае же конденсированных веществ, когда взаимодействие данного атома с атомами вещества может быть значительным, g-фактор по своей величине может отличаться от того, что дает формула (1.20). Эти различия дают возможность судить как о характере взаимодействия атомов, таи и о природе магнетизма данного вещества.