Метод кодирования Шеннона-Фано

При кодировании по методу Шеннона следует придерживаться следующих правил.

1. Все сообщения ансамбля ранжируются в порядке убывания вероятности реализаций сообщений.

2. Сообщения делятся на две группы сообщений, приблизительно одинаковые по вероятности.

3. Всем сообщениям одной из подгрупп приписывается символ 1, другой – символ 0.

4. Сообщения каждой подгруппы опять делятся на две подгруппы, приблизительно одинаковые по вероятности, и приписываются символы 1и 0.

5. Процедура деления и приписывания символов 1 и 0 продолжается до тех пор пока не останется в каждой подгруппе по одному сообщению.

6. Полученная последовательность символов, соответствующая определённому сообщению, является отображением сообщения в двоичной системе счисления в сжатой форме.

Ввиду того, что производится последовательная процедура деления множества символов на подгруппы, количество символов в коде, соответствующее определённому сообщению, будет зависеть от вероятности реализации сообщения. В этом случае метод кодирования характеризуется средним числом символов

,

где - количество символов, употребляемых для кодирования -го сообщения.

Пример 3.2. Процедура кодирования изложена в таблице 3.3.

Таблица 3.3
Анс-ль	Вер. P						Коды	Условн. вер.
	0.20
	0.2							2/3
	0.19							1/3
	0.15							2/3
	0.10							1/3
	0.08							1/3
	0.06							1/4
	0.01							1/5
	0.01

В примере используется тот же ансамбль сообщений с теми же вероятностями реализаций элементов ансамбля. В колонке 3 показано разбиения множества сообщений на

два подмножества и . Далее в колонках 4 – 7 показана процедура разбиения каждого подмножества до получения подмножества, состоящего из одного сообщения. Коды, соответствующие каждому сообщению, отображены жирными символами. Все полученные коды сведены в восьмую колонку.

Кодовое дерево для рассматриваемого примера приведено на рисунке 1.2.

Как видно из таблицы и рисунка 1.2, из узлов, отображающие коды, не выходит ни одна ветвь, т.е. получен префиксный код. На кодовом дереве из узла с кодом 100 выходят ветви и останавливаются на уровне пятиразрядного кода. При этом число неиспользуемых кодов равно 4.

Характеристик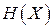и , , , , остаются неизменными

3.16993 .

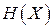=2.79465

0.881615 , 0.118385.

1 .

Рассмотрим ансамбль . По формуле полной вероятности получим = 0.57367, = 0.42633.

Количество информации, содержащееся в каждом символе ансамбля Y равно соответственно

0.801707 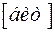, 1.22996 .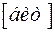

Энтропия ансамбля Y равна

0.984283 .

Соответственно коэффициент сжатия и коэффициент избыточности будут равны

0.984283, 0.015717

Сравнивая коэффициенты сжатия и коэффициенты избыточности ансамблей X и Y видно при кодировании по методу Шеннона, произошло увеличение коэффициента сжатия и уменьшение избыточности ансамбля Y. Относительные величины равны соответственно

= 1.11645 , = 7.53229.

=

=2*0.2+3*(0.2+0.19+0.15+0.1+0.08)+4*0.06+5*(0.01+0.01)= 2.9

Метод кодирования Хафмана

Правило образования кодов состоит из следующих пунктов.

1. Все сообщения ансамбля ранжируются в порядке убывания вероятности реализаций сообщений.

2. Последние два сообщения объединяются в одно сообщение с вероятностью реализации, равной сумме вероятностей, объединяемых сообщений.

3. Полученные сообщения вновь ранжируются в порядке убывания вероятности реализаций сообщений.

4. Процедура объединения и ранжирования сообщений продолжается до тех пор, пока не останется одно сообщение с вероятностью реализации, равной 1.

5. В результате процедуры объединения и ранжирования сообщений получается кодовое дерево. Каждому лучу, исходящему из узла, в котором объединяются сообщения, приписываются символы 1 и 0, ( скажем, верхнему лучу приписывается символ 1, нижнему – символ 0).

6. Запись кода, соответствующего -му сообщению можно начинать как с вершины кодового дерева, так и с ветви , соответствующего -му сообщению. Если записывать код сообщения с ветви, соответствующего -му сообщению, получается не префиксный код. Поэтому рекомендуется производить считывание кода, начиная с вершины кодового дерева к ветви, содержащей -ое сообщение.

Процедура кодирования демонстрируется на примере.

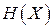Пример 3. В примере используется тот же ансамбль сообщений с теми же вероятностями реализаций элементов ансамбля. Характеристики , , , , остаются неизменными. На рисунке 1.3 показана реализация правила кодирования сообщений. В результате считывания символов, начиная с ветви -го сообщения, получены не префиксные коды. Для получения префиксных кодов производится зеркальное отображение не префиксных кодов, что показано в таблице 1

Характеристик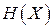и , , , , остаются неизменными.

Рассмотрим ансамбль . По формуле полной вероятности получим = 0.5303, = 0.4697.

Количество информации, содержащееся в каждом символе ансамбля Y равно соответственно

0.91511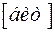9 , 1.09019 .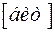

Энтропия ансамбля Y равна

0.997349 .

Соответственно коэффициент сжатия и коэффициент избыточности будут равны

0.997349, 0.00265

Таблица 3.4
X	Вер.	не префиксный код	префиксный код		Условн. вер.
	0.2
	0.2				1/2
	0.19				1/3
	0.15				2/3
	0.10				1/3
	0.08				1/4
	0.06				1/5
	0.01				1/6
	0.01

На рисунке 3.5 приведено кодовое дерево, полученное при кодировании по методу Хафмена ансамбля X.

Сравнивая коэффициенты сжатия и коэффициенты избыточности ансамблей X и Y видно при кодировании по методу Хафмана, произошло увеличение коэффициента сжатия и уменьшение избыточности ансамбля Y по сравнению с равномерным кодом.

Средняя длина кода при кодировании по методу Хафмана уменьшилась также и равна

=1.34 .

Как видно из рисунка 3.5, ни одна кодовая комбинация не является началом другой кодовой комбинации, т.е. код является префиксным. Свойство префиксности кода позволяет однозначно декодировать последовательность кодовых комбинаций, что видно из таблицы 3.4 и рисунка 3.5.

Следует отметить, метод кодирования Хафмана позволяет получить показатели , , , более высокие, чем при кодировании по методу Шеннона. Это объясняется тем, что в методе кодирования по Шеннону допускается некоторый произвол при делении множества событий на группы.