Приклади характерних задач з розв’язанням. Задача 1. Ідеальний газ знаходиться в адіабатно ізольованому об’ємі під постійним зовнішнім тиском Р0

Задача 1. Ідеальний газ знаходиться в адіабатно ізольованому об’ємі під постійним зовнішнім тиском Р₀ . Безпосереднім розрахунком варіацій ентропії 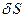, показати, що при рівновазі ентропія такої системи виявляється максимальною.

Розв’язання. З основного рівняння термодинаміки для PV-систем (3.13) у разі ідеального газу можна записати

, (1)

де - кількість молів газу.

У нашому випадку з першого начала маємо

,

що дозволяє зобразити (1) у вигляді

, (2)

де тиск газу. Отже, бачимо, що рівновага можлива лише при . Покажемо також, що в цьому разі ентропія максимальна.

Інтегруючи (1) при зміні температури від 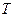до , а об’єму від 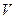до , одержимо

. (3)

Розкладуючи (3) за степенями і , матимемо

де

.

Оскільки значення виявляється від’ємним при будь-яких і , ентропія цієї системи в стані рівноваги максимальна.

Задача 2. Як наслідок електронної емісії у порожнині всередині металу виникає електронний газ. Виходячи з мінімуму вільної енергії при рівновазі визначити густину електронного газу в цій порожнині, як функцію температури . Вважати, що ентропія електронного газу дорівнює ентропії одноатомного ідеального газу.

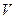Розв’язання. При тепловій рівновазі кількість електронів, що випускається за одиницю часу, дорівнює їх кількості, що поглинається. Рівноважна густина електронів визначається з загальної умови рівноваги , яка при сталих і 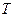дає конкретну умову

~ . (1)

Розрахуємо вільну енергію 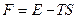газу електронів. Внутрішня енергія 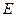цього газу складається з середньої кінетичної енергії та суми робіт виходу електрона з металу:

. (2)

Ентропію беремо за формулою (3.27):

, (3)

де - ентропійна стала, яка розрахована методами статистичної фізики. Отже, маючи на увазі, що , , запишемо вільну енергію 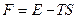у вигляді

. (4)

З умови (1) остаточно знаходимо рівноважну густину електронного газу в порожнині

, (5)

де .

За допомогою (5) можна безпосередньо визначати силу струму насичення розжареного катода.

Задача 3. Показати, що відповідну до детермінанта стійкості 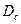матрицю можна звести до діагональної форми.

Розв’язання. Детермінант (8.16), враховуючи властивості якобіанів, можна записати як

,

що й вказує на діагональний вигляд відповідної матриці.

Задача 4. Довести вираз принципу Ле Шателье-Брауна (8.18) безпосереднім розрахуванням на прикладі ідеального газу.

Розв’язання. Оскільки завжди , нерівність (8.18) можна записати у вигляді

(1)

або через якобіани:

. (2)

Ліву частину (2), користуючись властивістю якобіанів, перепишемо як

. (3)

Беручи до уваги результат задачі 1 розділу 3, праву частину (3) можна зобразити через відношення теплоємностей, тобто

.

Оскільки для ідеального газу завжди нерівність (8.18) можна вважати доведеною.