Глава 1 математические модели сигналов 4 страница

Среди случайных процессов с дискретным множеством состояний нас будут интересовать такие, у которых статистические зависимости распространяются на ограниченное число k следующих друг за другом значений. Они называются обобщенными марковскими процессами k-го порядка.

Вероятностные характеристики случайного процесса. В соответствии с определением случайный процесс U(t) может быть описан системой N обычно зависимых случайных величин U₁ = U(t₁), ..., U_i= U(t_i), ..., U_N = U(t_N), взятых в различные моменты времени t₁...t_i...t_N. При неограниченном увеличении числа N такая система эквивалентна рассматриваемому случайному процессу U(t).

Исчерпывающей характеристикой указанной системы является N-мерная плотность вероятности p_N(U₁, ..., U_i, ..., U_N; t₁, ..., t_N). Она позволяет вычислить вероятность Р_N реализации, значения которой в моменты времени t₁,t₂, ...,t_N будут находиться соответственно в интервалах (u₁, u₁+Δu₁), ..., (u_i, u_i+ u_i), ..., (u_N, u_N + u_N), где u_i(1 ) —значение, принимаемое случайной величиной U_i, (рис. 1.12).

Если Δu_i, выбраны достаточно малыми, то справедливо соотношение

Получение N-мерной плотности вероятности на основе эксперимента предполагает статистическую обработку реализаций, полученных одновременно от большого числа идентичных источников данного случайного процесса. При больших N это является чрезвычайно трудоемким и дорогостоящим делом, а последующее использование результатов наталкивается на существенные математические трудности.

На практике в таком подробном описании нет необходимости. Обычно ограничиваются одно- или двумерной плотностью вероятности.

Одномерная плотность вероятности p₁(U₁; t₁) случайного процесса U(t) характеризует распределение одной случайной величины U₁, взятой в произвольный момент времени t₁. В ней не находит отражения зависимость случайных величин в различные моменты времени.

Двумерная плотность вероятности p₂ = p₂(U₁, U₂; t₁, t₂) позволяет определить вероятность совместной реализации любых двух значений случайных величин U₁ и U₂ в произвольные моменты времени t₁ и t₂ и, следовательно, оценить динамику развития процесса. Одномерную плотность вероятности случайного процесса U(t) можно получить из двумерной плотности, воспользовавшись соотношением

Использование плотности вероятности даже низших порядков в практических приложениях часто приводит к неоправданным усложнениям. В большинстве случаев оказывается достаточно знания простейших характеристик случайного процесса, аналогичных числовым характеристикам случайных величин. Наиболее распространенными из них являются моментные функции первых двух порядков: математическое ожидание и дисперсия, а также корреляционная функция.

Математическим ожиданием случайного процесса U(t) называют неслучайную функцию времени m_u(t₁), которая при любом аргументе t₁ равна среднему значению случайной величины U(t\) по всему множеству возможных реализаций:

Степень разброса случайных значений процесса U(t₁) от своего среднего значения m_u(t₁) для каждого t₁ характеризуется дисперсией Du(t₁):

где (t₁) = U(t₁) — m_u(t₁) — центрированная случайная величина.

Дисперсия Du(t₁) в каждый момент времени t₁ равна квадрату среднеквадратического отклонения s_u(t₁):

Случайные процессы могут иметь одинаковые математические ожидания и дисперсии (рис. 1.13, а, б), однако резко различаться по быстроте изменений своих значений во времени.

Для оценки степени статистической зависимости мгновенных значений процесса U(t) в произвольные моменты времени t₁ и t₂ используется неслучайная функция аргументов R_u(t_1,t₂), называемая автокорреляционной или просто корреляционной функцией.

При конкретных аргументах t₁ и t₂ она равна корреляционному моменту значений процесса U(t₁) и U(t₂):

Через двумерную плотность вероятности выражение (1.71) представляется в виде

В силу симметричности этой формулы относительно аргументов справедливо равенство

Для сравнения различных случайных процессов вместо корреляционной функции удобно пользоваться нормированной функцией автокорреляции:

Из сравнения (1.69) и (1.70) следует, что при произвольном t₁ = t₂ автокорреляционная функция вырождается в дисперсию:

а нормированная функция автокорреляции равна единице:

Следовательно, дисперсию случайного процесса можно рассматривать как частное значение автокорреляционной функции.

Аналогично устанавливается мера связи между двумя случайными процессами U(t) и V(t). Она называется функцией взаимной корреляции:

§ 1.9. СТАЦИОНАРНЫЕ И ЭРГОДИЧЕСКИЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ

Случайные процессы различаются по степени однородности протекания их во времени. В общем случае процесс может иметь определенную тенденцию развития и характеристики, зависящие от начала отсчета времени. Такие случайные процессы называются нестационарными.

Для описания сигнала математическая модель в виде нестационарного случайного процесса подходит наилучшим образом, но неконструктивна в силу своей чрезмерной сложности.

Поэтому очень часто вводят предположение о стационарности случайного процесса, что позволяет существенно упростить математический аппарат исследования.

Случайный процесс называют стационарным в узком смысле, если выражения для плотностей вероятности не зависят от начала отсчета времени, т. е. справедливо соотношение

где U —случайная величина, отражающая значение процесса в момент времени t = t_i + τ (τ — произвольное число).

Иначе говоря, стационарность процесса предполагает его существование и статистическую однородность во всем диапазоне времени от - до + .

Такое предположение противоречит физическим свойствам реальных сигналов, в частности тому, что всякий реальный сигнал существует лишь в течение конечного отрезка времени. Однако аналогично установившимся детерминированным процессам случайные процессы, протекающие в установившемся режиме системы при неизменных внешних условиях на определенных отрезках времени, с известным приближением можно рассматривать как стационарные.

При решении многих технических задач идут на дальнейшее упрощение модели, рассматривая случайный процесс стационарным в широком смысле. Процесс U(t) принято называть стационарным в широком смысле, если выполняется условие постоянства математического ожидания и дисперсии, а корреляционная функция не зависит от начала отсчета времени и является функцией только одного аргумента τ = t₂ - t₁, т.е.

Так как условие постоянства дисперсии является частным случаем требования к корреляционной функции при τ = 0:

то выполнения соотношений (1.79) и (1.81) достаточно, чтобы рассматривать случайный процесс U(t) как стационарный.

Всякий стационарный случайный процесс является стационарным в широком смысле. В дальнейшем, если это не оговорено особо, стационарность будем рассматривать в широком смысле.

Случайные процессы, наблюдаемые в устойчиво работающих реальных системах, имеют конечное время корреляции. Поэтому для стационарных процессов, представляющих практический интерес, справедливо соотношение

Если для случайного процесса равенства (1.79), (1.81) не выдерживаются, но на интересующем нас интервале времени изменением указанных параметров можно пренебречь, его называют квазистационарным.

Среди стационарных случайных процессов многие удовлетворяют свойству эргодичности. Оно проявляется в том, что каждая реализация случайного процесса достаточной продолжительности несет практически полную информацию о свойствах всего ансамбля реализаций, что позволяет существенно упростить процедуру определения статистических характеристик, заменяя усреднение значений по ансамблю реализаций усреднением значений одной реализации за длительный интервал времени.

Следовательно, для стационарных эргодических процессов справедливы соотношения

где u(t) — конкретная реализация случайного процесса U(t).

Результаты исследования случайных процессов в их временном представлении, т. е. с использованием формул (1.83) и (1.85), лежат в основе корреляционной теории сигналов.

Для облегчения практического определения корреляционных функций в соответствии с (1.85) серийно выпускаются специальные вычислительные устройства — коррелометры (корреляторы).

§ 1.10. СПЕКТРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ СЛУЧАЙНЫХ СИГНАЛОВ

В § 1.2 была показана эффективность представления детерминированных сигналов совокупностью элементарных базисных сигналов для облегчения анализа прохождения их через линейные системы. Аналогичный подход может быть использован и в случае сигналов, описываемых случайными процессами [21].

Рассмотрим случайный процесс U(t), имеющий математическое ожидание m_u(t). Соответствующий центрированный случайный процесс (t) характеризуется в любой момент времени t₁ центрированной случайной величиной (t₁):

Центрированный случайный процесс (t) можно, как и ранее [см. (1.1)], выразить в виде конечной или бесконечной суммы ортогональных составляющих, каждая из которых представляет собой неслучайную базисную функцию j_k(t) с коэффициентом C_k, являющимся случайной величиной. В результате имеем разложение центрированного случайного процесса (t):

Случайные величины С_k называются коэффициентами разложения. В общем случае они статистически зависимы, и эта связь задается матрицей коэффициентов корреляции . Математические ожидания коэффициентов разложения равны нулю. Неслучайные базисные функции принято называть координатными функциями.

Для конкретной реализации коэффициенты разложения являются действительными величинами и определяются по формуле (1.7).

Предположив, что

детерминированную функцию mu(f) в (1.86) на интервале —T<t<.T также можно разложить по функциям φ_k(t), представив в виде

Подставляя (1.87 а) и (1.876) в (1.86) для случайного процесса U(t) с отличным от нуля средним, получим

Выражение случайного процесса в виде (1.87 в) позволяет существенно упростить его линейные преобразования, поскольку они сводятся к преобразованиям

детерминированных функций [m_u(t), j_k(t)], а коэффициенты разложения, являющиеся случайными величинами, остаются неизменными.

Чтобы определить требования к координатным функциям, рассмотрим корреляционную функцию процесса (t), заданную разложением

Так как

то

Соотношение (1.88) становится значительно проще, если коэффициенты {C_k} некоррелированы (R_kl = 0 при k 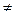l, R_kl = 1 при k = l):

В частности, при t₁ = t₂ = t получим дисперсию случайного процесса U(t):

Поэтому целесообразно выбирать такие координатные функции, которые обеспечивают некоррелированность случайных величин {С_k}. Разложение (1.87), удовлетворяющее этому условию, называют каноническим разложением.

Доказано [21], что по известному каноническому разложению корреляционной функции случайного процесса можно записать каноническое разложение самого случайного процесса с теми же координатными функциями, причем дисперсии коэффициентов этого разложения будут равны дисперсиям коэффициентов разложения корреляционной функции.

Таким образом, при выбранном наборе координатных функций центрированный случайный процесс характеризуется совокупностью дисперсий коэффициентов разложения, которую можно рассматривать как обобщенный спектр случайного процесса.

В каноническом разложении (1.87) этот спектр является дискретным (линейчатым) и может содержать как конечное, так и бесконечное число членов (линий).

Однако используются и интегральные канонические разложения в форме (1.2). В этом случае мы имеем непрерывный спектр, представляемый спектральной плотностью дисперсии.

Основным препятствием к широкому практическому использованию канонических разложений случайных процессов является сложность процедуры нахождения координатных функций. Однако для ряда стационарных случайных процессов эта процедура вполне приемлема.

§ 1.11. ЧАСТОТНОЕ ПРЕДСТАВЛЕНИЕ СТАЦИОНАРНЫХ

СЛУЧАЙНЫХ СИГНАЛОВ

Дискретные спектры. Корреляционную функцию R_u(t) (рис. 1.14) стационарного случайного процесса, заданного на конечном интервале времени [-Т, Т], можно разложить в ряд Фурье (1.15), условно считая ее периодически продолжающейся с периодом 4T (при —T<.t₁, t₂<T, -2Τ<τ<2Τ):

где

Учитывая, что R_u(t) является четной функцией, имеем

Положив τ = t₁ - t₂, находим

что согласно (1.89) представляет собой каноническое разложение корреляционной функции. По нему, как было указано ранее, получаем каноническое разложение случайного процесса:

причем

Выражение (1.95) записано для случайного процесса с нулевой постоянной составляющей, что характерно для многих реальных сигналов. В общем случае в правую часть этого выражения необходимо добавить постоянную величину, соответствующую математическому ожиданию случайного процесса (m_u). Корреляционная функция при этом не изменяется.

Очевидно, что при попарном объединении экспоненциальных составляющих с одинаковыми положительными и отрицательными индексами k каноническое разложение (1.95) приводится к тригонометрической форме.

Таким образом, стационарный случайный процесс на ограниченном интервале времени можно представить совокупностью гармонических составляющих различных частот с амплитудами, являющимися некоррелированными случайными величинами, математические ожидания которых равны нулю:

где

На спектральной диаграмме такого процесса каждой гармонике ставится в соответствие вертикальный отрезок, длина которого пропорциональна дисперсии ее амплитуды, а расположение на оси абсцисс отвечает частоте (рис. 1.15).

Чтобы получить описание стационарного случайного процесса в точном смысле, т. е. справедливое для любого момента времени на бесконечном интервале - <t< , необходимо перейти к интегральному каноническому разложению.

Непрерывные спектры. Интегральное каноническое разложение для корреляционной функции получим из формулы (1.91) путем предельного перехода при Т . Увеличение интервала времени, на котором наблюдается случайный процесс, сопровождается уменьшением значений дисперсий, что следует из (1.92), а также сокращением расстояния между спектральными линиями, поскольку

При достаточно большом, но конечном Т можно записать выражение для средней плотности распределения дисперсии по частоте:

S (w_k) = D_k/(Δω) = 2D_kT/ (k = 0,±l, ±2, ..) (1.98)

где S (w_k) - средняя плотность дисперсии на участке, прилегающем к частоте ω_k.

Теперь можно преобразовать формулы (1.94) и (1.98) к виду

Переходя к пределу при Т , получаем

где

Так как величина S (ω_k)Δω являлась не только дисперсией D_k коэффициента разложения корреляционной функции R_u(t), но и дисперсией D[C_k] коэффициента разложения случайного процесса U(t), то величина S_uu(w)dw, полученная в результате предельного перехода при Т , представляет собой дисперсию, приходящуюся на спектральные составляющие стационарного случайного процесса, занимающие бесконечно малый интервал частот (ω, ω + dw). Функцию S_uu(w), характеризующую распределение дисперсии случайного процесса по частотам, называют спектральной плотностью стационарного случайного процесса U(t).

Выражение для интегрального канонического разложения корреляционной функции R_u(t) найдем, положив в формуле (1.101) τ = t₁ - t₂:

Обозначив G (w) = С_k/( w) и повторив процедуру предельного перехода при T для соотношения (1.95), получим каноническое разложение стационарной случайной функции U(t):

где дисперсией случайной функции G(w)dw является функция S_uu(w)dw.

Поскольку понятие спектральной плотности стационарного случайного процесса играет большую роль при исследовании преобразования сигналов линейными системами, уточним ее свойства и физический смысл.

Основные свойства спектральной плотности. Отметим, что в формулах (1.101) и (1.102) S_uu(w) определена как для положительных, так и для отрицательных частот. Перейдем к одностороннему спектру, ограничиваясь только положительными частотами. Воспользовавшись формулой Эйлера, представим соотношение (1.102) состоящим из двух слагаемых:

В силу четности функции R_u(t) второе слагаемое равно нулю, а первое можно преобразовать к виду

Из (1.105) следует, что S_uu(w) является действительной и четной функцией, т. е.

Это позволяет ограничиться положительными частотами и в (1.101):

Соотношения (1 101) и (1.102), а также (1.105) и (1.107) являются парами интегрального преобразования Фурье, причем (1.105) и (1.107) для случая четной функции. Поэтому корреляционная функция и спектральная плотность подчинены закономерности: чем протяженнее кривая S_uu(ω), тем уже корреляционная функция R_u(t) (тем меньше время корреляции), и наоборот.

Площадь, ограниченная непрерывной кривой S_uu(w) на спектральной диаграмме, очевидно, должна равняться дисперсии D_u случайного процесса U(t). Действительно, положив в формуле (1.107) τ = 0, получим

Подразумевая под случайным процессом U(t) напряжение, D_u можно рассматривать как среднюю мощность, выделяемую этим напряжением на резисторе с сопротивлением в 1 Ом:

Следовательно, величина

представляет собой долю средней мощности, выделяемой составляющими спектра, относящимися к интервалу частот (ω, ω + dw).

В связи с этим спектральную плотность S_uu(w) называют еще спектральной плотностью мощности, а также энергетическим спектром стационарного случайного процесса, поскольку S_uu(w) имеет размерность энергии.

Спектральная плотность мощности случайного процесса является средней характеристикой множества реализаций. Ее можно получить и путем усреднения спектральной мощности реализации Ρ_k(ω) (1.62) по множеству реализаций.

Рассмотрим с этой целью одну реализацию u (t) стационарного случайного процесса U(t) сначала на ограниченном интервале времени -T<t<.T. Для нее можно записать преобразование Фурье:

В соответствии с (1.63) спектральная плотность мощности этой реализации

Найдем среднее значение Ρ (ω) по множеству реализации k. Имеем

или

Так как мы предполагаем, что случайный процесс U(t) стационарный, то

где t₁ - t₂ = τ.

При выполнении условия (1.114) для выражения (1.113) существует предел при T :

что и требовалось показать.

Пример 1.7. У центрированного стационарного случайного процесса спектральная плотность постоянна. Рассмотреть особенности такого процесса.

Пусть спектральная плотность S_uu(ω) ограничена определенной полосой частот (рис. 1.16, а):

В соответствии с (1.107) найдем автокорреляционную функцию процесса U(t):

Вид функции R_u(t) приведен на рис. 1.16,6. Значение ее при τ = 0 равно дисперсии, а следовательно, средней мощности рассматриваемого процесса:

Будем теперь расширять полосу частот, занимаемую энергетическим спектром (рис. 1.17, а). Интервал времени, на котором наблюдается существенная корреляционная связь значений процесса, при этом уменьшается, а дисперсия D_u возрастает.

При w₀ дисперсия становится безграничной, а корреляционная функция принимает вид дельта-функции (рис. 1.17,6).

Идеализированный случайный процесс, энергетический спектр которого безграничен и равномерен, известен как «белый шум». Такое название возникло по аналогии с белым светом, имеющим равномерный и неограниченный спектр интенсивности. Основная особенность процесса в том, что его значения в любые два сколь угодно близкие моменты времени некоррелированы. Создать белый шум принципиально невозможно, так как реальные источники сигналов всегда имеют ограниченную мощность. Тем не менее, понятие «белый шум» нашло широкое применение в информационной технике. Такая модель может быть принята, например, для сигналов (шумов), имеющих равномерный энергетический спектр в пределах полосы пропускания входного блока системы, в которой они рассматриваются.