Де - кінцева швидкість тіла.

ЗМІСТ

Прискорення____________________________ стор.2

Швидкість______________________________ стор.5

Переміщення та координати______________ стор.6

Вільне падіння__________________________ стор.9

Список використаних джерел_____________ стор.11

РІВНОПРИСКОРЕНИЙ РУХ

Рух тіла, під час якого серед інтервалів часу є такі рівні інтервали,

за які тіло здійснює неоднакові переміщення, називають

нерівномірним рухом.

Нерівномірно рухаються автомобілі, літаки та інші транспортні засоби. Нерівномірно рухаються тіла, що падають; кинуті вгору та під кутом до го­ризонту. Розглянемо такий нерівномірний рух, під час якого швидкість руху тіла за кожний однаковий інтервал часу збільшується або зменшується на певну сталу величину. Такий рух назива­ють рівноприскореним.

Рівноприскореним прямолінійним рухом тіла називають такий рух, при якому його швидкість за будь-які однакові інтервали часу змінюється на однакові величини.

Якщо у деякий початковий момент часу швидкість тіла дрівнювала v₀, а через інтервал часу t вона дорівнюватиме v, то для визначення зміни швид­кості за одиницю часу треба знайти відношення зміни швидкості до інтервалу часу,тобто прискорення.

Прискорення тіла при рівноприскореному русі характеризує бистроту зміни швидкості та визначається методом непрямих вимірювань.

Прискорення рівноприскореного прямолінійного руху — це величина, що дорівнює відношенню зміни швидкості тіла до інтервалу часу, протягом якого ця зміна відбулася:

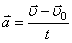
де - кінцева швидкість тіла.

Одиниця прискорення — метр у секунду за секунду (1 м/с²):

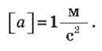
1 м/с² дорівнює прискоренню такого рівноприскореного руху тіла, при якому за 1 с швидкість тіла змінюється на 1 м/с.

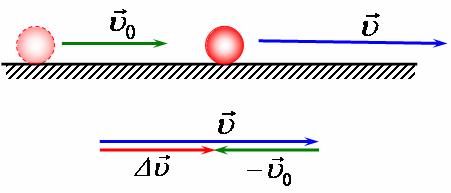
У випадку рівноприскореного руху, коли початкова швидкість менша за кінцеву, прискорення є додатною величиною (мал. 1, а),

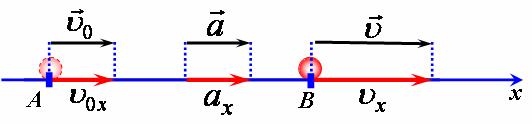
мал. 1, а

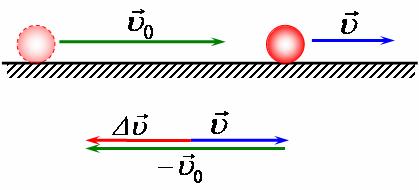
а у випадку рівноприскореного, коли початкова швидкість більпіа за кінцеву, прискорення є від'ємною величиною (рис. 1, б).

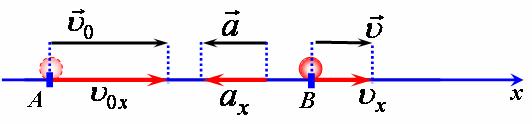
мал. 1, б

Вектор а напрямлений так само, як вектор зміни швидкості v-v₀, тобто для рівноприскореного прямолінійного руху вектор прискорення паралельний прямій траєкторії. З визначення рівноп­рискореного прямолінійного руху випливає, що його прискорення є ста­лою величиною: а = соnst.

Рівноприскорений рух може бути прискореним або сповільненим, за­лежно від швидкості руху тіла, яка відповідно збільшується або змен­шується з часом. При визначенні значення прискорення руху треба враховувати векторні властивості цієї фізичної величини. Розглянемо при­скорення та швидкість рівноприскореного руху в проекціях на вісь Ох тоді формула прискорення у проекціях матиме вигляд

Якщо швидкість руху тіла збільшується, модуль прискорення а_х>0, а його вектор збігається з напрямом руху, то рух називають рівноприскореним.

-

Якщо швидкість руху тіла зменшується, модуль прискорення а_х< 0

а його вектор буде проти­лежним напряму руху, то у цьому разі рух називатиметься рівносповільненим .

Графік проекції прискорення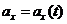

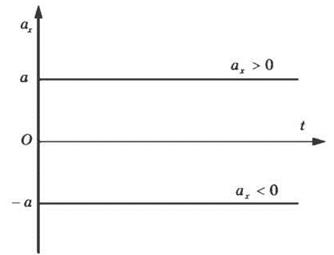
Залежність проекції прискорення від часу — пряма, паралельна осі часу t. Якщо проекція додатна, то пряма розміщується над віссю, якщо від'ємна — під нею.

Швидкість

З’ясуємо, як під час рівноприскореного рівномірного руху тіла змінюється його швидкість і як визначається пройдений ним шлях.

Із формул для прискорення легко отримати кінематичне рівняння швидкості для рівноприскореного руху:

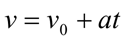
Графік проекції швидкості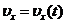

Лінійна залежність проекції швидкості від часу є лінійною функцією .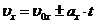

Отже, залежність проекції швидкості від часу — пряма, що розміщується під кутом до осі часу 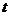і перетинає вісь ординат на відстані 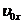від початку координат.

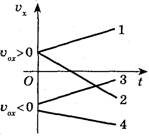
На мал. показані можливі варіанти графічного зображення рівнозмінного руху:

1. рівноприскорений з початковою швидкістю;

2. рівносповільнений з початковою швидкістю;

3.рівноприскорений з початковою швидкістю проти координатної вісі;

4.рівноприскорений з початковою швидкістю проти координатної вісі.

Переміщення та координати

Для встановлення функціональної залежності шляху від часу скористаємось властивістю графіка швидкості, а саме тим, що площа фігури, обмеженої графіком швидкості, перпендикулярами, опущеними з графіка на вісь Ot, та віссю Ot чисельно рівна шляху, який пройшло тіло за визначений проміжок часу (рис 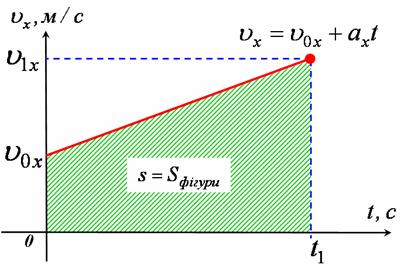2).

мал. 2

Для прикладу візьмемо графік прямолінійного рівноприскореного руху вздовж осі ОХ. Як видно з рисунка, фігура утворена графіком, віссю Ot та перпендикулярами, опущеними з визначеної точки на графіку до осі Ot – це трапеція. З геометрії відомо, що площа трапеції дорівнює добутку півсуми основ на висоту, тобто:

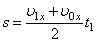(1)

Рівняння проекції швидкості при рівноприскореному русі має вигляд 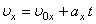(2). Отже, проекцію миттєвої швидкості 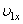можна знайти використовуючи рівняння (2):

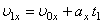(3)

Підставимо значення 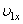у формулу (1):

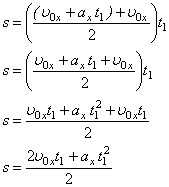
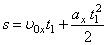(4)- рівняння шляху.

Отже, ми отримали рівняння шляху для рівнозмінного руху. Якщо врахувати, що шлях, пройдений тілом вздовж координатної осі, можна знайти, як відстань між двома точками, тоді 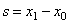(5) (де 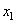- миттєва координата тіла; 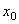- початкова координата тіла). З врахуванням (5) рівняння (4) набуде вигляду:

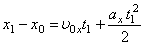
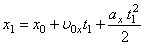(6) – рівняння руху

Ми отримали рівняння, яке дає можливість знайти координату тіла у буд-який момент часу . Як видно з рівняння (6) залежність координати тіла від часу є квадратичною, отже, графіками залежностей проекції переміщення і координати є параболи, вітки яких згідно з параметрами руху мають різний вигляд .

S = v 2 − v 0 2 2 a {\displaystyle S={\frac {v^{2}-v_{0}^{2}}{2a}}} Графіки проекції переміщення 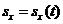та координати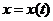

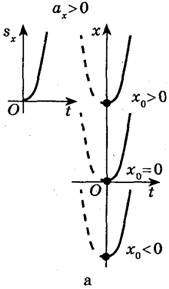
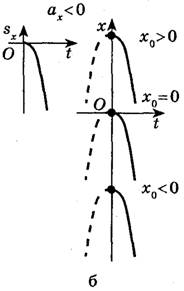
мал.3(а,б)

Вільне падіння

Цікавими прикладами прямолінійного рівноприскореного руху, що спостерігається у природі, є рух тіла, кинутого вертикально вгору. Як свідчить досвід, це тіло з часом все ж таки впаде на Землю. Проаналізував­ши його складний рух, можна зробити висновок, що на першому етапі тіло рухається вгору з від’ємним прискоренням (кожне наступне значення швидкості менше за попереднє), потім на мить зупиняється, змінює на­прям свого руху і починає рухатись рівноприскорено вниз. Цей останній етап руху тіла, кинутого вертикально вгору, називають вільним падінням.