Для студентів-заочників 2 курсу факультету Судноводіння
ВАРІАНТ 0
ЗАДАЧА 1. Точка обертається по колу радіусом R = 1,2 м. Рівняння руху точки j = Аt + Вt3, де А = 0,5 рад/с; В = 0,2 рад/с3. Визначити тангенційне аt, нормальне an і повне а прискорення точки в момент часу і = 4 с.
ЗАДАЧА 2. У дерев'яну кулю масою m1 = 8 кг яка підвішена на нитці довжиною L = 1,8 м влучає куля масою m2 = 4 г, яка летить горизонтально. З якою швидкістю летіла куля, якщо нитка відхилилась від вертикалі на кут a = 3°? Розміром кулі знехтувати. Удар вважати прямим, центральним.
ЗАДАЧА 3. Визначити роботу розтягування двох з'єднаних послідовно пружних жорсткостями k1 = 400 Н/м і k2 = 250 Н/м, якщо перша пружина при цьому розтягнулась на DL = 2 см.
ЗАДАЧА 4. Визначити швидкість поступального руху суцільного циліндра, який скотився з похилої площини висотою h = 20 см.
ЗАДАЧА 5. На краю платформи у вигляді диска діаметром D = 2 м, яка обертається по інерції навколо вертикальної осі з частотою n1 = 8 хв-1, стоїть людина масою m1 = 70 кг. Коли людина перейшла у центр платформи, вона стала обертатись з частотою n2 = 10 хв-1. Визначити масу m2 платформи. Момент інерції людини розраховувати як для матеріальної точки.
ЗАДАЧА 6. Визначити кількість речовини V і число N молекул кисню масою m = 0,5 кг.
ЗАДАЧА 7. Балон об'ємом V = 20 л заповнений азотом. Температура азоту дорівнює 400 К. Коли частину азоту використали, тиск в балоні знизився на Dр = 200 кПа. Визначити масу використаного азоту. Процес вважати ізотермічним.
ЗАДАЧА 8. Визначити показник адіабати g ідеального газу, який при температурі Т = 350 К і тиску р = 0,4 МПа займає об'єм V = 300 л і має теплоємність СV = 857 Дж/К.
ЗАДАЧА 9. При адіабатичному стисканні тиск кисню було збільшено від р1 = 50 кПа до р2 = 0,5 МПа. Потім при незмінному об'ємі температура кисню була знижена до початкової. Визначити тиск р3 газу у кінці процесу.
ЗАДАЧА 10. Визначити роботу А2 ізотермічного стискання газу, який здійснює цикл Карнo, к.к.д. якого h = 0,4, якщо робота ізотермічного розширення дорівнює А1 = 8 Дж.
ЗАДАЧА 11. Точкові заряди Q1 = 20 мкКл і Q2 = -10 мкКл знаходяться на відстані d = 5 см один від одного. Визначити напруженість поля в точці, яка розміщена на відстані r1 = 3 см від першого і r2 = 4 см від другого зарядів. Визначити також силу F, яка діє в цій точці на точковий заряд Q = 1 мкКл.
ЗАДАЧА 12. Пилинка масою m = 20 мкг, яка несе на собі заряд Q = 40 нКл, влетіла в електричне поле у напрямку силових ліній. Після проходження різниці потенціалів U = 200 В пилинка мала швидкість υ = 10 м/с. Визначити швидкість υ0 пилинки до того, як вона влетіла в поле.
ЗАДАЧА 13. Котушка і амперметр з'єднані послідовно і приєднані до опору r = 4 кОм. Амперметр показує силу струму І = 0,3 А, вольтметр – напругу U = 120 В. Визначити опір котушки. Скільки відсотків складе похибка, якщо при визначенні опору котушки не буде враховано опір вольтметра?
ЗАДАЧА 14. Прилад з опором r = 6 Ом підключений до двох паралельно з'єднаних джерел струму з е.р.с. ξ1 = 2,2 В і ξ2 = 2,4 В і внутрішнім опором r1 = 0,8 Ом і r2 = 0,2 Ом. Визначити силу струму в цьому приладі та напругу на затисках другого джерела струму.
ВАРІАНТ 1
ЗАДАЧА 1. Визначити швидкість v і повне прискорення а точки в момент часу t = 2 с, якщо вона рухається по колу радіусом R = 1 м відповідно рівняння руху ξ = Аt + Вt3, де А = 8 м/с; В = -1 м/с3; ξ – криволінійна координата, яка відрахована від якоїсь точки, прийнятої за початкову, вздовж кола.
ЗАДАЧА 2. По невеликому шматку м'якого заліза, який лежить на накувальні масою m1 = 300 кг, б’є молот масою m2 = 8 кг. Визначити к.к.д. η удару, якщо удар не пружний. Корисною вважати енергію, яка пішла на деформацію шматка заліза.
ЗАДАЧА 3. Зі ствола автоматичного пістолета вилетіла куля масою m1 = 10 г зі швидкістю υ = 300 м/с. Затвор пістолета масою т2 = 200 г притискається до ствола пружиною, жорсткість якої k = 25 кН/м. На яку відстань відійде затвор після пострілу? Вважати, що пістолет жорстко закріплений.
ЗАДАЧА 4. Тонкостінний циліндр діаметром основи D = 30 см і масою m = 12 кг обертається відповідно рівнянню φ = А + Вt + Сt, де А = 4 рад; В = -2 рад/с; С = 0,2 рад/с3. Визначити діючий на циліндр момент сил М в момент часу t = 3 с.
ЗАДАЧА 5. На кінці нерухомої лавки Жуковського діаметром D = 0,8 м і масою m1 = 6 кг стоїть людина масою m2 = 60 кг. З якою кутовою швидкістю почне обертатись лавка, якщо людна зловить м'яч, який на неї летить масою m = 0,5 кг? Траєкторія м'яча горизонтальна і проходить на відстані r = 0,4 м від осі лавки. Швидкість м'яча υ = 5 м/с.
ЗАДАЧА 6. Скільки атомів міститься у ртуті: 1) кількістю речовини n = 0,2 моль; 2) масою m = 1 г?
ЗАДАЧА 7. У балоні об'ємом V = 15 л знаходиться аргон під тиском р1 = 600 кПа при температурі Т1 = 300 К. Коли з балона була взята якась кількість аргону, тиск в балоні знизився до р2 = 400 кПа, а температура встановилась Т2 = 260 К. Визначити масу m аргону, взятого з балона.
ЗАДАЧА 8. Визначити відносну молекулярну масу Мr і молярну масу m газу, якщо різниця його питомих теплоємностей СP – СV = 2,08 кДж/(кг × К).
ЗАДАЧА 9. Кисень масою m = 200 г займає об'єм V1 = 100 л і знаходиться під тиском р1 = 200 кПа. При нагріванні газ розширився при постійному тиску до об'єму V2 = 300 л, а потім його тиск виріс до р3 = 500 кПа при незмінному об'ємі. Знайти зміну внутрішньої енергії DU газу, виконану роботу А та теплоту Q, яка передана газу. Побудувати графік процесу.
ЗАДАЧА 10. Газ, який здійснює цикл Карнo, віддав охолоджувачу теплоту Q2 = 14 кДж. Визначити температуру Т1 нагрівача, якщо температура охолоджувача T2 = 280 К, а робота циклу А = 6 кДж.
ЗАДАЧА 11. Три однакових точкових заряди Q1 = Q2 = Q3 = 2 нКл знаходяться у вершинах рівностороннього трикутника зі стороною а = 10 см. Визначити за величиною та напрямом силу F, що діє на один із зарядів збоку двох інших.
ЗАДАЧА 12. Електрон, який має кінетичну енергію Т = 10 еВ, влетів в однорідне електричне поле у напрямку силових ліній поля. Яку швидкість буде мати електрон, пройшовши в цьому полі різницю потенціалів U = 8 В?
ЗАДАЧА 13. Е.р.с. батареї ξ = 80 В, внутрішній опір r1 = 5 Ом. Зовнішній ланцюг споживає потужність Р = 100 Вт. Визначити силу струму l в ланцюгу, напругу U, під якою знаходиться зовнішній ланцюг, та його опір r.
ЗАДАЧА 14. Визначити силу струму у кожному елементі та напругу на затисках реостата (див.рис.), якщо ξ1 = 2 В,r1 = 1 Ом, ξ2 = 6 В, r2 = 1 Ом, r = 200 м.
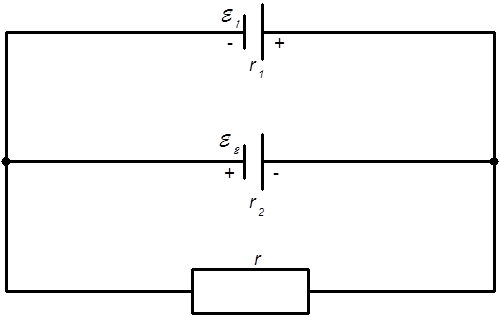
ВАРІАНТ 2
ЗАДАЧА 1. По прямій лінії рухаються дві матеріальні точки згідно рівнянням: х1 = А1 +В1t + С1t2та x2 = А2 +В2t + С2t2, де А1 = 10 м; В1 = 1 м/с; С1 = -2 м/с2; А2 =3 м; В2 = 2 м/с; С2 = 0,2 м/с2. В який момент часу швидкості цих точок будуть однаковими? Знайти прискорення а1 і а2 цих точок в момент t = 3 с.
ЗАДАЧА 2. На візку, який вільно рухається по горизонталі зі швидкістю υ1 = 3 м/с, знаходиться людина. Людина стрибає в бік, протилежний руху візка. Після стрибка швидкість візка змінилася і стала дорівнювати u1 = 4 м/с. Визначити горизонтальну швидкість u2 людини при стрибку відносно візка. Маса візка m1 = 210 кг, маса людини m2 = 70 кг.
ЗАДАЧА 3. Куля масою m1 = 1 кг рухається зі швидкістю υ1 = 4 м/с і стикається з кулею масою m2 = 2 кг, що рухається назустріч їй зі швидкістю υ2 = 3 м/с. Які швидкості u1 і u2 куль після удару? Удар вважати абсолютно пружним, прямим, центральним.
ЗАДАЧА 4. Пружина жорсткістю k = 500 Н/м стиснута силою F = 100 Н. Визначити роботу А зовнішньої сили, додатково стискаючої цю пружину ще на Δl = 2 см.
ЗАДАЧА 5. Людина стоїть на лавці Жуковського і тримає в руках стержень вертикально вздовж осі обертання лавки. Стержень служить віссю обертання колеса, розташованого на його верхньому кінці. Лавка нерухома, колесо обертається з частотою n1 = 15 с-1. З якою кутовою швидкістю ω2 буде обертатися лавка, якщо людина поверне стержень на кут φ = 180° і колесо виявиться внизу? Сумарний момент інерції людини і лавки J = 8 кг ּ м2, радіус колеса R = 25 см. Масу колеса m = 2,5 кг можна рахувати рівномірно розподіленою по ободу. Вважати, що центр мас людини з колесом знаходиться на осі платформи.
ЗАДАЧА 6. Вода при температурі t = 4°С займає об'єм V = 1 см3. Визначити кількість рідини ν і число N молекул води.
ЗАДАЧА 7. Дві посудини однакового об'єму містять кисень. В одній посудині тиск р1 = 2 МПа і температура Т1 = 800 К, в другій р2 = 2,5 МПа, температура Т2 = 200 К. Посудини з'єднали трубкою та охолодили розміщений в них кисень до температури Т = 200 К. Визначити встановлений в посудинах тиск р.
ЗАДАЧА 8. Визначити відносну молекулярну масу Мк і молярну масу μ газу, якщо різниця його питомих теплоємностей СP – СV = 2,08 кДж/(кг ּК).
ЗАДАЧА 9. Об'єм водню при ізотермічному розширенні збільшився в n = 3 рази. Визначити роботу А, яка здійснена газом, та теплоту Q отриману ним при цьому.
ЗАДАЧА 10. Газ, який служить робочою речовиною у циклі Карнo, отримав від нагрівача теплоту Q1 = 4,38 кДж і здійснив роботу А = 2,4 кДж. Визначити температуру нагрівача, якщо температура охолоджувача T2 = 273 К.
ЗАДАЧА 11. Точковi заряди Q1 = 20 мкКл і Q2 = -10 мкКл знаходяться на відстані d = 5 см один від одного. Визначити напруженість поля в точці, яка розміщена на відстані r1 = 3 см від першого і r2 = 4 см від другого зарядів. Визначити також силу F, яка діє в цій точці на точковий заряд Q = 1 мкКл.
ЗАДАЧА 12. Знайти співвідношення швидкостей іонів Сu++ і К+ які пройшли однакову різницю потенціалів.
ЗАДАЧА 13. Від батареї, е.р.с. якої ξ = 600 В потрібно передати енергію на відстань L = 1 км. Потужність споживача Р = 5 кВт. Знайти мінімальні втрати потужності у мережі, якщо діаметр мідного подвійного дроту d = 0,5 см.
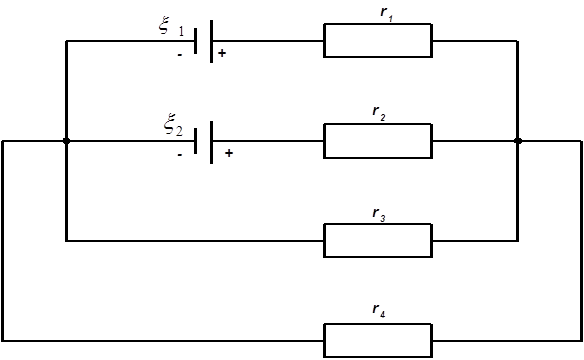
ЗАДАЧА 14. Визначити сили струмів на всіх ділянках електричного ланцюга (див. рис.), якщо ξ1 = 8 В, ξ2 = 12 В, r1 = 1 Ом, r2 = 1 Ом, r3 = 4 Ом, r4 = 2 Ом. Внутрішніми опорами джерел струмів знехтувати.
ВАРІАНТ 3
ЗАДАЧА 1. Визначити повне прискорення а в момент t = 3 с точки, яка знаходиться на ободі колеса радіусом R = 0,5 м, який обертається відповідно рівнянню j = Аt + Вt3 , де А = 2 рад/с; В = 0,2 рад/с3.
ЗАДАЧА 2. Гармата, яка жорстко закріплена на залізничній платформі, виконує постріл уздовж полотна залізної дороги під кутом a = 30° до лінії горизонту. Визначити швидкість u2 відкату платформи, якщо снаряд вилітає зі швидкістю u1 = 480 м/с. Маса платформи з гарматою і снарядами m = 18 т, маса снаряда m1 = 60 кг.
ЗАДАЧА 3. Дві пружини жорсткістю k1 = 0,5 кН/м і k2 = 1 кН/м закріплені паралельно. Визначити потенціальну енергію П даної системи при абсолютній деформації DL = 4 см.
ЗАДАЧА 4. Нитка з прив’язаними до її кінців тягарями масою m1 = 50 г і m2 = 60 г перекинута через блок діаметром D = 4 см. Визначити момент інерції блока, якщо під дією сили тяжіння він отримав кутове прискорення e = 1,5 рад/с2.
ЗАДАЧА 5. На лавці Жуковського стоїть людина і тримає в руках стержень вертикально. Лавка з людиною обертається з кутовою швидкістю w1 = 4 рад/с. З якою кутовою швидкістю w2 буде обертатися лавка з людиною, якщо повернути стержень так, щоб він зайняв горизонтальне положення? Сумарний момент інерції людини і лавки J =5 кг × м2. Довжина стержня L = 1,8 м, його маса т = 6 кг. Вважати, що центр мас стержня з людиною знаходиться на осі платформи.
ЗАДАЧА 6. Знайти молярну масу m масу mм однієї молекули кухонної солі.
ЗАДАЧА 7. Вирахувати густину r азоту, який знаходиться в балоні під тиском р = 2 МПа при температурі Т = 400 К.
ЗАДАЧА 8. В посудині об'ємом V = 6 л знаходиться при нормальних умовах двохатомний газ. Визначити теплоємність СV цього газу при постійному об’ємі.
ЗАДАЧА 9. Водень масою 40 г і температурою Т = 300 К, адіабатично розширився, збільшивши об'єм в n1 = 3 рази. Потім при ізотермічному стисканні об’єм газу зменшився в n2 = 2 рази. Визначити повну роботу А, яка здійснена газом, та кінцеву температуру газу.
ЗАДАЧА 10. Газ, який здійснює цикл Карно, віддав охолоджувачу 67% теплоти, отриманої від нагрівача. Визначити температуру Т2 охолоджувача, якщо температура нагрівача Т1 = 430 К.
ЗАДАЧА 11. Дві однакові заряджені кульки підвішені в одній точці на нитях однакової довжини. При цьому ниті розійшлися на кут a. Кульки занурюються в масло. Яка густина r0 масла, якщо кут розходження ниток при зануренні кульок в масло залишається незмінним? Густина матеріалу кульок r = 1,5 × 103 кг/м3, діелектрична проникність масла e = 2,2.
ЗАДАЧА 12. Електрон з енергією Т = 400 еВ (на нескінченності) рухається уздовж силової лінії у напряму поверхні металевої зарядженої сфери радіусом R = 10 см. Визначити мінімальну відстань а, на яку наблизиться електрон до поверхні сфери, якщо заряд її Q = -10 нКл.
ЗАДАЧА 13. Визначити число електронів, які проходять у секунду через одиницю площі поперечного перерізу залізного дроту довжиною l = 20 м при напрузіна його кінцях U = 16 В.
ЗАДАЧА 14. Два джерела струму ξ1 = 12 В з внутрішнім опором r1 = 4 Ом і ξ2 = 8 В з внутрішнім опором r2 = 2 Ом з'єднані, як показано на рис. Визначити сили струму у провіднику і джерелах струму.
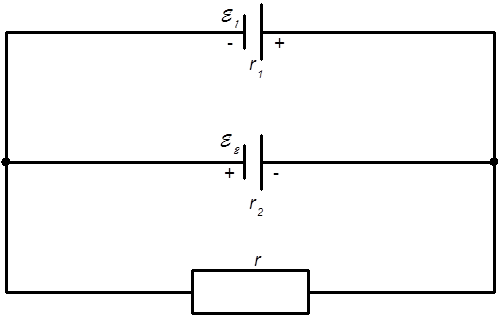
ВАРІАНТ 4
ЗАДАЧА 1. Диск радіусом R = 0,2 м обертається відповідно рівнянню j = А + Вt + Сt3, де А = 3 рад; В = -1 рад/с; С = 0,1 рад/с3. Визначити тангенційне аt , нормальне an і повне а прискорення точок на ободі диска для моменту часу t = 10 c.
ЗАДАЧА 2. На підлозі стоїть візок у вигляді довгої дошки, яка споряджена легкими колесами. На одному кінці дошки стоїть людина. Маса людини m1 = 60 кг, маса дошки m2 = 20 кг. З якою швидкістю u (відносно підлоги) буде рухатись візок, якщо людина піде уздовж його зі швидкістю (відносно дошки) υ = 1 м/с? Масою колес знехтувати, тертя не враховувати.
ЗАДАЧА 3. Яку потрібно виконати роботу А, щоб пружину жорсткістю k = 800 Н/м, стиснуту на х = 6 см, додатково стиснути на Dх = 8 см?
ЗАДАЧА 4. Визначити швидкість поступального руху суцільного циліндра, який скотився з похилої площини висотою h = 20 см.
ЗАДАЧА 5. На кінці нерухомої лавки Жуковського діаметром D = 0,8 м і масою m1 = 6 кг стоїть людина масою т2 = 60 кг. З якою кутовою швидкістю почне обертатись лавка, якщо людна зловить м'яч який на неї летить масою m = 0,5 кг? Траєкторія м'яча горизонтальна і проходить на відстані r = 0,4 м від осі лавки. Швидкість м'яча υ = 5 м/с.
ЗАДАЧА 6. У балоні об'ємом V = 3 л утримується кисень масою m = 10 г. Визначити концентрацію n молекул газу.
ЗАДАЧА 7. У посудині об’ємом V = 40 л знаходиться кисень. Температура кисню Т = 300 К. Коли частину кисню витратили, тиск в балоні знизився на Dр = 100 кПа. Визначити масу витраченого кисню, якщо температура газу в балоні залишилась попередньою.
ЗАДАЧА 8. Трьохатомний газ під тиском р = 240 кПа при температурі 20°С займає об'єм V = 5 л. Визначити теплоємність СР цього газу при постійному тиску.
ЗАДАЧА 9. Кисень масою m = 250 г, який мав температуру Т1 = 200 К, був адіабатно стиснутий. При цьому була здійснена робота А = 25 кДж. Визначити кінцеву температуру Т газу.
ЗАДАЧА 10. Газ, який являється робочою речовиною у циклі Карно, отримав від нагрівача теплоту Q1 = 4,38 кДж і здійснив роботу А = 2,4 кДж. Визначити температуру нагрівача, якщо температура охолоджувача Т2 = 273 К.
ЗАДАЧА 11. Чотири однакових заряди Q1 = Q2 = Q3 = Q4 = 40 нКл закріплені у вершинах квадрата зі стороною а = 10 см. Знайти силу F, яка діє на однин з цих зарядів з боку трьох інших.
ЗАДАЧА 12. Електрон, пройшовши у плоскому конденсаторі шлях від однієї пластини до другої, отримав швидкість v = 10 м/с. Відстань між пластинами d = 8 мм. Знайти: 1) різницю потенціалів між пластинами; 2) поверхневу густину зарядів s на пластинах.
ЗАДАЧА 13. Е.р.с. батареї, ξ = 24 В. Hайбільша сила струму, яку може дати батарея, Imax = 10 А. Визначити максимальну потужність Рmах, яка може виділятися у зовнішньому колі.
ЗАДАЧА 14. Дві батареї (ξ1 = 12 В, r1 = 2 Ом, ξ2 = 24 В, r2 = 6 Ом) і провідник опором r = 16 Ом з'єднані, як показано на рис. Визначити силу струму в батареях і провіднику.
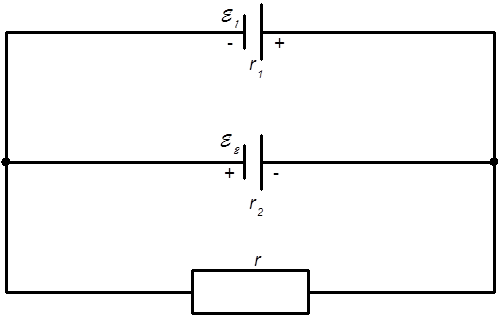
ВАРІАНТ 5
ЗАДАЧА 1. Матеріальна точка рухається прямолінійно. Рівняння руху має вид X = Аt + Вt3 де А = 3 м/с; В = 0,06 м/с3. Знайти швидкість v і прискорення а точки в моменти часу t1 = 0 i t2 = 3 с. Яке середнє значення швидкості < υx > і прискорення < ax > за перші 3 с руху?
ЗАДАЧА 2. Шар масою m1 = 5 кг рухається зі швидкістю υ1 = 1 м/с і зіштовхується з шаром який перебував в спокої масою m2 = 2 кг. Визначити швидкості u1 i u2 шарів після удару. Шари вважати однорідними, абсолютно пружними, удар – прямим, центральним.
ЗАДАЧА 3. Зі ствола автоматичного пістолета вилетіла куля масою m1 = 10 г зі швидкістю υ = 300 м/с. Затвор пістолета масою m2 = 200 г притискається до ствола пружиною, жорсткість якої k = 25 кНм. На яку відстань відійде затвор після пострілу? Вважати, що пістолет жорстко закріплений.
ЗАДАЧА 4. На обід маховика діаметром D = 60 см намотаний шнур, до кінця якого прив'язаний тягар масою m = 2 кг. Визначити момент інерції J маховика, якщо він, обертаючись рівноприскорено під дією ваги тягаря, за час t = 3 с придбав кутову швидкість ω = 9 рад/с.
ЗАДАЧА 5. На краю дископодібної платформи діаметром D = 2 м, яка обертається за інерцією навколо вертикальної осі з частотою n1 = 8 хв-1, стоїть людина масою m1 = 70 кг. Коли людина перейшла в центр платформи, остання стала обертатись з частотою n2 = 10 хв-1. Знайти масу т2 платформи. Момент інерції людини розраховувати як для матеріальної точки.
ЗАДАЧА 6. Визначити кількість рідини n водню, який заповнює посудину об'ємом V = 3 л, якщо концентрація молекул газу в посудині n = 2 × 1018 м-3.
ЗАДАЧА 7. Знайти густину r азоту при температурі Т = 400 К і тиску р = 2МПа.
ЗАДАЧА 8. Розрахувати питомі теплоємності газу, знаючи, що його молярна маса m = 4 × 10-3 кг/моль і відношення теплоємностей СР/СV = 1,67.
ЗАДАЧА 9. Водень масою m = 40 г, який мав температуру Т = 300 К адіабатичнo розширився, збільшивши об'єм у n1 = 3 рази. Потім, при ізотермічному стисканні об'єм газу зменшився в n2 = 2 рази. Визначити повну роботу А, яка здійснена газом, і кінцеву температуру Т газу.
ЗАДАЧА 10. Ідеальна теплова машина працює за циклом Карно. Температура Т1 нагрівача дорівнює 500 К, температура охолоджувача Т2 = 250 К. Визначити термічний к.к.д. h циклу, а також роботу А1, яка здійснена робочою речовиною при ізотермічному розширенні, якщо при ізотермічному стисканні здійснена робота А2 = 70 Дж.
ЗАДАЧА 11. У вершинах квадрата знаходяться однакові заряди Q1 = Q2 = Q3 = Q4 = 8 × 10-10 Кл. Який негативний заряд Q треба помістити у центр квадрата, щоб сила взаємного відштовхування позитивних зарядів була зрівноважена силою притяжіння позитивного заряду?
ЗАДАЧА 12. Пилинка масою m = 5 нг, яка несе на собі N = 10 електронів, пройшла у вакуумі прискорюючу різницю потенціалів U = 1 МВ. Яка кінетична енергія Т пилинки? Яку швидкість v придбала пилинка?
ЗАДАЧА 13. При зовнішньому опорі r1 = 8 Ом сила струму у ланцюгу I1 = 0,8 А, при опорі r2 = 15 Ом сила струму І2 = 0,5 А. Визначити силу струму Ік.з., короткого замикання джерела е.р.с.
ЗАДАЧА 14. Три опори r1 = 6 Ом, r2 = 3 Ом і r3 = 2 Ом, а також джерела з ξ1 = 2,2 В з'єднані, як показано на рис. Визначити е.р.с. ξ джерела, яке треба підключити в ланцюг між точками А і В, так щоб в провіднику опором r3 йшов струм силою І3 = 1 А у напрямі, який показано стрілкою. Опором джерел струму знехтувати.
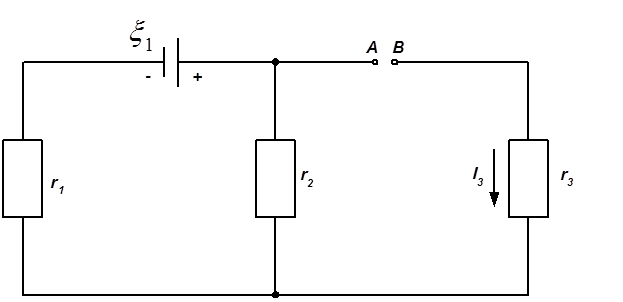
ВАРІАНТ 6
ЗАДАЧА 1. Точка обертається по колу радіусом R = 8 м. В якийсь момент часу нормальне прискорення точки an = 4 м/с2, вектор повного прискорення  утворює в цей момент з вектором нормального прискорення
утворює в цей момент з вектором нормального прискорення  кут a = 600. Знайти швидкість v і тангенційне прискорення аt точки.
кут a = 600. Знайти швидкість v і тангенційне прискорення аt точки.
ЗАДАЧА 2. Два однакових човна масами m = 200 кг кожний (разом з людиною і вантажем, які знаходяться в човнах) рухаються паралельними курсами на зустріч один одному з однаковими швидкостями υ = 1 м/с. Коли човни порівнялись, то з першого човна на другий та з другого на перший одночасно перекидають вантаж масою m1 = 20 кг. Визначити швидкості u1 і u2 човнів після перекидання вантажу.
ЗАДАЧА 3. Яку потрібно виконати роботу А, щоб пружину жорсткістю k = 800 Н/м, стиснуту на х = 6 см, додатково стиснути на Dх = 8 см?
ЗАДАЧА 4. Платформа у вигляді диска діаметром D = 3 м і масою m1 = 180 кг може обертатись навколо вертикальної осі. З якою кутовою швидкістю w1 буде обертатись ця платформа, якщо по її краю пройде людина масою m2 = 70 кг зі швидкістю υ = 1,8 м/с відносно платформи?
ЗАДАЧА 5. По круговій орбіті навколо Землі обертається супутник з періодом Т = 105 хв. Визначити висоту супутника.
ЗАДАЧА 6. Визначити масу mм однієї молекули вуглекислого газу.
ЗАДАЧА 7. Визначити відносну молекулярну масу Мг газу, якщо при температурі Т = 154 К і тиску р = 2,8 МПа він має густину r = 2,8 кг/м3.
ЗАДАЧА 8. Визначити молярні теплоємності газу, якщо його питомі теплоємності СV = 10,4 кДж/(кг × К) і СP = 14,6 кДж/(кг × К).
ЗАДАЧА 9. Азот масою m = 0,1 кг був ізобарнo нагрітий від температури Т1 = 200 К до температури T2 = 400 К. Визначити роботу А, яка здійснена газом, отриману ним теплоту Q та зміну DU внутрішньої енергії азоту.
ЗАДАЧА 10. В скільки разів збільшиться коефіцієнт корисної дії h циклу Карнo при підвищенні температури нагрівача від Т1 = 380 К до T2 = 560 К? Температура охолоджувача Т3 = 280 К.
ЗАДАЧА 11. На відстані d = 20 см знаходяться два точкових заряди Q1 = -50 нКл і Q2 = 100 нКл. Визначити силу F, яка діє на заряд Q3 = -10 нКл, який віддалений від обох зарядів на однакову відстань, яка дорівнює d.
ЗАДАЧА 12. Іон атому літію Li+ пройшов різницю потенціалів U1 = 400 В, іон атому натрію Na+ – різниця потенціалів U2 = 300 В. Знайти співвідношення швидкостей цих іонів.
ЗАДАЧА 13. У мережу з напругою U = 100 В включили котушку з опором r = 2 кОм і вольтметр, які з'єднані послідовно. Покази вольтметра U1 = 80 В. Коли котушку замінили іншою, вольтметр показав U2 = 60 В. Визначити опір другої котушки.
ЗАДАЧА 14. Визначити різницю потенціалів між точками А і В (див. рис.), якщо ξ1 = 8 В, ξ2 = 6 В, r1 = 4 Ом, r2 = 6 Ом, r3 = 8 Ом. Внутрішніми опорами джерел струму знехтувати.
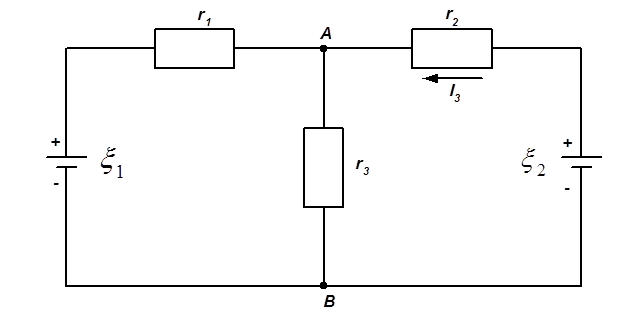
ВАРІАНТ 7
ЗАДАЧА 1. Точка рухається по прямій відповідно рівнянню х = Аt + Вt3, де А = 6 м/с; В = -0,125 м/с3 . Визначити середню швидкість < v > точки в інтервалі часу від t1 = 2 с до t2 = 6 с.
ЗАДАЧА 2. Куля масою m1 = 4 кг рухається зі швидкістю υ1 = 5 м/с і зтикається з кулею масою m2= 6 кг, яка рухається їй на зустріч зі швидкістю υ = 2 м/с. Вважаючи удар прямим, центральним, а кулі однорідними, абсолютно пружними, знайти їх швидкості після удару.
ЗАДАЧА 3. Якщо на верхній кінець вертикально розташованої спіральної пружини покласти тягар, то пружина стиснеться на DL = 3 мм. На скільки стисне пружину той самий тягар, якщо впаде на кінець пружини з висоти h = 8 см?
ЗАДАЧА 4. По горизонтальній плоскій поверхні котиться, диск зі швидкістю υ = 8 м/с. Визначити коефіцієнт опору, якщо диск, будучи представленим самому собі, зупинився, пройшовши шлях S = 18 м.
ЗАДАЧА 5. Платформа, яка має форму диска, може обертатись навколо вертикальної осі. На краю платформи стоїть людина. На який кут повернеться платформа, якщо людина піде уздовж краю платформи і, обійде її, та повернеться у вихідну (на платформі) точку? Маса платформи m1 = 280 гк, маса людини m2 = 80 кг. Момент інерції людини розраховувати як для матеріальної точки.
ЗАДАЧА 6. Визначити концентрацію n молекул кисню, який знаходиться в посудині об'ємом V = 2 л, кількість рідини n кисню дорівнює 0,2 моль.
ЗАДАЧА 7. Знайти густину r азоту при температурі Т = 400 К і тиск р = 2 МПа.
ЗАДАЧА 8. Знайти питомі теплоємності газу, знаючи, що його молярна маса m = 4 × 10-3 кг/моль і відношення теплоємностей СP/СV = 1,67.
ЗАДАЧА 9. Кисень масою m = 250 г, який мав температуру Т1 = 200 К, був адіабатно стиснутий. При цьому була здійснена робота А = 25 кДж. Визначити кінцеву температуру Т газу.
ЗАДАЧА 10. Ідеальна теплова машина працює за циклом Карно. Температура Т1 нагрівача дорівнює 500 К, температура охолоджувача Т2 = 250 К. Визначити термічний к.к.д. h циклу, а також роботу А1, яка здійснена робочою речовиною при ізотермічному розширенні, якщо при ізотермічному стисканні здійснена робота А2 = 70 Дж.
ЗАДАЧА 11. Відстань між двома точковими зарядами Q1 = 2 нКл і Q2 = 4 нКл дорівнює 60 см. Визначити точку, в яку треба помістити третій заряд Q3 так, щоб система зарядів знаходилась у рівновазі. Визначити величину і знак заряду. Стійкою або нестійкою буде рівновага?
ЗАДАЧА 12. При бомбардуванні нерухомого ядра калію a-часткою сила відштовхування між ними досягла F = 100 Н. На яку найменшу відстань наблизилась a-частка до ядра атому калію? Яку швидкість мала a-частка далеко від ядра? Впливом електронної оболонки атому калію знехтувати.
ЗАДАЧА 13. Е.р.с. батареї ξ = 12 В. При силі струму І = 4 А к.к.д. батареї h = 0,6. Визначити внутрішній опір r1 батареї.
ЗАДАЧА 14. Визначити силу струму І3 у провіднику з опором r3 (див. рис.) і напругою U3 на кінцях, якщо ξ1 = 6 В, ξ2 = 8 В, r1 = 4 Ом, r2 = 9 Ом, r3 = 6 Ом. Внутрішніми опорами джерел струму знехтувати.
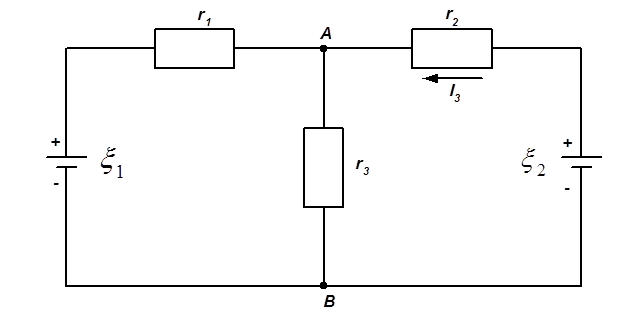
ВАРІАНТ 8
ЗАДАЧА 1. Матеріальна точка рухається прямолінійно. Рівняння руху має вигляд х = Аt + Вt3, де А = 3 м/с; В = 0,06 м/с3. Знайти швидкість v і прискорення а точки в моменти часу t1 = 0 і t2 = 3 с. Яке середнє значення швидкості< υ1 >і прискорення< a1 > за перші 3 с руху?
ЗАДАЧА 2. На підлозі стоїть візок у вигляді довгої дошки, яка споряджена легкими колесами. На одному кінці дошки стоїть людина. Маса людини m1 = 60кг, маса дошки т2 = 20 кг. З якою швидкістю u (відносно підлоги) буде рухатись візок, якщо людина піде уздовж його зі швидкістю (відносно дошки) υ = 1 м/с? Масою колес знехтувати, тертя не враховувати.
ЗАДАЧА 3. З пружинного пістолета з жорсткістю пружини k = 150 Н/м був здійснений постріл кулею m = 8 г. Визначити швидкість v кулі при вильоті її з пістолета, якщо пружина була стиснута на Dх = 4 см.
ЗАДАЧА 4. Кулька масою m = 60 г, прив'язана до кінця нитки довжиною L1 = 1,2 м, обертається з частотою n1 = 2 с-1, спираючись на горизонтальну площину. Нитка укорочується, наближаючи кульку до осі обертання на відстань L2 = 0,6 м. З якою частотою n2 буде при цьому обертатися кулька? Яку роботу А виконує зовнішня сила, скорочуючи нитку? Тертям кульки об площину знехтувати.
ЗАДАЧА 5. Супутник обертається навколо Землі за круговою орбітою на висоті h = 520 км. Визначити період обертання супутника.
ЗАДАЧА 6. Визначити кількість рідини n водню, який заповнює посудину об'ємом V = 3 л, якщо концентрація молекул газу в посудині n = 2 × 1018 м-3.
ЗАДАЧА 7. В балоні об'ємом V = 40 л знаходиться кисень. Температура кисню Т = 300 К. Коли частина кисню була використана, тиск у балоні знизився на Dр = 100 кПа. Визначити масу т використаного кисню, якщо температура газу у балоні залишилась без змін.
ЗАДАЧА 8. Обчислити питомі теплоємності газу, знаючи, що його молярна маса m = 4 × 10-3 кг/моль і відношення молярних теплоємностей СР/СV = 1,67.
ЗАДАЧА 9. У скільки разів збільшиться об'єм водню (n = 0,4 моль) при ізотермічному розширенні, якщо при цьому газ отримає теплоту Q = 800 Дж? Температура водню Т = 300 К.
ЗАДАЧА 10. Газ, який здійснює цикл Карно, отримує теплоту Q1 = 84 кДж. Яку роботу А виконує газ, якщо температура Т1 нагрівача в три рази вища температури T2 охолоджувача?
ЗАДАЧА 11. Дві однакові заряджені кульки підвішені в одній точці на нитях однакової довжини. При цьому ниті розійшлися на кут a. Кульки занурюються в масло. Яка густина r0 масла, якщо кут розходження ниток при зануренні кульок в масло залишається незмінним? Густина матеріалу кульок r = 1,5 × 103 кг/м3, діелектрична проникність масла e = 2,2.
ЗАДАЧА 12. Знайти співвідношення швидкостей іонів Cu++ і K+, які пройшли однакову різницю потенціалів.
ЗАДАЧА 13. Е.р.с. батареї ξ = 80 В, внутрішній опір r1 = 5 Ом. Зовнішнє коло споживає потужність Р = 100 Вт. Визначити силу струму І в колі, напругу U, під якою знаходиться зовнішнє коло, та його опір r.
ЗАДАЧА 14. Три опори r1 = 6 Ом, r2 = 3 Ом і r3 = 2 Ом, а також джерело з ξ1 = 2,2 В з'єднані, як показано на рис. Визначити е.р.с. ξ джерела, яке треба підключити в ланцюг між точками А і В, так щоб в провіднику опором r3 йшов струм силою І3 = 1 А в напрямі, який показано стрілкою. Опором джерел струму знехтувати.
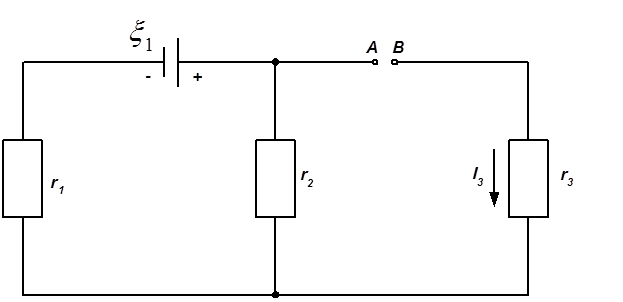
ВАРІАНТ 9
ЗАДАЧА 1. Диск радіусом R = 0,2 м обертається відповідно рівнянню j = А + Вt + Сt3, де А = 3 рад; В = -1 рад/с; С = 0,1 рад/с3. Визначити тангенційне аt, нормальне аn і повне а прискорення точок на ободі диска для моменту часу t = 10 с.
ЗАДАЧА 2. Куля масою т1 = 5 кг рухається зі швидкістю υ1 = 1 м/с і зіштовхується з кулею яка перебуває в спокої масою m2 = 2 кг. Визначити швидкості u1 і u2 куль після удару. Кулі вважати однорідними, абсолютно пружними, удар – прямим, центральним.
ЗАДАЧА 3. Налетівши на пружинний буфер, вагон масою m = 16 т, який рухався зі швидкістю υ = 0,6 м/с, зупинився, стиснувши пружину на DL = 8 см. Знайти загальну жорсткість k пружин буфера.
ЗАДАЧА 4. Блок, який має форму диска масою m = 0,4 кг, обертається під дією сили натягу нитки, до кінців якої підвішені тягарі масою m1 = 0,3 кг і m2 = 0,7 кг. Визначити сили Т1 і T2 натягу нитки по обидві сторони блока.
ЗАДАЧА 5. Визначити лінійну та кутову швидкості супутника Землі, який обертається по колу на висоті 1000 км.
ЗАДАЧА 6. У балоні об'ємом V = 3 л утримується кисень масою m = 10 г. Визначити концентрацію n молекул газу.
ЗАДАЧА 7. Визначити густину r водяної пари, яка знаходиться під тиском р = 2,5 кПа при температурі Т = 250 К.
ЗАДАЧА 8. Одноатомний газ при нормальних умовах займає об'єм V = 5 л. Обчислити теплоємність СV цього газу при постійному об'ємі.
ЗАДАЧА 9. У балоні при температурі Т1 = 145 К і тиску р1 = 2 МПа знаходиться кисень. Визначити температуру Т2 і тиск р2 кисню після того, як з балона буде дуже швидко випущена половина газу.
ЗАДАЧА 10. Здійснюючи цикл Карно, газ отримав від нагрівача теплоту Q1 = 500 Дж і здійснив роботу А = 100 Дж. Температура нагрівача Т1 = 400 К. Визначити температуру T2 охолоджувача.
ЗАДАЧА 11. Два позитивних точкових заряди Q і 9Q закріплені на відстані L = 100 см один від одного. Визначити, в якій точці на прямій, яка проходить через заряди, слід помістити третій заряд так, щоб він знаходився у рівновазі.
Вказати, який знак повинен мати цей заряд для того, щоб рівновага була стійкою, якщо переміщення заряду можливе тільки уздовж прямої, яка проходить через закріплені заряди.
ЗАДАЧА 12. Електрон, який має кінетичну енергію Т = 10 еВ, влетів в однорідне електричне поле у напрямку силових ліній поля. Яку швидкість буде мати електрон, пройшовши в цьому полі різницю потенціалів U = 8 В?
ЗАДАЧА 13. Від батареї, е.р.с. якої ξ = 600 В, потрібно передати енергію на відстань L = 1 км. Потужність споживача Р = 5 кВт. Знайти мінімальні втрати потужності у мережі, якщо діаметр мідного підвідного дроту d = 0,5 см.
ЗАДАЧА 14. Визначити різницю потенціалів між точками А і В (див. рис.), якщо ξ1 = 8 В, ξ2 = 6 В, r1 = 4 Ом, r2 = 6 Ом, r3 = 8 Ом. Внутрішніми опорами джерел струму знехтувати.
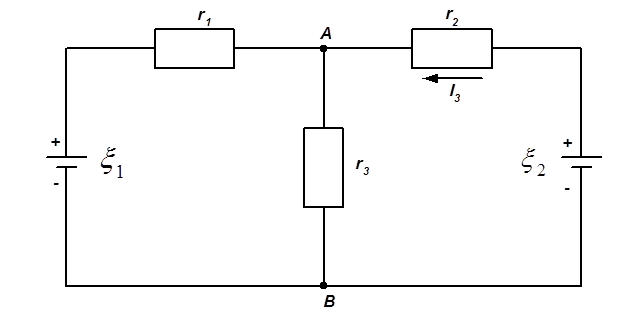
ПРИКЛАДИ РОЗВ’ЯЗУВАННЯ ЗАДАЧ З РОЗДІЛІВ МАГНЕТИЗМ, ОПТИКА, АТОМНА ФІЗИКА
Приклад 1.Два паралельні нескінченно довгі дроти D і С, у яких течуть в одному напрямку електричні струми силою І = 60 А, розміщені на відстані d = 10 см один від одного. Визначити магнітну індукцію  поля, що створюється провідниками зі струмом в точці А (рис. 1), що віддалена від осі одного провідника на відстань r1 = 5 см, від другого – r2 = 12 см.
поля, що створюється провідниками зі струмом в точці А (рис. 1), що віддалена від осі одного провідника на відстань r1 = 5 см, від другого – r2 = 12 см.

Рисунок 1.
Розв’язок. Для знаходження магнітної індукції  в точці А скористаємось принципом суперпозиції магнітних полів. Для цього визначимо напрямок магнітної індукції
в точці А скористаємось принципом суперпозиції магнітних полів. Для цього визначимо напрямок магнітної індукції  і
і 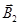 полів, що створюються кожним провідником зі струмом окремо, і складемо їх геометрично:
полів, що створюються кожним провідником зі струмом окремо, і складемо їх геометрично:
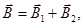
Абсолютне значення магнітної індукції В може бути знайдено за теоремою косинусів:
 (1)
(1)
де a - кут між векторами 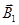 і
і 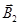 .
.
Значення магнітних індукцій* В1 і В2 виражаються відповідно через силу струму І і відстані r1 і r2 від дротів до точки А:
В1 = m0 І / 2pr1; В2 = m0 І / 2pr2.
Підставляючи вирази В1 і В2 в формулу (1) і виносячи m0 І / 2p за знак кореня, отримаємо:
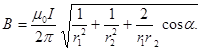 (2)
(2)
Обчислимо cos a. Помітивши, що a = ÐDAC (як кути зі взаємно перпендикулярними сторонами), за теоремою косинусів запишемо 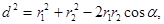 де d – відстань між дротами. Звідси
де d – відстань між дротами. Звідси
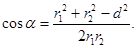
Після підстановки числових значень отримаємо
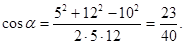
Підставляючи в формулу (2) значення вхідних величин, визначаємо шукану індукцію:
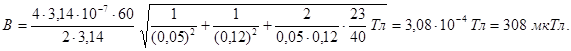
Приклад 2.Електрон, пройшовши прискорюючу різницю потенціалів U = 400 В, потрапив в однорідне магнітне поле напруженістю Н = 103 А/м. Визначити радіус R кривизни траєкторії і частоту n обертання електрону в магнітному полі. Вектор швидкості перпендикулярний до ліній поля.
Розв’язок. Радіус кривизни траєкторії електрона визначимо, виходячи з наступних міркувань: на електрон, що рухається в магнітному полі, діє сила Лоренца 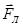 (дією сили тяжіння можна знехтувати). Сила Лоренца перпендикулярна вектору швидкості, отже, вона надає електрону нормальне прискорення. За другим законом Ньютона можна записати FЛ = man, де an – нормальне прискорення або
(дією сили тяжіння можна знехтувати). Сила Лоренца перпендикулярна вектору швидкості, отже, вона надає електрону нормальне прискорення. За другим законом Ньютона можна записати FЛ = man, де an – нормальне прискорення або
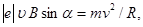 (1)
(1)
де е – заряд електрону;
υ – швидкість електрона;
В – магнітна індукція;
m – маса електрона;
R – радіус кривизни траєкторії;
a – кут між напрямком вектора швидкості 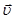 і вектором
і вектором  (в даному випадку
(в даному випадку 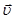 ^
^  і a = 900, sin a = 1).
і a = 900, sin a = 1).
З формули (1) знайдемо
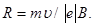 (2)
(2)
Імпульс mυ, що входить в рівняння (2) може бути виражений через кінетичну енергію Т електрона:
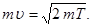 (3)
(3)
Але кінетична енергія електрона, що пройшов прискорюючу різницю потенціалів U, визначається рівнянням
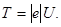
Підставивши цей вираз Т в формулу (3), отримаємо
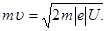
Магнітна індукція В може бути виражена через напруженість Н магнітного поля в вакуумі:
В = m0 Н,
де m0 – магнітна стала.
Підставивши знайдені вирази В і mυ в формулу (2), визначимо
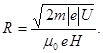 (4)
(4)
Виразимо всі величини, що входять в формулу (4), в одиницях СІ: m = 9,11 × 10-31 кг (із довідкової таблиці 17), 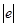 = 1,60 × 10-19 Кл, U = 400 В, m0 = 4p × 10-7 Гн/м, Н = 103 А/м. Підставимо ці значення в формулу (4) і обчислимо:
= 1,60 × 10-19 Кл, U = 400 В, m0 = 4p × 10-7 Гн/м, Н = 103 А/м. Підставимо ці значення в формулу (4) і обчислимо:
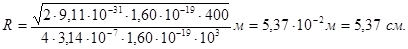
Для визначення частоти обертання n скористаємось формулою, що зв’язує частоту зі швидкістю і радіусом:
n = υ / 2p R. (5)
Підставивши в формулу (5) вираз (2) для радіуса кривизни, отримаємо
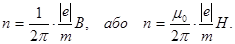
Всі величини, що входять в цю формулу, раніше були виражені в одиницях СІ. Підставимо їх і проведемо обчислення:
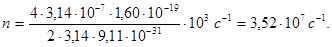
Приклад 3.Від двох когерентних джерел S1 та S2 (l = 0,8 мкм) промені падають на екран. На екрані спостерігається інтерференційна картина. Коли на шляху одного з променів перпендикулярно до нього помістили мильну плівку (n = 1,33), інтерференційна картина змінилась на протилежну. При якій найменшій товщині dmin плівки це можливо?
Розв’язок. Зміна інтерференційної картини на протилежну означає, що та тих ділянках екрана, де спостерігались інтерференційні максимуми, стали спостерігатися інтерференційні мінімуми. Така зміна інтерференційної картини можлива при зміні оптичної різниці ходу променів на непарне число половин довжин хвиль, тобто,
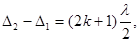 (1)
(1)
де D1 – оптична різниця руху променів до внесення плівки;
D2 – оптична різниця ходу тих самих променів після внесення плівки;
k = 0, ± 1, ± 2, ... .
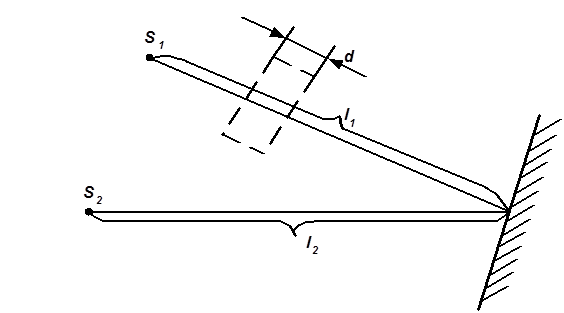
Рисунок 2.
Найменша товщина dmin плівки відповідає k = 0. При цьому формула (1) буде мати вид
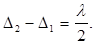 (2)
(2)
Виразимо оптичні різниці ходу D2 та D1. Із рис. 2 виходить:
D1 = l1 – l2,
D2 = [(l1 – dmin) + ndmin] – l2 = (l1 – l2) + dmin (n – 1).
Підставимо вирази D2 та D1 в формулу (2):
(l1 – l2) + dmin (n – 1) - (l1 – l2) = 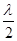 ,
,
або
dmin (n – 1) = 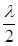 .
.
Звідси

Підставивши числові значення, знайдемо
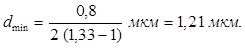
Приклад 4.На дифракційну гратку у напрямку нормалі до її поверхні падає монохроматичне світло. Період гратки d = 2 мкм. Якого найбільшого порядку дифракційного максимуму надає ця гратка у випадку червоного (l1 = 0,7 мкм) та у випадку фіолетового (l2 = 0,41 мкм) світла?
Розв’язок. На підставі відомої формули дифракційної гратки запишемо вираз порядку дифракційного максимуму:
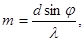 (1)
(1)
де d – період гратки;
j - кут між напрямком на дифракційний максимум і нормаллю до гратки;
l - довжина хвилі монохроматичного світла.
Так як sin j не може бути більшим за 1, то, як це слідує з формули (1), число m не може бути більшим d / l, тобто
m £ d / l. (2)
Підставивши у формулу (2) числові значення, знайдемо:
для червоних променів m £ 2 / 0,7 = 2,86;
для фіолетових променів m £ 2 / 0,41 = 4,88.
Якщо враховувати, що порядок максимумів є цілим числом, то для червоного світла mmax = 2 і для фіолетового mmax = 4.
Приклад 5.Природній промінь світла падає на поліровану поверхню скляної пластини, яка розміщена в рідині. Відбитий від пластини промінь світла утворює кут j = 970 з променем, який падає (рис. 3) Визначити показник заломлення n1 рідини, якщо відбитий промінь світла максимально поляризований.
Розв’язок. Згідно закону Брюстера, промінь світла, відбитий від діелектрика, максимально поляризований в тому випадку, якщо тангенс кута падіння чисельно дорівнює відносному показнику заломлення: tg i1 = n21, де n21 – показник заломлення другого середовища (скла) відносно першого (рідини).
Відносний показник заломлення дорівнює відношенню абсолютних показників заломлення. Отже, tg i1 = n2 / n1.
Так як кут падіння дорівнює куту відбиття, то і1 = j / 2 і, tg j / 2 = n2 / n1 звідки
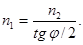
Підставивши числові значення, знайдемо
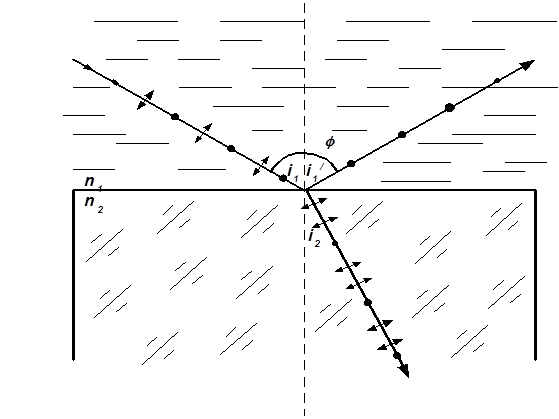
Рисунок 3.
Приклад 6.Два ніколі N1 і N2 розташовані так, що кут між їхніми площинами пропускання a = 600. Визначити, у скільки разів зменшиться інтенсивність l0 природного світла: 1) при проходженні через один ніколь N1; 2) при проходженні через обидва ніколі. Коефіцієнт поглинання світла в ніколі k = 0,05. Втрати на відбиття світла не враховувати.
Розв’язок. Природне світло, яке падає на грань призми ніколя (рис. 4) розщеплюється внаслідок подвійного променезаломлення на два промені: звичайний та незвичайний. Обидва промені однакові за інтенсивностями і повністю поляризовані. Площина коливань незвичайного променя лежить в площині креслення (площина головного перерізу). Площина коливань звичайного променя перпендикулярна площині креслення. Звичайний промінь о внаслідок повного внутрішнього відбиття від межі АВ відбивається на зачорнену поверхню призми і поглинається нею. Незвичайний промінь е проходить крізь призму, зменшуючи свою інтенсивність внаслідок поглинання. Таким чином, інтенсивність світла, яке пройшло крізь першу призму,
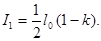
Відносне зменшення інтенсивності світла одержимо, поділивши інтенсивність l0 природного світла, яке падає на перший ніколь, на інтенсивність l1 поляризованого світла:
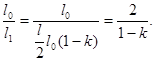 (1)
(1)
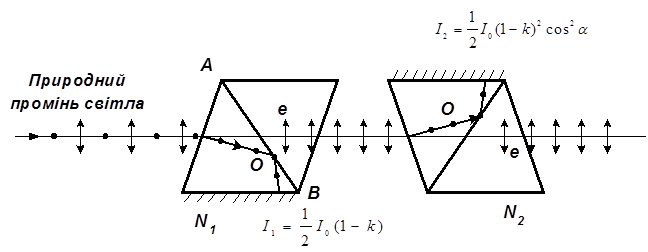
Рисунок 4.
Підставивши в (1) числові значення, знайдемо
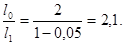
Таким чином, інтенсивність зменшиться в 2,1 рази.
2. Плоскополяризований промінь світла інтенсивності l1 падає на другий ніколь N2 і також розщеплюється на два промені різної інтенсивності: звичайний та незвичайний. Звичайний промінь повністю поглинається призмою, тому інтенсивність його нас не цікавить. Інтенсивність незвичайного променя l2, який вийшов з призми N2, визначається законом Малюса (без урахування поглинання світла у другому ніколі):
l2 = l1 cos2a,
де a – кут між площиною коливань в поляризованому проміні і площиною пропускання
ніколя N2.
Враховуючи втрати інтенсивності на поглинання в другому ніколі, одержимо
l2 = l1 (1 – k) cos2a.
Шукане зменшення інтенсивності при проходженні світла через обидва ніколі знайдемо, поділивши інтенсивність l0 природного світла на інтенсивність l2 світла, яке пройшло систему із двох ніколей:
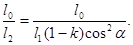
Замінивши відношення l0 / l1 його виразом по формулі (1), одержимо
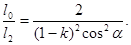
Підставивши дані, проведемо обчислення:
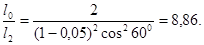
Таким чином, після проходження світла крізь два ніколі інтенсивність його зменшиться в 8,86 рази.
Приклад 7.Довжина хвилі, на яку припадає максимум енергії у спектрі випромінювання абсолютно чорного тіла, l0 = 0,58 мкм. Визначити енергетичну світимість (випромінюваність) Re поверхні тіла.
Рішення. Енергетична світимість Re абсолютно чорного тіла у відповідності з законом Стефана-Больцмана пропорційна четвертому ступеню абсолютної температури і виражається формулою
Re = sT4, (1)
де s – постійна Стефана-Больцмана;
Т – термодинамічна температура.
Температуру Т можна обчислити за допомогою закону зміщення Віна
l0 = b / T, (2)
де b – постійна закону зміщення Віна.
Використовуючи формули (2) і (1) одержимо
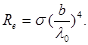 (3)
(3)
Випишемо числові значення величин, які містяться в цій формулі:
s = 5,67 × 10-8 Вт/(м2×К4), b = 2,90 × 10-3 м×К, l0 = 5,8 × 10-7 м, і підставивши числові значення в формулу (3), проведемо обчислення:
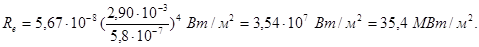
Приклад 8.Визначити максимальну швидкість υmax фотоелектронів, які вириваються з поверхні срібла: 1) ультрафіолетовими променями з довжиною хвилі l1 = 0,155 мкм; 2) g-променями з довжиною хвилі l2 = 1 пм.
Розв’язок. Максимальну швидкість фотоелектронів можна визначити з рівняння Ейнштейна для фотоефекта
e = А + Тmax, (1)
де e – енергія фотонів, які падають на поверхню металу;
А – робота виходу;
Тmax, - максимальна кінетична енергія фотоелектронів.
Енергія фотона обчислюється також за формулою
e = hc / l, (2)
де h – постійна Планка;
с – швидкість світла у вакуумі;
l – довжина хвилі.
Кінетична енергія електрона може бути виражена або класичною формулою
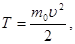 (3)
(3)
або релятивістською
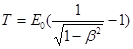 , (4)
, (4)
в залежності від того, яка швидкість надається фотоелектрону. Швидкість фотоелектрона залежить від енергії фотона, який спричиняє фотоефект: якщо енергія e фотона набагато менша за енергію спокою Е0 електрона, то можна застосувати формулу (3), якщо ж e зрівнянна за величиною з Е0, то обчислення за формулою (3) приведе до помилки, тому треба скористатися формулою (4).
1. Обчислимо енергію фотона ультрафіолетових променів за формулою (2):
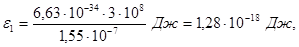
або
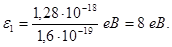
Одержана енергія фотона (8 еВ) набагато менша за енергію спокою електрона (0,51 МеВ). Отже, для даного випадку кінетична енергія фотоелектрона у формулі (1) може бути виражена класичною формулою (3):
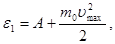
звідки
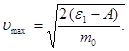 (5)
(5)
Випишемо числові значення величин: e1 = 1,28 × 10-18 Дж (обчислено вище), А = 4,7 еВ = 4,7 × 1,6 × 10-19 Дж = 0,75 × 10-18 Дж , m0 = 9,11 × 10-31 кг.
Підставивши числові значення у формулу (5) знайдемо
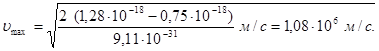
2. Обчислимо енергію фотона g-променів:
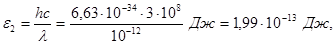
або
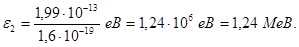
Робота виходу електрона (А = 4,7 еВ) мала у порівнянні з енергією фотона (e2 = 1,24 МеВ), тому можна прийняти що максимальна кінетична енергія електрона дорівнює енергії фотона: Тmax = e2 = 1,24 МеВ. Так як у даному випадку кінетична енергія електрона більша його енергії спокою, то для обчислення швидкості електрона слід взяти релятивістську формулу кінетичної енергії (4). З цієї формули знайдемо
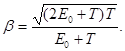
Помітивши, що υ = cb i Tmax = e2 одержимо
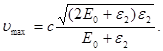
Підставимо числові значення величин і обчислимо:
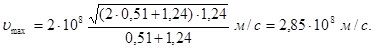
Приклад 9.Електрон в атомі водню перейшов з четвертого енергетичного рівня на другий. Визначити енергію випущеного при цьому фотона.
Розв’язок. Для визначення енергії фотона скористаємося серійною формулою для воднеподібних іонів:
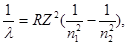 (1)
(1)
де l – довжина хвилі фотона;
R – постійна Ридберга;
