Приклади характерних задач з розв’язанням. Задача 1. Показати, що для квантового КРГ середня енергія системи однозначно виражається через статистичну суму Z:
Задача 1. Показати, що для квантового КРГ  середня енергія системи однозначно виражається через статистичну суму Z:
середня енергія системи однозначно виражається через статистичну суму Z:
.
Розв’язання.З умови нормування для розподілу  маємо
маємо
 ,
,
звідки статистична сума  становить
становить
 . (1)
. (1)
Продиференціюємо цю рівність за  :
:
 .
.
Оскільки середнє значення енергії  за визначенням має вигляд
за визначенням має вигляд
 , (2)
, (2)
порівнюючи (2) з (1), остаточно одержимо
 . (3)
. (3)
Задача 2. Навести графіки розподілу Фермі–Дірака для  :
:
а) за станами;
Б) за енергіями.
Розв’язання. Розподіл середнього числа фермі-частинок 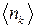 за станами має вигляд
за станами має вигляд
 . (1)
. (1)
 |  | ||
Графік цієї залежності можна зобразити для двох значень параметра
 :
:  та деякого
та деякого  .
.  |
Тут
 - стан, енергія якого дорівнює хімічному потенціалу
- стан, енергія якого дорівнює хімічному потенціалу 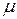 при
при  (енергія Фермі). Відповідний розподіл за енергіями
(енергія Фермі). Відповідний розподіл за енергіями  запишемо так:
запишемо так:  , (2)
, (2)
де  - розподіл числа станів за енергіями, а - незалежна від енергії ε стала. Отже, графік розподілу (2) матиме вигляд:
- розподіл числа станів за енергіями, а - незалежна від енергії ε стала. Отже, графік розподілу (2) матиме вигляд:
 |
Задача 3. Показати, що хімічний потенціал бозе-газу, залишаючись від’ємним, монотонно зменшується з ростом температури.
Розв’язання. Повне число N частинок бозе-газу в об’ємі V можна записати у вигляді
 , (1)
, (1)
де  ;
;  - спін частинок.
- спін частинок.
Продиференціюємо (1) за  при сталому значенні N. Одержимо
при сталому значенні N. Одержимо
 ,
,
звідки
 .
.
Знак правої частини цієї рівності визначається знаком різниці  . Тому при від’ємних
. Тому при від’ємних  маємо
маємо  , тобто, залишаючись від’ємним, хімічний потенціал з ростом температури зменшується.
, тобто, залишаючись від’ємним, хімічний потенціал з ростом температури зменшується.
Задача 4. Показати, що для квантових нерелятивістських ідеальних газів справедлива формула .
Розв’язання. Середня енергія E квантового ідеального газу дорівнює
 , (1)
, (1)
де  для бозе-частинок і
для бозе-частинок і  для фермі-частинок.
для фермі-частинок.
З іншого боку, великий термодинамічний потенціал  , пов’язаний з великою статистичною сумою Z співвідношенням
, пов’язаний з великою статистичною сумою Z співвідношенням  , тобто
, тобто
 . (2)
. (2)
З великого квантового канонічного розподілу маємо
 ,
,
де ni - число частинок в і-му квантовому стані з енергією εi;  .
.
Для бозе-газу (μ від’ємне)
 , (3)
, (3)
для фермі-газу
 . (4)
. (4)
Праві частини рівностей (3) та (4) можна записати як єдиний вираз  , так що (2) матиме вигляд
, так що (2) матиме вигляд
 . (5)
. (5)
Суму за станами в (5) можна замінити інтегруванням за енергією ε, спочатку домноживши праву частину на розподіл  станів за енергіями, що дає
станів за енергіями, що дає
 , (6)
, (6)
де тепер вже  .
.
Інтегруючи (6) за частинами  , одержимо
, одержимо
 . (7)
. (7)
Порівнюючи (7) з (1), остаточно маємо
 , (8)
, (8)
що, до речі, справедливо і для класичних ідеальних газів.
Задача 5. Визначити тиск в електронному газі при Т=0К.
Розв’язання. З формули (1) попередньої задачі при  матимемо (для електронів
матимемо (для електронів  )
)
 , (1)
, (1)
де 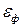 - максимальна енергія електронів при 0 К. Порівнюючи (1) з формулою (8) попередньої задачі, запишемо шуканий тиск Р:
- максимальна енергія електронів при 0 К. Порівнюючи (1) з формулою (8) попередньої задачі, запишемо шуканий тиск Р:
 . (2)
. (2)
Величина 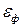 дорівнює хімічному потенціалу при 0 К і становить
дорівнює хімічному потенціалу при 0 К і становить
 , (3)
, (3)
де n - густина частинок. Підставляючи (3) у (2) (з урахуванням, що для електронів  ), остаточно одержимо
), остаточно одержимо
 .
.
