Закон Стефана-Больцмана и закон Вина.

Вначале был установлен теоретически и экспериментально закон зависимости суммарного излучения (энергетической светимости) черного тела от температуры (закон Стефана-Больцмана). Найден весьма точный экспериментальный вид зависимости испускательной способности от частоты и температуры (закон Вина). И, наконец, после ряда неудачных попыток, имеющих огромное значение для понимания вопроса, Планку удалось найти окончательное теоретическое решение задачи. Оно было найдено только путем решительного принципиального изменения основных положений физики, путем создания теории квантов, заложившей принципиально новую базу физической науки. Эта новая теория оказалась столь важной и плодотворной, что дальнейшее развитие ее составило главное содержание теоретической физики на все последующие годы и охватило почти все области науки.

В 1879 г. Стефан на основании анализа собственных измерений и данных других исследователей, пришел к выводу, что энергетическая светимость R любого тела пропорциональна четвертой степени абсолютной температуры. Однако последующие более точные измерения показали ошибочность его выводов.

В 1884 г. Больцман, исходя из термодинамических соображений, теоретически показал, что: энергетическая светимость абсолютно черного тела пропорциональна четвертой степени его термодинамической температуры

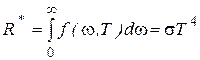, (1.5)

где σ – постоянная. Таким образом, вывод Стефана оказался справедлив лишь для абсолютно черных тел. Тщательные измерения, проведенные позднее для модели абсолютно черного тела, позволили подтвердить выводы Больцмана и определить постоянную σ. По современным измерениям σ = 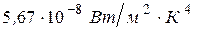. Соотношение между энергетической светимостью абсолютно черного тела и его абсолютной температурой получило название закона Стефана-Больцмана, а константа σ – постоянная Стефана-Больцмана.

В 1893 г. Вин теоретически показал, что 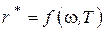должна иметь следующий вид

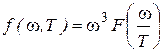(1.6)

где F - некоторая функция отношения ω и Т. И хотя Вину не удалось установить вид функции F , это позволило ему получить ряд важных результатов.

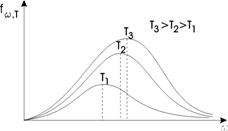Одним из них является закон смещения Вина: частота, соответствующая максимальному значению испускательной способности абсолютно черного тела прямо пропорциональна его термодинамической температуре.

Рис. 1. Распределение энергии в спектре абсолютно черного тела

Из графиков видно, что положение максимума зависимости с повышением температуры смещается в область больших частот согласно закону Вина. Площадь, охватываемая кривой, согласно соотношению (1.5), дает значение энергетической светимости абсолютно черного тела при данной температуре. Видно, что энергетическая светимость сильно возрастает с увеличением температуры, что соответствует закону Стефана-Больцмана. Полученные Вином теоретические результаты полностью согласовывались с результатамиэкспериментов.

В практических целях часто используется другая форма закона смещения Вина: длина волны 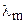, соответствующая максимальному значению испускательной способности абсолютно черного тела, обратно пропорциональна его термодинамической температуре

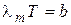.(1.7)

Экспериментальное значение константы b = 2,90∙10^-3 м∙ К.

5. Формула Рэлея-Джинса. Ультрафиолетовая катастрофа.

Окружим излучающее тело идеально отражающей оболочкой. В этом случае излучение, испускаемое телом, не будет рассеиваться по пространству, а, отражаясь стенками, сохранится в пределах полости, и, падая вновь на излучающее тело, поглотится им частично или полностью. Следовательно, будет происходить непрерывный обмен энергией между телом и заполняющим оболочку излучением. Если распределение энергии между телом и излучением остается неизменным для каждой длины волны, состояние системы тело-излучение будет равновесным.

В равновесном состоянии энергия излучения будет распределена в объеме полости с определенной плотностью u = u(T). Спектральной распределение этой энергии можно охарактеризовать функцией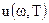

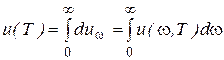(1.8)

где du_ω – доля плотности энергии, приходящаяся на интервал частот dω.

Между равновесной плотностью энергии теплового излучения и испускательной способностью абсолютно черного тела существует следующая связь

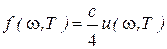, (1.9)

где c – скорость распространения электромагнитной волны в вакууме, т.е. скорость света.

Рэлей в 1900 г. предпринял попытку определить равновесную плотность излучения 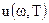с позиций статистической физики, а не термодинамики, как это делали его предшественники. Он рассмотрел равновесное излучение в замкнутой полости с зеркальными стенками как совокупность пространственных стоячих электромагнитных волн. Частоты таких волн должны удовлетворять определенным условиям.

Для простоты поясним на примере одномерного случая: бесконечно протяженные отражающие стенки, между которыми устанавливаются стоячие волны

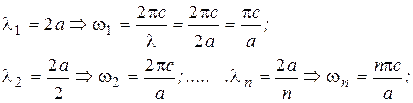
Рэлей показал, что число dn таких частот, находящихся в интервале от ω до ω + dω, пропорционально объему полости V, квадрату частоты ω и ширине интервала dω:

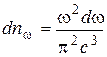. (1.10)

Колебания с разными собственными частотами совершаются независимо друг от друга. Каждой частоте соответствует своя колебательная степень свободы. Применив закон классической статистической физики о равном распределении энергии по всем степеням свободыравновесной системы, Рэлей и Джинс приписали каждому колебанию энергию 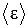= kT. В результате было установлено, что плотность энергии, приходящаяся на интервал частот dω, может быть определена следующим соотношением

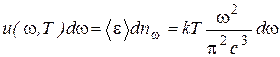(1.11)

Отсюда

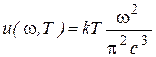(1.12)

Перейдя от плотности энергии к испускательной способности абсолютно черного тела, получим из формулы (1.9)

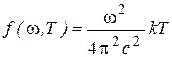(1.13)

Выражения (1.12) и (1.13) называют формулой Релея-Джинса.

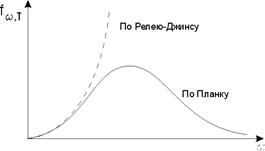Рис.3

Эта формула удовлетворительно согласуется с экспериментальными данными лишь при малых частотах (больших длинах волн) и резко расходится для больших частот (малых длин волн). Интегрирование выражения (1.13) по ω в пределах от 0 до ∞ дает для энергетической светимости тела бесконечно большое значение. Этот результат, получивший название ультрафиолетовой катастрофы, также находится в противоречии с опытом. Расхождение формулы Релея-Джинса с опытом указывало на существование каких-то закономерностей, несовместимых с представлениями классической физики.

Формула Планка

В 1900 г. Планку удалось найти вид функции u(ω,T), в точности соответствующей опытным данным и впервые дать теоретическое обоснование спектральным закономерностям черного излучения.

В своих расчетах Планк выбрал модель излучающей системы в виде совокупности линейных гармонических осцилляторов со всевозможными собственными частотами. Линейный гармонический осциллятор – это система, совершающая гармонические линейные колебания. Гармоническим осциллятором можно назвать: пружинный маятник, математический маятник, колебательный контур, электрический диполь, стоячую волну внутри полости (см. вывод формулы Рэлея-Джинса). По классическим законам излучающий осциллятор может испустить за единицу времени любое количество энергии. При расчете совокупности гармонических осцилляторов, подчиняющимся классическим законам, Планк нашел для функции Кирхгофа, выражение уже известное как формула Рэлея-Джинса. Анализируя полученные результаты, он пришел к выводу, что причина неудачи лежит в неприменимости законов классической физики к атомным осцилляторам, и выдвинул так называемую квантовую гипотезу. Гармонический осциллятор с частотой ω может обладать только таким количеством энергии, в котором содержится целое число элементарных порций ћω.В соответствии с этой гипотезой и излучение осциллятора идет в виде отдельных порций, которые получили название квантов энергии. Величина кванта пропорциональна частоте излучения:

ε = ћ ω.

Коэффициент пропорциональности получил название постоянной Планка. Значение ћ, определенное из экспериментов, равно: ћ = 1,054 ·10 ^-34 Дж · с.

Расчет средней энергии осцилляторов в соответствии с квантовой гипотезой привел к результату

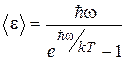(1.14)

Следовательно, для плотности энергии получим выражение

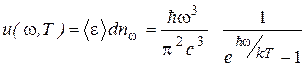, (1.15)

и запишем окончательный вид функции Кирхгофа, полученный Планком

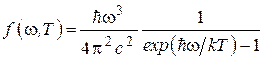. (1.16)

Эта формула точно согласуется с экспериментальными данными во всем интервале частот от 0 до ∞.

В области малых частот (или больших длин волн)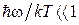

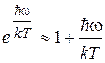
в результате чего формула Планка (1.15) или (1.16) переходит в формулу Рэлея-Джинса (1.12) или (1.13). Это показывает, что в области низких частот теория Планка не противоречит классической теории.

Нетрудно убедиться в том, что формула Планка заключает в себе все упомянутые выше законы теплового излучения абсолютно черного тела, а именно законы Стефана-Больцмана и Вина.

Энергетическую светимость R абсолютно черного тела можно найти интегрированием по частоте:

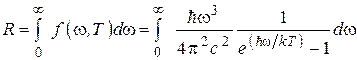
Вычислив интеграл, получим 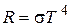. Формула Планка позволяет также вычислить экспериментально найденные константы σ и b, используя универсальные постоянные ħ, k и с.

Таким образом, формула Планка дает исчерпывающее описание равновесного теплового излучения.