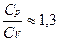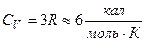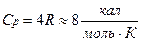Внутрішня енергія ідеального газу.
ТЕПЛОЄМНІСТЬ. КЛАСИЧНА ТЕОРІЯ ТЕПЛОЄМНОСТІ ГАЗІВ
Поняття теплоємності. Теплоємність при різних процесах.
Внутрішня енергія ідеального газу.
Рівняння Майєра.
Політропічні процеси.
Класична теорія теплоємності газів.
Література: [1] стор. 132-147, [2] стор. 103-130, [7] стор. 67-87
· Викладіть основні положення класичної та квантової теорії теплоємностей газів.
· З яких фізичних міркувань випливає, що теплоємність ідеального газу при постійному тиску більша, ніж при постійному об’ємі?
· Чи залежить в загальному випадку теплоємність від потенціальної енергії взаємодії молекул?
Поняття теплоємності. Теплоємність при різних процесах
Досить довго в свідомості вчених існувало поняття про теплород і жила уява про «закон збереження кількості теплоти». Такий стан речей підтримувався завдяки тому, що всі калориметричні досліди проводились або при постійному об’ємі, або при постійному тиску. Справді, якщо об’єм не змінюється, то робота А рівна нулеві і перший закон термодинаміки приймає форму
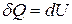 .
.
Якщо постійний тиск, то 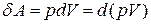 і перший закон термодинаміки
і перший закон термодинаміки
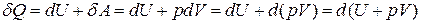 .
.
Величина 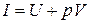 - функція стану, оскільки U, p і V є функціями стану. І називають ентальпією або тепловою функцією. Таким чином, якщо
- функція стану, оскільки U, p і V є функціями стану. І називають ентальпією або тепловою функцією. Таким чином, якщо 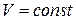 , то приріст кількості теплоти
, то приріст кількості теплоти 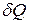 дорівнює зміні внутрішньої енергії, а при
дорівнює зміні внутрішньої енергії, а при 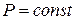 - приросту ентальпії.
- приросту ентальпії.
Тому на основі виконаних дослідів при сталих p або V склалось враження, що 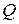 - функція стану, тобто
- функція стану, тобто 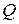 є характеристикою стану тіла і не залежить від шляху, за яким тіло переводиться із стану 1 в стан 2. Перші досліди виконувались із твердими тілами або рідинами, у яких коефіцієнт об’ємного розширення незначний, і тому відмінність природи
є характеристикою стану тіла і не залежить від шляху, за яким тіло переводиться із стану 1 в стан 2. Перші досліди виконувались із твердими тілами або рідинами, у яких коефіцієнт об’ємного розширення незначний, і тому відмінність природи 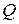 (при
(при 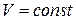 під
під 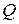 треба розуміти U, при
треба розуміти U, при 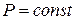 під
під 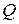 треба розуміти І) залишалась непоміченою. Остаточно
треба розуміти І) залишалась непоміченою. Остаточно 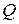 - функція процесу.
- функція процесу.
Теплоємність
Однієї з важливих фізичних величин, що характеризують термодинамічну систему, є теплоємність.
Теплоємність визначає кількість теплоти, що необхідна для зміни температури системи 1 К
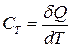 .
.
 Чим більше тіло, тим більшу кількість теплоти необхідно надати, щоб збільшити його температуру на 1 К. Щоб теплоємність характеризувала не тіло, а речовину, використовують теплоємність віднесену до одиниці маси речовини – питому теплоємність
Чим більше тіло, тим більшу кількість теплоти необхідно надати, щоб збільшити його температуру на 1 К. Щоб теплоємність характеризувала не тіло, а речовину, використовують теплоємність віднесену до одиниці маси речовини – питому теплоємність
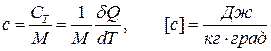 . (1)
. (1)
 Аналогічно визначається фізичний зміст молярної теплоємності
Аналогічно визначається фізичний зміст молярної теплоємності
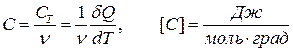 . (2)
. (2)
Молярною теплоємністю називають таку кількість теплоти, яку треба надати 1 молю речовини або відняти у нього, щоб змінити його температуру на 1 градус.
В більшості випадків вважають, що нагріванню або охолодженню підлягає 1 моль речовини, і вираз для молярної теплоємності пишуть у вигляді
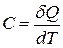 . (3)
. (3)
Виходячи із (1) і (2), запишемо зв'язок між молярною і питомою теплоємностями
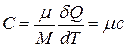 ,
,
де 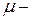 молярна маса речовини.
молярна маса речовини.
Оскільки кількість теплоти 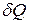 , що необхідна для зміни температури системи на
, що необхідна для зміни температури системи на 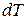 , залежить від характеру процесу, то і теплоємність
, залежить від характеру процесу, то і теплоємність 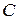 системи також залежить від умов, при яких визначається
системи також залежить від умов, при яких визначається 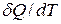 .
. 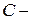 функція процесу: одна і та ж система в залежності від процесу, що відбувається в ней, має різні теплоємності. Обмежень на її значення не накладається, тобто на практиці значення теплоємності пробігають від
функція процесу: одна і та ж система в залежності від процесу, що відбувається в ней, має різні теплоємності. Обмежень на її значення не накладається, тобто на практиці значення теплоємності пробігають від 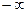 до
до 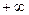 .
.
Перший початок термодинаміки дозволяє знайти значення теплоємностей для різних процесів, а також встановити зв'язок між ними, якщо відомі рівняння стану.
Розглянемо термодинамічну систему, яка характеризується трьома мікроскопічними параметрами p, V, T. Оберемо незалежними параметрами V і T. Тоді внутрішня енергія U, як і третій параметр 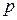 , буде залежати від них
, буде залежати від них
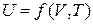 .
.
Повний диференціал функції U
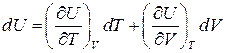 (4)
(4)
Підставивши це значення у перший закон термодинаміки 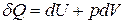 , отримаємо
, отримаємо
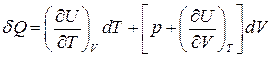 . (5)
. (5)
Тоді формула (3) для молярної теплоємності запишеться
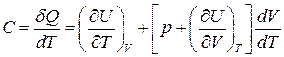 . (6)
. (6)
Використаємо формулу (6) для різних ізопроцесів
I. Ізохорний процес. При сталому об’ємі 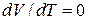 , і формула (6) набуває вигляду
, і формула (6) набуває вигляду
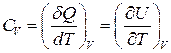 . (7)
. (7)
Тобто, щоб знайти 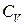 необхідно мати калоричне рівняння
необхідно мати калоричне рівняння 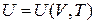 . Навпаки, якщо відома теплоємність
. Навпаки, якщо відома теплоємність 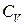 можна із (4) знайти внутрішню енергію
можна із (4) знайти внутрішню енергію
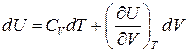
II. Ізобарний процес. Якщо 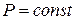 , то відношення
, то відношення 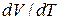 являє собою часткову похідну
являє собою часткову похідну 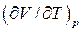 , і співвідношення (6) необхідно переписати
, і співвідношення (6) необхідно переписати
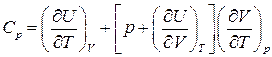 . (8)
. (8)
 Звідси випливає співвідношення для
Звідси випливає співвідношення для 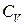 і
і 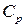 для одного моля будь-якої речовини
для одного моля будь-якої речовини
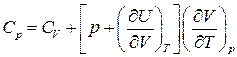 (9)
(9)
З (8) і (9) видно, що для знаходження 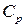 та
та 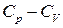 необхідно мати окрім калоричного ще і термічне рівняння (таке, що зв’язує
необхідно мати окрім калоричного ще і термічне рівняння (таке, що зв’язує 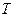 , зовнішні параметри і внутрішній параметр).
, зовнішні параметри і внутрішній параметр).
III. Ізотермічний процес. При сталій температури 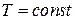 ,
, 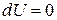 і, отже,
і, отже, 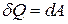 , тобто теплоємність дорівнює нескінченості
, тобто теплоємність дорівнює нескінченості
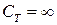 .
.
Внутрішня енергія ідеального газу.
Використаємо отримані співвідношення для ідеального газу. В цьому випадку термічне рівняння являє собою закон Клапейрона-Менделєєва, який для одного моля запишемо
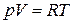
А Колоритне рівняння можна отримати, використовуючи досліди Гей-Люссака та Джоуля-Томсона.
 Дві мідні посудини з однакових об’ємами були з’єднані трубою із краном С. Посудина А була наповнена повітрям, а з В повітря відкачали. При відкриванні крану С повітря з А прямувало в В. При цьому температура в А дещо понижалась, а в В – збільшувалась. Така зміна температури пояснюється тим, що повітря в А при розширені виконувало роботу за рахунок внутрішньої енергії. При досягненні стану термодинамічної рівноваги в А і В встановлювалась температура, рівна початковій.
Дві мідні посудини з однакових об’ємами були з’єднані трубою із краном С. Посудина А була наповнена повітрям, а з В повітря відкачали. При відкриванні крану С повітря з А прямувало в В. При цьому температура в А дещо понижалась, а в В – збільшувалась. Така зміна температури пояснюється тим, що повітря в А при розширені виконувало роботу за рахунок внутрішньої енергії. При досягненні стану термодинамічної рівноваги в А і В встановлювалась температура, рівна початковій.
Проаналізуємо експеримент. Газ знаходиться в жорсткій оболонці, тому зовнішня робота не виконувалась. Кількістю теплоти, що надходила із зовні за час досліду, можна знехтувати. Тому внутрішня енергія повітря повинна залишатись незмінною. Дослід показав, що температура газу залишилась незміною, в той час як об’єм збільшився вдвічі. Звідси можна зробити висновок, що внутрішня енергія газу не залежить від об’єму.
Джоуль повторив дослід в дещо зміненій формі. Повітря в посудині знаходилось під тиском 22 атм. Посудини занурювались у воду, яка переміщувалась під час досліду, щоб температура залишалась всюди постійною. При відкриванні крану С повітря перетікало з А в В, але зміни температури не спостерігались.
Отже для ідеального газу
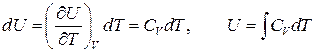 .
.
Дослід показує, що у одноатомних газів 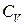 не залежить від
не залежить від 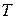 , для інших ідеальних газів існує слабка залежність
, для інших ідеальних газів існує слабка залежність 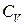 від температури. Якщо
від температури. Якщо 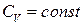 , то ми одразу отримуємо калоричне рівняння
, то ми одразу отримуємо калоричне рівняння
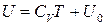 .
.
Рівняння Роберта Майєра
 Оскільки внутрішня енергія ідеального газу не залежить від об’єму
Оскільки внутрішня енергія ідеального газу не залежить від об’єму 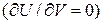 , враховуючи рівняння Клапейрона-Менделєєва (яке дає
, враховуючи рівняння Клапейрона-Менделєєва (яке дає 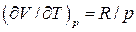 ), для ідеального газу формулу (9) можна записати
), для ідеального газу формулу (9) можна записати
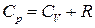 . (10)
. (10)
Дане співвідношення, яке пов’язує молярні теплоємності 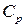 і
і 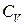 ідеального газу, називається рівнянням Роберта Майєра.
ідеального газу, називається рівнянням Роберта Майєра.
Розділивши (10) на масу одного моля, отримаємо рівняння Майєра для питомих теплоємностей
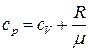 . (11)
. (11)
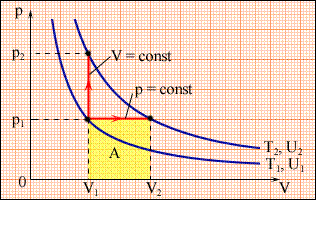 Співвідношення Майєра (10) можна пояснити таким чином. На рисунку приведені ізобарний і ізохорний процеси нагрівання газу на
Співвідношення Майєра (10) можна пояснити таким чином. На рисунку приведені ізобарний і ізохорний процеси нагрівання газу на 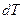 . Якщо об’єм постійний, то теплота йде на підвищення температури на
. Якщо об’єм постійний, то теплота йде на підвищення температури на 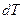 , і новий тиск дорівнює
, і новий тиск дорівнює 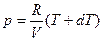 . Якщо дати газу можливість розширятися, то (тиск залишається постійним
. Якщо дати газу можливість розширятися, то (тиск залишається постійним 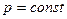 ) газ стане розширюватись і охолоджуватись за рахунок здійснення роботи. Тобто нагрівання в цьому випадку менше, ніж нагрівання при постійному об’ємі
) газ стане розширюватись і охолоджуватись за рахунок здійснення роботи. Тобто нагрівання в цьому випадку менше, ніж нагрівання при постійному об’ємі 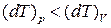 . Тому, щоб нагрівання в процесі при постійному тиску було таким же, необхідно додати більшу теплоту.
. Тому, щоб нагрівання в процесі при постійному тиску було таким же, необхідно додати більшу теплоту.
Таким чином, універсальна газова стала 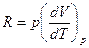 , числено дорівнює роботі, яку виконує 1 моль ідеального газу, розширюючись при нагріванні на 1 К.
, числено дорівнює роботі, яку виконує 1 моль ідеального газу, розширюючись при нагріванні на 1 К.
Політропічні процеси
Рівняння ізотермічного, ізохорного, ізобарного процесів для ідеального газу ми отримали, виходячи лише з рівняння стану ідеального газу. Рівняння ж адіабатного і політропного (із постійною С) процесів не можна отримати, використовуючи лише термічне рівняння, оскільки останнє не включає ані кількість теплоти 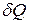 , ані теплоємність С, які визначають ці процеси. Знайдемо ці рівняння, виходячи з першого закону термодинаміки. При політропічному процесі
, ані теплоємність С, які визначають ці процеси. Знайдемо ці рівняння, виходячи з першого закону термодинаміки. При політропічному процесі 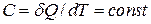 і
і 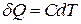 (для адіабатного процесу
(для адіабатного процесу 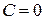 ). Тому для політропи з першого початку термодинаміки маємо
). Тому для політропи з першого початку термодинаміки маємо
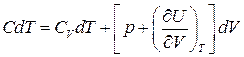 . (12)
. (12)
Звідки, враховуючи (9),

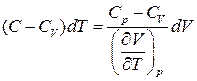
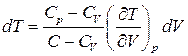 . (13)
. (13)
Це диференціальне рівняння політропи в змінних 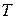 і
і 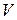 .
.
Щоб перейти до змінних р і 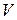 можна із рівняння стану, записаного у вигляді
можна із рівняння стану, записаного у вигляді 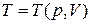 , знайти
, знайти
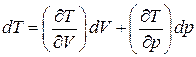
і підставити у попереднє рівняння.
Для того, щоб про інтегрувати рівняння (13), необхідно знати не тільки зв'язок між 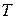 , р і
, р і 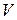 але і вирази для
але і вирази для 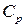 і
і 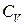 .
.
Давайте розглянемо випадок ідеального газу. Введемо позначення

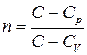 - показник політропи (14)
- показник політропи (14)

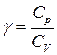 - показник адіабати (14`)
- показник адіабати (14`)
Для ідеального газу 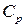 і
і 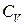 для широкого інтервалу температур не залежить від температури, тому n і
для широкого інтервалу температур не залежить від температури, тому n і 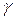 не залежать від температури.
не залежать від температури.
Оскільки 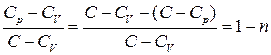 , то (13) перепишеться (врахуємо також
, то (13) перепишеться (врахуємо також 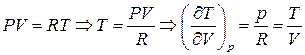 )
)
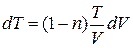 .
.
Яке інтегрується

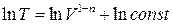

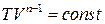 - рівняння політропічного процесу (15)
- рівняння політропічного процесу (15)
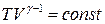 - адіабати. (15`)
- адіабати. (15`)
 Скориставшись рівнянням стану
Скориставшись рівнянням стану 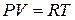 , перепишемо (15) і (15`)
, перепишемо (15) і (15`)

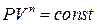 (16)
(16)
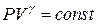 - рівняння Пуасона (16`)
- рівняння Пуасона (16`)
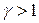 і з (15`) випливає, що при адіабатичному стисненні газ нагрівається. Це явище використовується в дизелях, де горюча суміш загорається при адіабатичному стиснені (див. 7 стор. 76).
і з (15`) випливає, що при адіабатичному стисненні газ нагрівається. Це явище використовується в дизелях, де горюча суміш загорається при адіабатичному стиснені (див. 7 стор. 76).
Порівнюючи рівняння Пуассона 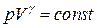 з рівнянням Бойля-Мариотта
з рівнянням Бойля-Мариотта 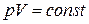 , можна переконатися, що адіабата ідеального газу, побудована в координатах p і V, завжди йде крутіше ізотерми.
, можна переконатися, що адіабата ідеального газу, побудована в координатах p і V, завжди йде крутіше ізотерми.
Це пояснюється тим, що при адіабатному процесі відбувається охолодження газу, в той час як в ізотермічному процесі температура підтримується постійною. Тому при ізотермічному розширенні тиск газу зменшується тільки за рахунок зменшення густини газу, а при адіабатному – за рахунок зменшення густини і середньої кінетичної енергії, тобто температури.
Оскільки адіабата перетинає всі ізотерми даної термодинамічної системи, можливий адіабатичний перехід з однієї ізотерми на іншу, шляхом стискування або розширення газу. А за допомогою ізотермічної зміни об'єму можливий перехід з однієї адіабати на іншу.
Експериментальні дані по теплоємності газів
Порівняємо теоретичні і експериментальні значення Cp і CV для одноатомних газів. Пам’ятаємо, що:
1Дж=0,24кал
1Кал=4,18Дж
Отже, розрахунки дають:
1) 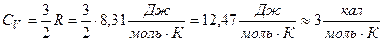
2) 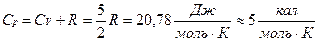
3) 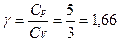
4) 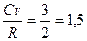
5) 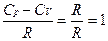
При p порядку атмосферного і нижче і температурах, близьких до кімнатної, експеримент дає:
| одноатомний газ | Cv/R | (Cp-Cv)/R | Cp/Cv |
| гелій | 1,519 | 1,001 | 1,659 |
| неон | - | - | 1,64 |
| аргон | 1,5 | 1,008 | 1,67 |
| криптон | - | - | 1,68 |
| ксенон | - | - | 1,66 |
Експеримент для двохатомних і багатоатомних газів дає такі результати:
| газ | Cv/R | (Cp-Cv)/R | g=Cp/Cv | |
| двохатомні гази | H2, водень | 2,44 | 0,995 | 1,41 |
| HCl, хлористий водень | 2,54 | 1,02 | 1,40 | |
| N2, азот | 2,45 | 1,005 | 1,404 | |
| CO, окис вуглецю | 2,48 | 1,005 | 1,404 | |
| O2, кисень | 2,50 | 1,004 | 1,401 | |
| NO, окис азоту | 2,51 | 1,005 | 1,4 | |
| Cl2, хлор | 3,02 | 1,09 | 1,36 | |
| трьохатомні гази | H2O, пара води | 3,3 | 1,06 | 1,32 |
| CO2, пара вуглекислоти | 3,4 | 1,02 | 1,3 | |
| інші багатоатомні гази | NH4, аміак | 3,42 | 1,06 | 1,31 |
| CH4, метан | 3,25 | 1,01 | 1,31 | |
| C2H4, етилен | 4,04 | 1,03 | 1,25 |
Отже, порівнявши експериментальні значення, можемо багатоатомні гази умовно поділити на дві групи:
1) двохатомні, для яких: 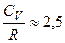 ,
, 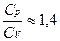
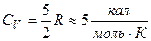
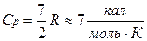
2) гази, молекули яких включають в себе три і більше атомів. Для них:
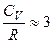 ,
,