Обробка результатів досліду. Середня масова ізобарна теплоємність дослідної рідини визначається за формулою (4.19).

Середня масова ізобарна теплоємність дослідної рідини визначається за формулою (4.19).

Так як під час досліду частина теплоти, яка виділяється електронагрівачем, витрачається на підвищення температури деталей калориметра, повітря в ньому і відводиться від його зовнішніх поверхностей в навколишнє середовище, то до дослідної рідини підводиться теплота:

Q=(1-j)·Qe-Qk, (6.1)

де j - коефіцієнт, який враховує втрати теплоти в навколишнє середовище; Qe - теплота, яка виділяється електронагрівачем, кДж; Q_к -теплота, яка витрачається на нагрів деталей калориметра, кДж. Для даної конструкції калориметра j = 0,016.

Теплота, яка виділяється електронагрівачем:

Q_е = IUt /10³, (6.2)

де I - сила струму в ланцюгу електронагрівника, А; U - спад напруги на електронагрівнику, В; t - час нагрівання рідини від температури t₁ до температури t₂, с.

Теплота, яка витрачається на нагрів деталей калориметра визначається за формулою:

Q_к = C_к DT_к , (6.3)

де C_к - теплоємність калориметра без рідини, кДж/(кг·К); DT - зміна середньої температури деталей калориметра за час t, К.

При обробці дослідних даних прийняти C_к = 1,6 кДж/(кг·К), DT_к = DT.

Результати обчислень слід навести в табличній формі (табл.6.3).

Максимально можливі відносні похибки вимірювання сили струму, спаду напруги, температури визначаються за формулами наведеними в табл.6.4.

Максимально можлива відносна похибка визначення середньої масової ізобарної теплоємності рідини рівна:

dCpm = ± (½dQ½+½dm½+½dDT½), (6.4)

де dQ - максимально можлива відносна похибка визначення теплоти, яка витрачається на нагрівання рідини, %; dm - відносна похибка визначення маси дослідної рідини в калориметрі, %; dDT - максимально можлива похибка визначення зміни температури рідини, %.

Результати оцінки точності досліду представити в табличній формі (табл.6.4).

Порівняйте одержані дослідним шляхом значення Cpm із значенням з довідкових таблиць [2], знайдіть відносну похибку і поясніть причини такого розходження.

Теоретичні відомості і контрольні питання наведенні в лабораторній роботі №4.

Таблиця 6.3 – Обробка результатів досліду

Позначення величин	Одиниця величини	Розрахункова формула	Значення величини
ρо	кг/м3	–
μ	кг/кмоль	–
ΔТ	К	t2 – t1
Qe	кДж	IUτ/103
Qk	кДж	CkΔT
Q	кДж	(1-φ)Qe-Qk
Cpm	кДж/(кг·К)	Q/(mΔT)
C’pm	кДж/(м3·К)	ρoCpm
Cμpm	кДж/(кмоль·К)	μCpm

Таблиця 6.4 – Відносні похибки величин

Позначення похибки величини	Розрахункова формула	Значення похибки, %
δm	–	±1,0
δCk	–	±0,5
δτ	–	±0,3
δI	INKI/I
δU	UNKU/U
δt1	tNKT/t1
δt2	tNKT/t2
δΔT	(t1δt1+ t2δt2)/ΔT
δQk	δCk+δΔT
δQe	δI+δU+δτ
δQ	(QeδQe+QkδQk)/Q
δCpm	δQ+δm+δΔT

7 Лабораторна робота № 8

Визначення коефіцієнта тепловіддачі від горизонтальної

труби до повітря при природній конвекції

Мета і задачі роботи

Метою роботи є засвоєння та поглиблення знань з тепловіддачі при природній конвекції в необмеженому просторі.

Задачі:

- експериментальне визначення середнього коефіцієнта тепловіддачі;

- засвоєння основних понять і залежностей теорії конвективного теплообміну;

- вивчення методики експериментального визначення коефіцієнта тепловіддачі;

- набуття навиків проведення теплотехнічного експерименту, обробки дослідних даних і оцінки похибок вимірювання.

Теоретичні положення

При роботі механізмів, машин та іншого промислового обладнання їх деталі можуть значно нагріватися як за рахунок тертя, так і за рахунок тепла, що підводиться від газів, рідин або інших деталей. В цих процесах важливу роль відіграє конвективний теплообмін.

Конвективним теплообміном (тепловіддачею) називається процес перенесення теплоти від поверхні твердого тіла до рідкого (газового) середовища або навпаки. При цьому перенесення теплоти здійснюються одночасно дією теплопро-відності і конвекції.

Процес переносу теплоти конвекцією нерозривно зв’язаний з переносом самого середовища. Тому конвекція можлива лише в рідинах і газах, частини яких можуть легко перемішуватися.

За природою виникнення розрізняють два види конвекції - вільну і вимушену. Вільною називається конвекція, яка відбувається внаслідок різниці густин нагрітих і холодних частин рідини під впливом фізичного поля (гравітаційного, магнітного, електричного). Виникнення і інтенсивність вільної конвекції визначаються тепловими умовами процесу і залежать від роду рідини, різниці температур. Вимушеною конвекцією називається рух, що виникає під дією сторонніх збудників, наприклад насоса, вентилятора, вітру і інші. В загальному випадку поряд з вимушеною конвекцією одночасно може розвиватися і вільна конвекція. Відносний вплив останньої тим більше, чим більша різниця температур в окремих точках рідини і чим менша швидкість вимушеної конвекції.

Інтенсивність конвективного теплообміну характеризу-ється коефіцієнтом тепловіддачі a, який визначається за формулою Ньютона-Ріхмана:

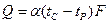, (7.1)

де Q - тепловий потік, Вт; a - коефіцієнт тепловіддачі, Вт/(м²×К); F - площа поверхні теплообміну, м²; (t_C - t_P) - різниця температур стінки і рідини, К.

Коефіцієнт тепловіддачі дорівнює кількості теплоти, яка передається за одиницю часу через одиницю поверхні при різниці температур між поверхнею і рідиною, рівною одному градусу:

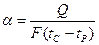. (7.2)

В загальному випадку коефіцієнт тепловіддачі може змінюватися вздовж поверхні теплообміну, і тому розрізняють середній по поверхні коефіцієнт тепловіддачі і місцевий (локальний) коефіцієнт тепловіддачі, який відноситься до одиниці площі поверхні.

Процеси тепловіддачі нерозривно зв’язані з умовами руху рідини. Як відомо, існують два основних режими течії: ламінарний і турбулентний.

Оскільки в інженерній практиці у більшості випадків значення F і (t_C-t_P) задані чи можуть бути порівняно просто визначені, то вирішення головної задачі теплообміну зво-диться до знаходження коефіцієнта тепловіддачі a.

Коефіцієнт тепловіддачі a є функцією багатьох чинників: швидкості руху теплоносія w, температури поверхні нагріву t_C, температури рідини t_P, коефіцієнтів теплопровідності l та температуропровідності a, питомої ізобарної теплоємності С_P, в’язкості v, коефіцієнта об’ємного розширення b і густини теплоносія r, форми Ф та характерних розмірів поверхні теплообміну (l₁,l₂,..., l_n). Через це коефіцієнт тепловіддачі не є фізичною характеристикою речовини:

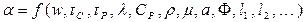. (7.3)

Коефіцієнт теплопровідностіl характеризує здатність речовини проводити теплоту.

Коефіцієнт температуропровідності a=l/c_Рr характеризує швидкість зміни температури в тілі.

Коефіцієнт об’ємного розширення b характеризує відносну зміну об’єму при зміні температури на один градус (при постійному тиску):

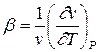, (7.4)

де v - питомий об’єм, м³/кг.

Для газів температурний коефіцієнт об’ємного розширення визначається за формулою:

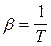(7.5)

Тепловіддача описується системою диференціальних рівнянь в частинних похідних і умовами однозначності з великою кількістю змінних, тому розв’язок цієї системи відносно a чисто аналітичним шляхом неможливий. На практиці використовується напівемпіричний метод, який грунтується на використанні експериментальних даних і теорії подібності.

На основі теорії подібності утворюють комплекси величин (числа подібності), кількість яких значно менша кількості змінних, які описують фізичне явище, а це значно спрощує дослідження процесу. Крім того, теорія подібності встановлює умови при яких результати лабораторних досліджень можна поширити на інші явища, подібні до досліджуваного.

Основні положення теорії подібності можна сформулювати у вигляді трьох теорем.

Перша теорема подібності дає відповідь на питання, які величини треба вимірювати, щоб встановити подібність явищ. В загальній формі ця теорема формулюється так: подібні між собою процеси мають одинакові числа подібності.

На основі другої теореми подібності залежність між змінними, які характеризують будь-який процес, може бути представлена у вигляді залежності між числами подібності К₁, К₂, ..., К_n:

f(К₁, К₂, ..., К_n)=0. (7.6)

Дана залежність називається рівнянням подібності. Так як для всіх подібних між собою процесів числа подібності зберігають одне і те ж значення, то рівняння подібності для них також одинакові.

Можлива і зворотня постановка питання: які умови необхідні і достатні, щоб процеси були подібними. На таке запитання дає відповідь третя теорема подібності, яка формулюється так: подібні ті процеси, умови однозначності яких подібні, і числа подібності, складені з цих величин, і, які входять в умови однозначності, мають одинакові числові значення.

Теорія подібності дозволяє, не інтегруючи диференціальні рівняння, отримати з них числа подібності і, використовуючи дослідні дані, встановити рівняння подібності, які справедливі для всіх подібних між собою процесів.

Числа подібності (критерії подібності) отримують шляхом приведення до безрозмірного виду рівнянь, які описують досліджуване явище. Для стаціонарної тепловіддачі використовують такі числа подібності: Pr (Прандтля), Re (Рейнольдса), Gr (Грасгофа), Nu (Нуссельта). Інколи використовують похідні числа подібності: Пекле Pe=PrRe, Стантона St=Nu/Pe, Релея Ra=PrGr.

Результати лабораторних досліджень тепловіддачі звичайно подають у вигляді рівняння подібності Nu=f(Re,Pr,Gr). Число Нуссельта містить невідому величину (коефіцієнт тепловіддачі a) і є безрозмірним комплексом, що визначається. Числа Re, Pr, Gr, Pe, Ra - визначаючі числа подібності.

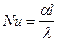- критерій Нуссельта, характеризує конвективний теплообмін між рідиною (газом) і поверхнею твердого тіла;

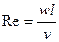- критерій Рейнольдса, характеризує гідродина-мічний режим руху рідини та встановлює свідношення сил інерції до сил в’язкості;

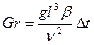- критерій Грасгофа, встановлює співвідно-шення підіймальної сили і сили тяжіння та застосовується для характеристики процесів передачі теплоти при русі рідини, яка виникає внаслідок різниці густин в різних її частинах;

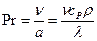- критерій Прандтля, характеризує фізичні властивості рідини та їх вплив на конвективні явища;

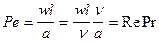- критерій Пекле, є мірою спів-відношення молекулярного і конвективного перенесення теплоти і використовується для характеристики процесів передачі теплоти конвекцією і теплопровідністю.

У формулах критеріїв прийняті наступні позначення: a - коефіцієнт тепловіддачі, Вт/(м²×К); l - визначальний лінійний розмір, м; l - коефіцієнт теплопровідності, Вт/(м×К); w - швидкість потоку рідини, м/с; m - коефіцієнт динамічної в’язкості, м²/с; с_Р - питома теплоємність при постійному тиску, Дж/(кг×К); r - густина рідини, кг/м³; a - коефіцієнт температуропровідності, м²/с; b - температурний коефіцієнт об’ємного розширення, К^-1; Dt=(t_c-t_p) - температурний напір, К.

За відомим значенням критерія Нуссельта Nu коефіцієнт тепловіддачі визначається за формулою:

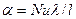, (7.7)

При узагальненні дослідних даних важливим є питання про вибір визначального розміру. В якості такого доцільно прийняти розмір, яким визначається розвиток процесу. Наприклад, при конвективному теплообміні в круглих трубах в якості визначального розміру вибирається їх діаметр. Для каналів неправильного і складного перерізу доцільно брати еквівалентний діаметр, рівний чотирьохкратній площі поперечного перерізу каналу, поділеній на повний змочений периметр перерізу (незалежно від того, яка частина цього периметру приймає участь в теплообміні). При поперечному обтіканні труби і пучка труб в якості визначального розміру береться зовнішній діаметр труби, а при обтіканні плити - її довжина за напрямком руху.

Формула (7.7) використовується для розрахунку тепловіддачі в необмеженому просторі. При тепловіддачі у вузьких каналах і щілинах тепловий потік розраховують за формулами теплопровідності, використовуючи еквівалентний коефіцієнт теплопровідності.

Є декілька методів експериментального визначення середнього коефіцієнта тепловіддачі:

- метод стаціонарного теплового потоку;

- метод нестаціонарного теплового потоку;

- метод регулярного режиму;

- метод квазістаціонарного режиму нагрівання.

В даній роботі використовується метод стаціонарного потоку через циліндричну поверхню. Тому до складу лабораторної установки повинні входити елементи, які забезпечують створення, підтримання незмінним та вимірювання теплового потоку Q через досліджувану поверхню площею F, а також визначення температурного напору DT.