Элементы квантовой теории электропроводности полупроводников

Полупроводниками являются вещества, у которых при 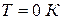валентная зона заполнена электронами полностью, а ширина запрещенной зоны не превышает 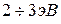(обычно не более 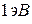) (рис. 8, а). Название «полупроводники» обусловлено тем, что по величине электропроводности эти вещества занимают промежуточное положение между металлами и диэлектриками. Однако характерной особенностью полупроводников является то, что их электрическое сопротивление падает с увеличением температуры, а не растет, как у металлов (6).

Различают собственные и примесные полупроводники. К собственным относится ряд чистых химических элементов (германий Ge, кремний Si, селен Se и др.), а также химические соединения (арсенид галлия GaAs, антимонид индия InSb, карбид кремния SiC и др.). Содержание примесей в них не превышает 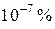. К примесным относят полупроводники с искусственно введенными примесями, которые и определяют их электрические свойства. Поэтому различают собственнуюи примеснуюпроводимости полупроводников. Рассмотрим собственную проводимость полупроводников.

Как уже говорилось выше, собственный полупроводник при 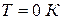представляет собой изолятор (рис. 8, а). При температуре выше абсолютного нуля в результате теплового возбуждения часть электронов верхних уровней валентной зоны переходит на нижние уровни зоны проводимости (рис. 8, б). Электроны, частично заполняющие зону проводимости, будут находиться в условиях, аналогичных тем, в которых находятся электроны, частично заполняющие валентную зону (зону проводимости) в металле (рис. 11). Если в таком полупроводнике создать электрическое поле, то энергии, сообщаемой этим полем электронам, окажется достаточно для того, чтобы переводить электроны, расположенные у дна зоны проводимости, на более высокие свободные энергетические уровни. Эти переходы будут эквивалентны приобретению электронами скорости упорядоченного движения против электрического поля в кристалле полупроводника, т.е. возникновению электрического тока. Проводимость, обусловленная электронами, появившимися в зоне проводимости полупроводника, называется электронной.

Но электроны, переброшенные в зону проводимости из валентной зоны, освобождают в последней такое же количество мест на верхних энергетических уровнях. В результате у потолка валентной зоны появляются энергетические уровни, занятые электронами лишь частично (рис. 8, б). Появление частично занятых уровней позволяет электронам в валентной зоне под действием внешнего электрического поля в полупроводнике переходить с нижележащих уровней на вакантные места верхних уровней, что эквивалентно приобретению ими скорости упорядоченного движения против поля. Эти переходы носят характер эстафеты: электрон переходит с нижнего уровня на свободное место верхнего уровня, на освободившееся место на нижнем уровне переходит электрон с еще более низкого уровня и т.д. На рис. 13, а показана схема такого перемещения, вызванного переброской только одного электрона из валентной зоны в зону проводимости.

Описание движения электронов, находящихся в валентной зоне, является весьма сложным. Для того чтобы избежать трудностей, возникающих при этом описании, было введено понятие квазичастицы, получившей название дырки. Заряд дырки положителен и по величине равен абсолютному заряду электрона 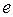, а в электрическом поле она движется в направлении, противоположном движению электрона. Таким образом, в валентной зоне перемещение электронов заменяется перемещением положительно заряженных дырок в противоположном направлении (рис. 13, б).

Валентную зону с небольшим числом вакантных мест у потолка зоны можно представить как пустую зону с соответствующим числом дырок в месте расположения вакансий (рис. 13, в). Следует подчеркнуть, что понятие дырки введено только для удобства описания движения всей многоэлектронной системы в полупроводнике. Проводимость, обусловленная дырками, появившимися в валентной зоне, называется дырочной.

При отсутствии в полупроводнике внешнего электрического поля электроны проводимости и дырки движутся хаотически. При появлении в полупроводниковом кристалле внешнего поля на хаотическое движение электронов и дырок накладывается их упорядоченное движение. При этом электроны движутся против поля, а дырки – в направлении поля. Следовательно,собственная электропроводность полупроводника обусловлена носителями тока двух типов: отрицательными электронами и положительными дырками.

Как зависит концентрация электронов 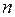, расположенных в зоне проводимости полупроводника, от температуры? Воспользуемся функцией распределения электронов Ферми-Дирака (7)

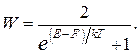(8)

В квантовой теории доказывается, что уровень Ферми 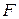в собственном полупроводнике лежит посередине запрещенной зоны шириной 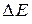. Электроны зоны проводимости, имеющие энергию 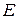, располагаются на «хвосте» кривой распределения Ферми-Дирака (рис. 14).

Для этих электронов выполняется приближенное равенство

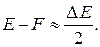(9)

С учетом (9) выражение (8) принимает вид

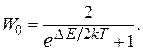(10)

На величину 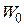в формуле (10) следует смотреть как на среднее число электронов, расположенных на энергетических уровнях зоны проводимости.

Численные оценки показывают, что даже при достаточно высокой для полупроводников температуре 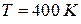величина энергии теплового движения остается сравнительно небольшой: 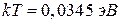. Следовательно, для собственного полупроводника с шириной запрещенной зоны 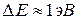в широком интервале температур будет выполняться неравенство

.

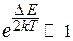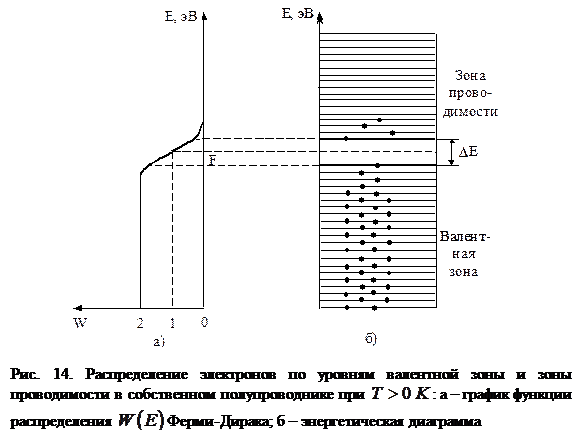Тогда выражение (10) можно упростить:

.

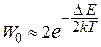(11)

Так как концентрация электронов 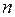, находящихся в зоне проводимости, пропорциональна среднему числу электронов 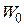на уровнях в этой зоне, то на основании (11) можно записать следующее выражение для зависимости концентрации n от температуры :

,

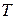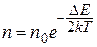(12)

где .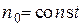

Как уже указывалось ранее, носителями тока в полупроводнике являются электроны и дырки (рис. 13, в). Концентрация дырок, появившихся в валентной зоне, равна концентрации электронов 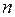, перешедших в зону проводимости из валентной зоны. С учетом этого формула (2), записанная для удельной электропроводности 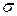собственного полупроводника, примет следующий вид:

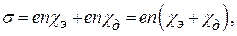(13)

где 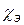– подвижность электронов; 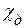– подвижность дырок.

В формуле (13) с ростом температуры 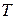концентрация носителей тока 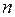резко возрастает по закону, близкому к показательному (12), а подвижность электронов 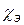и дырок 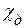слабо уменьшается, так же как подвижность электронов в металле. Поэтому для упрощения выражения (13) слабой температурной зависимостью подвижносте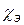й и 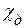можно пренебречь и считать сумму 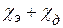величиной неизменной. Тогда с учетом (12) формулу (13) можно записать следующим образом:

,

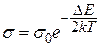(14)

где .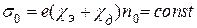

Учитывая, что удельное сопротивление полупроводника 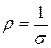, на основании (14) получаем формулу для зависимости 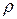от температуры :

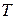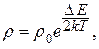(15)

где .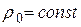

Электрическое сопротивление 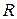полупроводникового образца зависит от его геометрических размеров и удельного сопротивления полупроводника 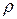. Геометрические размеры мало зависят от температуры, поэтому зависимость 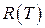определяется формулой

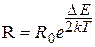, (16)

где .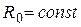

График этой зависимости изображен на рис. 15, а.

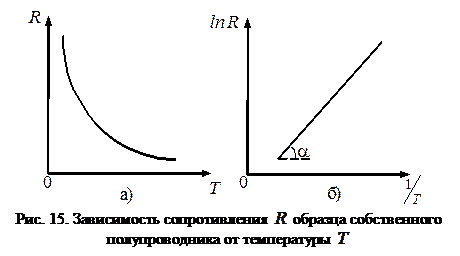Прологарифмировав выражение (16), можно получить более удобную для расчетов линейную зависимость логарифма сопротивления полупроводника 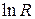от величины, обратной температуре :

.

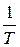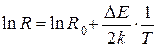(17)

График этой зависимости представлен на рис. 15, б. Линейная функция (17) позволяет относительно просто определить ширину запрещенной зоны 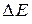собственного полупроводника по тангенсу угла наклона 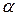графика экспериментальной зависимости 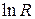от 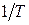(рис. 15, б):