Опыт 2 . Наблюдение дифракции света на дифракционной решетке. Определение периодов двумерной структуры

Принадлежности: лазер, двумерная дифракционная решетка, экран.

Простая дифракционная решетка представляет собой стеклянную пластинку, на которой нанесен ряд параллельных штри­хов. Места, где прочерчены штрихи, являются практически неп­розрачными промежутками между неповрежденными частями пластинки (которые являются щелями). Таким образом, дифракционная решетка представляет собой периодическую систему щелей. Щели следуют друг от друга на определенном расстоянии d, которое называется периодом или постоянной решетки. Период d равен

d =а+b,

где а - ширина штриха, и b- ширина щели.

Поставим две дифракционные решетки одну за другой так, чтобы их штрихи были взаимно перпендикулярны. Первая решетка (штрихи которой, скажем, вертикальны) даст в горизонтальном направлении ряд максимумов освещенности, положения которых определяются условием:

d_1*sinφ₁=+m₁ λ , m₁₌0,1,2,… (3)

где m₁- порядок максимума,

φ₁ - угол m - го дифракционного максимума,

λ - длина волны света,

d₁ - период первой решетки.

Вторая решетка с горизонтальными штрихами даст максимумы в вертикальном направлении, положение которых определится условием

d_2*sinφ₂=+m₂λ, m₂₌0,1,2,… (4)

В итоге дифракционная картина будет иметь вид правильно расположенных пятен, каждому из которых соответствует два целочисленных индекса m₁ и m₂

(рис. 8),

m₁ ; m₂

0, 2

• • • • • • •

0, 1

• • • • • • •

-0,3

-0,2

-0,1

0; 0

3,0

2,0

1,0

• • • • • • • m₁ ; m₂

0; -1

• • • • • • •

0; -2

• • • • • • •

Рис.8

Еcли штрихи решеток не перпендикулярны, а составляют некоторый угол 0<a <90 , то положение максимумов (светлых пя­тен) изменится. Следовательно, по расположению пятен можно судить о структуре штрихов в пространстве, т.е. о значении периодов d₁ и d₂, и взаимной ориентации решеток.

В том случае, когда структура препятствий не периодична, дифракционная

картина получится более сложной. В частности, если в пространстве беспорядочно располагаются непрозрачные частицы близкие по размерам и форме (запыленная пластина, морозные узоры на стекле), то образованная ими структура эквивалентна совокупности простых решеток всех возможных направлений, а дифракционнаякартина будет в виде чередую­щихся светлых и темных концентрических кругов.

Для определения периодов двумерной решетки d₁ и d₂ соби­рают установку по рис.9, где 1 - решетка, 2 - экран. Из рисунка видно, что

tg φ_m=x_m/2l

1 2

х_m

Луч лазера

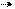
Рис. 9

Из соотношений (3) и (4) получаем

d₁ = ± m₁ λ/ sin [arctg (x_m1 / 2 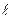)] (5)

d₂ = ± m₂ λ / sin [arctg (x_m2 / 2 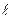)] (6)

Задание: l. На миллиметровой бумаге на экране отметьте

положение дифракционных максимумов.

2. Используя формулы (5) и (6), рассчитайте периоды двумерной

решетки d₁ и d₂.

Опыт 3. Наблюдение линейной поляризации лазерного излу­чения.

Принадлежности: лазер, поляризатор, экран.

Излучение лазера является линейнополяризованным. В этом можно убедиться, пропуская лазерное излучение через поляризатор. При его вращении относительно луча лазера как оси интенсивность света через 90^o меняется от максимальной практи­чески до нуля согласно закону Малюса. Если бы луч лазера неполяризованным, то интенсивность луча при вращении поляри­затора не менялась бы.