Приложение Д – Примеры построения диаграммы Найквиста

Пример Д1. Построить АФЧХ импульсной разомкнутой системы, если передаточная функция непрерывной части 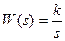; передаточная функция экстраполятора нулевого порядка .

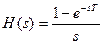Решение

1 Передаточная функция в z-форме (см. пример В1)

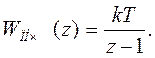(В1.1)

2 Заменяя в (В1.1) z на 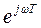, получим комплексный коэффициент передачи

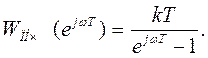(В1.2)

3 Используя формулу Эйлера, запишем (В1.2) в виде

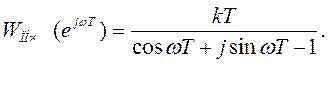(В1.3)

4 Выделим вещественную и мнимую части выражения (В1.3)

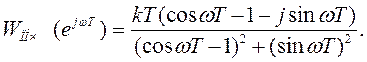
Преобразуем последнее выражение

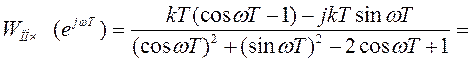
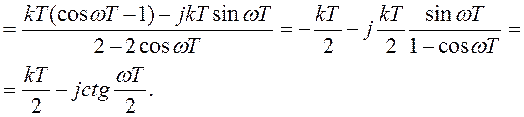
Вещественная часть Р^*(ω)=- kT/2;

мнимая часть .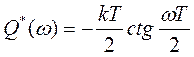

Вещественная часть не зависит от частоты, мнимая часть при изменении частоты от ω=0 до ω=π/Т изменяется от -∞ до нуля.

5 АФЧХ приведена на рисунке Д1

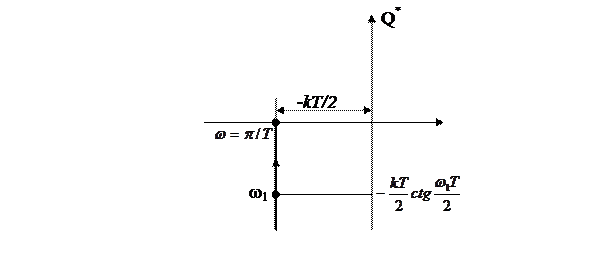
Рисунок Д1 – Амплитудно-фазовая частотная характеристика импульсной системы с непрерывной частью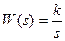

Пример Д2.Передаточная функция непрерывной части (рисунок В1) 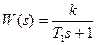; передаточная функция экстраполятора нулевого порядка .

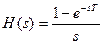Решение

1 Передаточная функция в z-форме (см. пример В2)

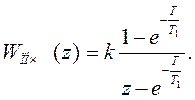
2 Заменив z=e^jωT и применяя формулу Эйлера ( 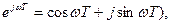получим

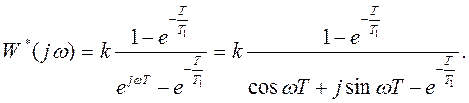
3 Выделяем вещественную и мнимую части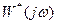

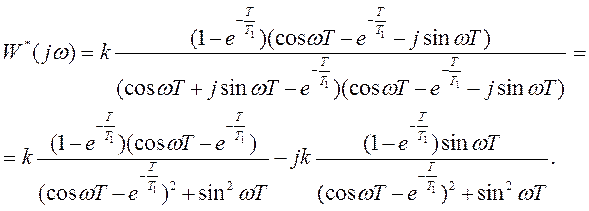
Вещественная часть

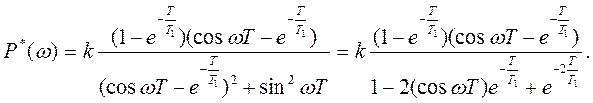
Мнимая часть

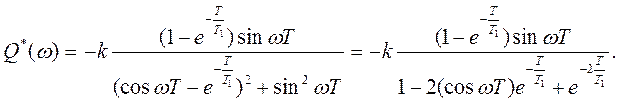
4 АФЧХ для рассматриваемого случая приведена на рисунке Д2. Она представляет собой полуокружность, центр которой лежит на вещественной оси на расстоянии С от начала координат с радиусом R.

; ;

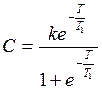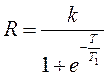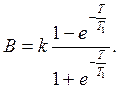
При ω=0 .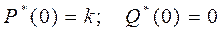

При ω=π/Т

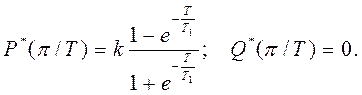
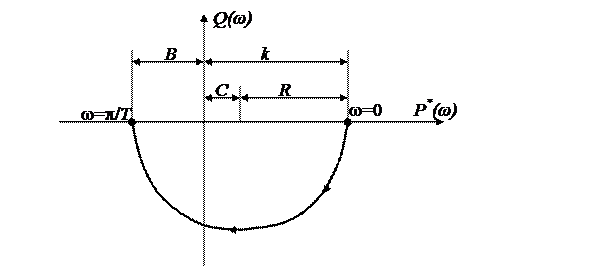
Рисунок Д2 – Амплитудно-фазовая частотная характеристика импульсной системы с апериодическим звеном

Приложение Е – Построение логарифмических частотных характеристик импульсной разомкнутой системы

Пример Е1. Для условий примера Д1 построить логарифмические частотные характеристики.

Решение

1 Передаточная функция в z-форме

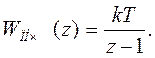(Е1.1)

2 Подстановкой в (Е1.1) 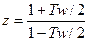, получим передаточная функция W(w)

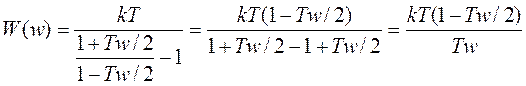. (Е1.2)

3 Частотная передаточная функция

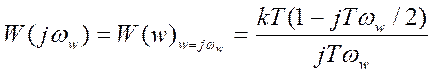. (Е1.3)

4 Построение ЛАЧХ

Согласно (Е1.3) ЛАЧХ состоит из 2-х асимптот, сопрягающихся на частоте ω_w=2/Т.

Уравнение первой асимптоты

,

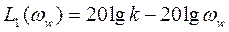что соответствует прямой с наклоном -20 дБ/дек, проходящей через точку с координатами .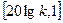

Уравнение второй асимптоты

,

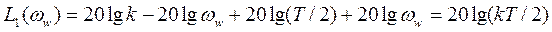что соответствует прямой, параллельной оси абсцисс.

5 Построение фазовой частотной характеристики (ФЧХ)

Согласно (Е1.3) .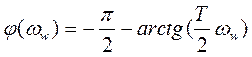

Логарифмические частотные характеристики приведены на рисунке Е1

Рисунок Е1 – Логарифмические частотные характеристики импульсной системы с интегратором в непрерывной части

Как видно из рисунка, в области низких частот 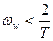частотные характеристики импульсной системы достаточно близки частотным характеристикам ее непрерывной части: с увеличением частоты в 10 раз амплитуда уменьшается на 20 децибел, фаза близка к π/2 . Однако, на высоких частотах 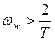логарифмические характеристики ИС значительно отличаются от характеристик непрерывной части. Фильтрующие свойства интегратора практически не проявляются.

Пример Е2. Построить логарифмические частотные характеристики импульсной системы, если непрерывная часть представляет апериодическое звено первого порядка с апериодическим звеном, а формирующий элемент – экстраполятор нулевого порядка (рисунок В1). Передаточная функция импульсной системы в этом случае рассмотрена в примере В2 и имеет вид

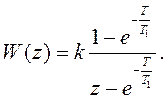
Решение

1) Передаточная функция W(w)

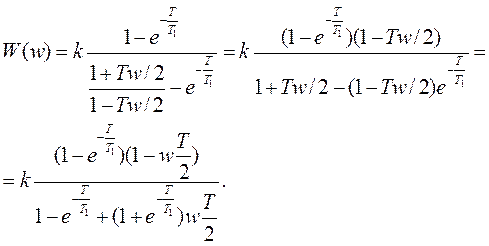
2) Частотная передаточная функция

,

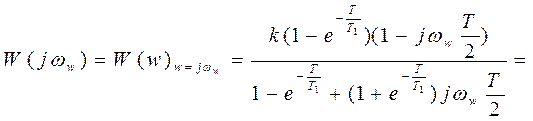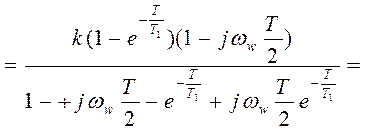
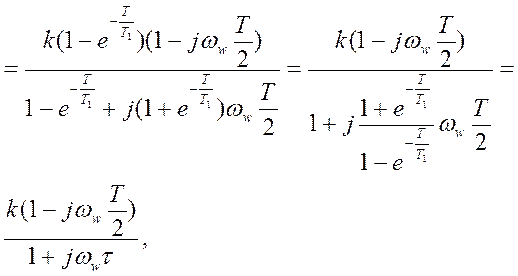
где принято 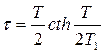( 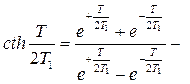гиперболический котангенс).

3) Если период квантования Т<2T₁, то 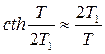и, следовательно, .

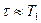Комплексный коэффициент передачи в этом случае равен

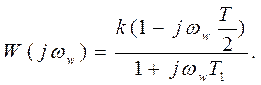
4) Если период квантования Т>2T1, то 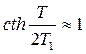и, следовательно,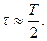

Комплексный коэффициент передачи в этом случае равен

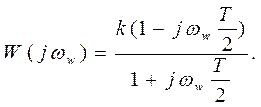
5) ЛАЧХ для случая Т<2T₁, т.е. период квантования меньше удвоенной постоянной времени звена, определятся выражением

.

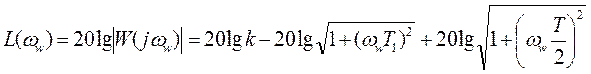Асимптотическая ЛАЧХ состоит из трех асимптот с частотами сопряжения 1/Т₁ и 2/Т.

Уравнение первой асимптоты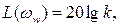

Уравнение второй асимптоты ,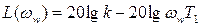

Уравнение третьей асимптоты .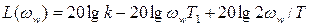

6 ЛФЧХ для рассматриваемого случая

.

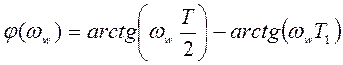7 Логарифмические частотные характеристики приведены на рисунке Е1

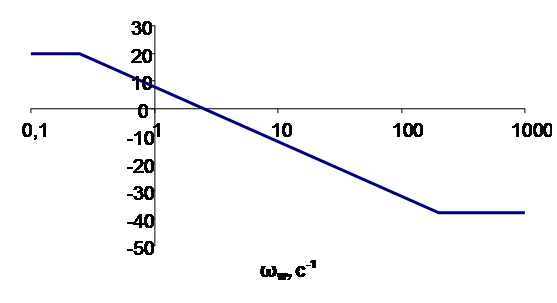
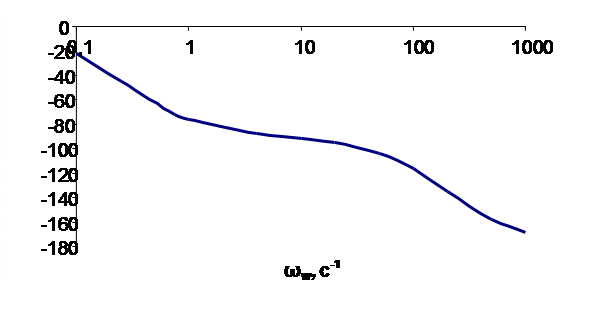
Рисунок Е1 – Логарифмические частотные характеристики импульсной системы с апериодическим звеном в непрерывной части при Т<2T₁

Из рисунка Е1 можно сделать вывод, что на частотах, меньших 2/Т, частотные характеристики ИС совпадают с частотными характеристиками ее непрерывной части. В области высоких частот, как и в случае с интегрирующим звеном, фильтрующие свойства апериодического звена почти не проявляются.

Библиографический список

1 Теория автоматического управления: Учеб. для вузов/ С.Е.Душин, Н.С.Зотов и др.; под ред. В.Б.Яковлева. – М: Высш. шк., 2003. – 567 с.: ил.

2 Ким, Д.П. Теория автоматического управления. Т.1Линейные системы. – М.:ФИЗМАТЛИТ, 2003. – 288 с.

3 Певзнер, Л.Д. Практикум по теории автоматического управления: Учеб. пособие / Л.Д.Певзнер. – М.:Высш. шк., 2006. – 590 с.: ил.

4 Ким Д.П., Дмитриева Н.Д. Сборник задач по теории автоматического управления. Линейные системы. – М.: ФИЗМАТЛИТ, 2007. – 168 С.
5 Филипс Ч., Харбор Р. Системы управления с обратной связью. – М.: Лаборатория Базовых Знаний, 2001. – 616 с.
6 Пантелеев, А.В. Теория управления в примерах и задачах: Учеб. пособие/ А.В.Пантелеев, А.С.Бортаковский. – М.: Высш. шк., 2003. - 583 с.