Дифракция Фраунгофера на одной щели

Пусть на бесконечно длинную щель шириной a падает нормально плоскости щели плоская монохроматическая световая волна. Поместим за щелью собирающую линзу, а в фокальной плоскости линзы – экран. Положение точки экрана P, где соберутся вторичные волны, определяется углом дифракции φ. Оптическая разность хода между крайними лучами MC и AD, идущими в направлении угла φ , равна AB:

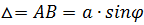
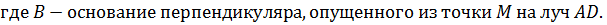
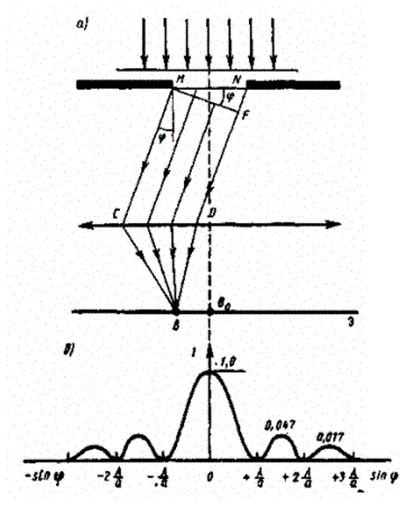Разобьем открытую часть волновой поверхности в плоскости щели MA на зоны Френеля, имеющие вид полос, параллельных ребру M щели. Ширина каждой зоны выбирается так, чтобы разность хода от краев этих зон была равна . Все точки волнового фронта в плоскости щели будут колебаться в одинаковой фазе. Амплитуды вторичных волн в плоскости щели будут равны, так как выбранные зоны Френеля имеют одинаковые площади и одинаково наклонены к направлению наблюдения. Число зон Френеля, укладывающихся на ширине щели, зависит от угла φ. При интерференции света от каждой пары соседних зон Френеля амплитуда результирующих колебаний равна нулю, так как колебания от каждой пары соседних зон взаимно гасят друг друга.

Следовательно, если число зон Френеля чётное, то:

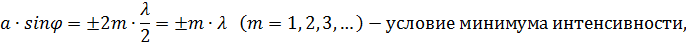
и в точке P и наблюдается дифракционный минимум(полная темнота),

если число зон Френеля нечётное, то:

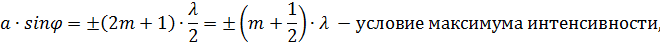
и наблюдается дифракционный максимум. Отметим, что в направлении 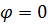щель действует как одна зона Френеля, и в этом направлении свет распространяется с наибольшей интенсивностью, т. е. в точке O наблюдается центральный дифракционный максимум.

Распределение интенсивности на экране, получаемое вследствие дифракции (дифракционный спектр) приведено на рис.б. Расчеты показывают, что интенсивности в центральном и последующих максимумах относятся как 1 : 0,047 : 0,017 : 0,0083 : ..., т. е. основная часть световой энергии сосредоточена в центральном максимуме.

2)Дифракция Фраунгофера на дифракционной решётке.

Одномерная дифракционная решетка- система параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками (штрихами). Дифракционная картина на решетке определяется как результат взаимной интерференции волн, идущих от всех щелей, т. е. в дифракционной решетке осуществляется многолучевая интерференция когерентных дифрагированных пучков света, идущих от всех щелей.

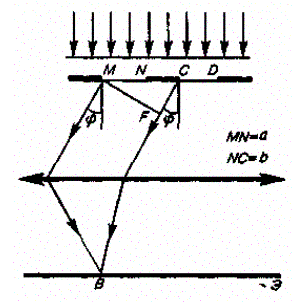
Рассмотрим дифракционную решетку. Расположим параллельно решётке собирательную линзу, в фокальной плоскости которой поставим экран. Пусть плоская монохроматическая волна падает нормально к плоскости решетки.

Если ширина каждой щели равна a, а ширина непрозрачных участков между щелями b , то величина d называется постоянной (периодом) дифракционной решётки.

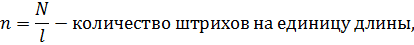
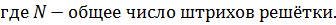
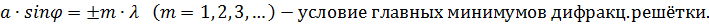
Так как щели находятся друг от друга на одинаковых расстояниях, то разности хода лучей, идущих от двух соседних щелей, будут для данного направления φ одинаковы в пределах всей дифракционной решетки и равны:

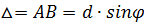
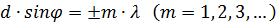
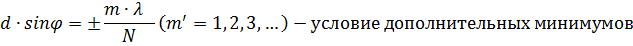
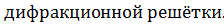
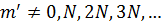
Чем больше щелей N, тем большее количество световой энергии пройдет через решетку, тем больше минимумов образуется между соседними главными максимумами, тем, следовательно, более интенсивными и более острыми будут максимумы.

В точке O всегда наблюдается центральный дифракционный максимум.

Дифракционная решётка как спектральный прибор.

Дифракционную решётку применяют в спектральных приборах.

Основными характеристиками всякого спектрального прибора являются его дисперсия и разрешающая способность. Дисперсия определяет угловое или линейное расстояние между двумя спектральными линиями, отличающимися по длине волны на единицу. Разрешающая способность определяет минимальную разность длин волн δλ , при которой две линии воспринимаются в спектре отдельно.

Угловой дисперсией называется величина

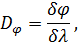
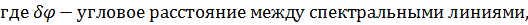
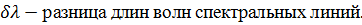
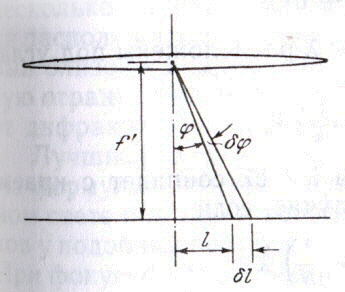
Чтобы найти угловую дисперсию дифракционной решётки, продифференцируем условие главного максимума слева по φ , а справа по λ :

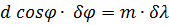
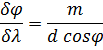
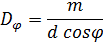
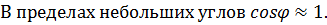
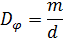
Линейной дисперсией называется величина

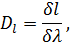
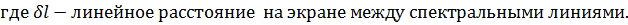
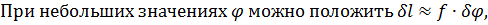
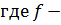фокусное расстояние линзы.

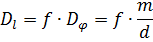
Разрешающей способностью спектрального прибора принято называть безразмерную величину:

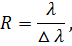
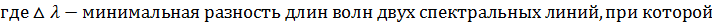
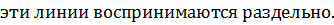
В качестве критерия разрешения используется обычно критерий разрешения Рэлея.

Спектральные линии считаются разрешёнными, если главный максимум дифракционной картины для одной спектральной линии совпадает по своему положению с первым дифракционным минимумом для другой спектральной линии.

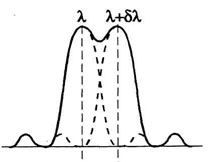
Разрешающая способность дифракционной решётки:

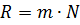
Поляризация света. Виды поляризованного света. Степень поляризации. Закон Малюса. Закон Брюстера. Двойное лучепреломление. Искусственная анизотропия. Вращение плоскости поляризации.

Поляризация – это ориентированность колебаний световой волны в пространстве. Эти колебания перпендикулярны направлению движения луча света. Электромагнитная волна является поперечной. Колебания вектора напряженности электрического поля и вектора индукции магнитного поля в электромагнитной волне происходят в перпендикулярных к направлению распространения волны плоскостях. Направление вектора напряженности 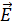электрического поля определяет тип поляризации световой волны.

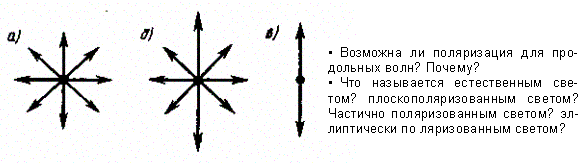
Свет со всевозможными равновероятными ориентациями светового вектора – вектора напряженности 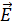электрического поля называется естественнымилинеполяризованным (рис. а; луч перпендикулярен плоскости рисунка). В результирующей волне вектор 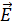беспорядочно изменяет свою ориентацию во времени, так что в среднем все направления колебаний оказываются равноправными.

Свет, в котором направления колебаний светового вектора каким-то образом упорядочены, называется поляризованным.

Свет может оказаться поляризованным при отражении или рассеянии. В частности, голубой свет от неба частично или полностью поляризован. Однако, свет, испускаемый обычными источниками (солнечный свет, излучение ламп накаливания) неполяризован.

Свет, в котором колебания светового вектора одного направления преобладают над колебаниями других направлений, называется частично поляризованным(рис. б).

Свет, в котором вектор Е колеблется только в одном направлении, перпендикулярном лучу (рис. в), называется плоскополяризованным (линейно поляризованным). Линейно поляризованный свет испускается лазерными источниками.

Плоскость, проходящая через направление колебаний светового вектора плоскополяризованной волны и направление распространения этой волны, называется плоскостью поляризации.

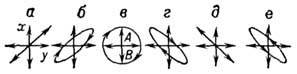
Плоскополяризованный свет является предельным случаем эллиптически поляризованного света- света, для которого вектор изменяется со временем так, что его конец описывает эллипс, лежащий в плоскости, перпендикулярной лучу (рис. б, г, е). Если эллипс поляризации вырождается в прямую (при разности фаз φ , равной нулю или π), то имеем дело с рассмотренным выше плоскополяризованным светом (рис. а, д), если в окружность и равенстве амплитуд складываемых волн), то имеем дело с циркулярно поляризованным (поляризованным по кругу) светом(рис. в).

В зависимости от направления вращения вектора различают правую и левую эллиптическую и круговую поляризацию. Если по отношению к направлению, противоположному направлению луча, вектор 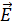вращается по часовой стрелке, поляризация называется правой, в противном случае – левой.

Естественный свет можно преобразовать в плоскополяризованный, используя так называемые поляризаторы,пропускающие колебания только определенного направления (например, пропускающие колебания, параллельные главной плоскости поляризатора, и полностью задерживающие колебания, перпендикулярные этой плоскости).

Если пропустить частично поляризованный свет через поляризатор, то при вращении прибора вокруг направления луча интенсивность прошедшего света будет изменяться в пределах 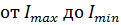при повороте на угол, равный .

Степенью поляризацииназывается величина:

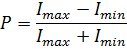
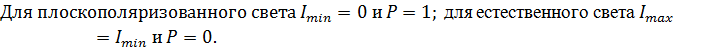
К эллиптически поляризованному свету понятие степени поляризации не применимо (у такого света колебания полностью упорядочены).

Закон Малюса.

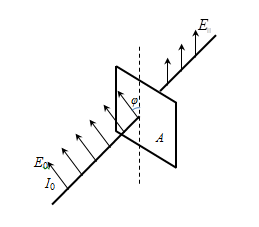
Поляризованный свет можно получить из естественного с помощью поляризаторов – анизотропных кристаллов, пропускающих свет только в одном направлении (исландский шпат, кварц, турмалин). Поляризатор, анализирующий в какой плоскости поляризован свет, называетсяанализатором. Поляризатор по своей конструкции ничем не отличается от анализатора. Разница в функциях: поляризатор выделяет из естественного света пучок с одним направлением колебаний вектора 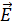, а анализатор определяет, каково направление этих колебаний. Именно поэтому поляризаторы и анализаторы носят общее название поляроиды.

Если на анализатор падает плоско поляризованный свет амплитудой 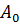и интенсивности 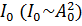, плоскость поляризации которого составляет угол φ с плоскостью анализатора, то падающее электромагнитное колебание можно разложить на два колебания; с амплитудами 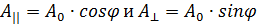, параллельное и перпендикулярное плоскости анализатора. Сквозь анализатор пройдет составляющая параллельная плоскости анализатора, то есть составляющая 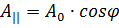, а перпендикулярная составлявшая будет задержана анализатором. Тогда интенсивность прошедшего через анализатор света будет равна:

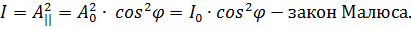
Закон Малюса: Интенсивность света, прошедшего через поляризатор, прямо пропорциональна произведению интенсивности падающего плоско поляризованного света 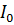и квадрату косинуса угла между плоскостью падающего света и плоскостью поляризатора.

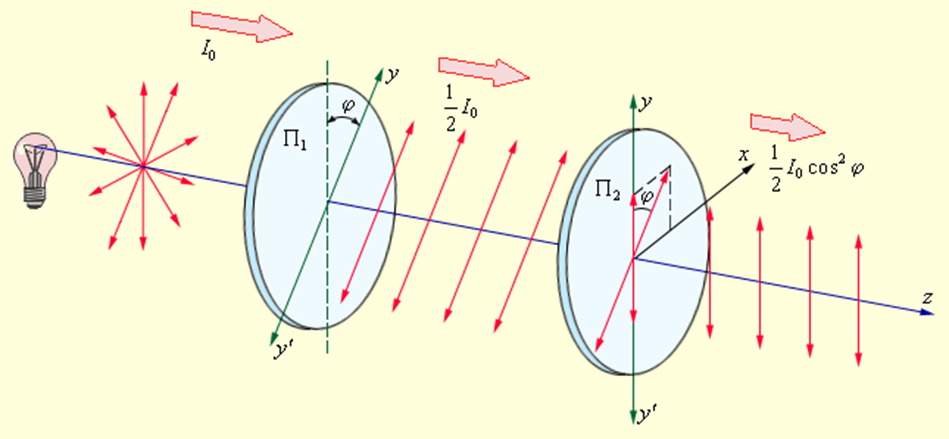
Поставим на пути естественного луча два поляризатора , плоскости которых образуют угол φ. Из первого поляризатора выйдет плоскополяризованный свет, интенсивность которого составит половину естественного:

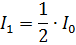
Согласно закону Малюса из второго поляризатора выйдет свет интенсивности, равной:

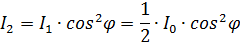
Закон Брюстера.

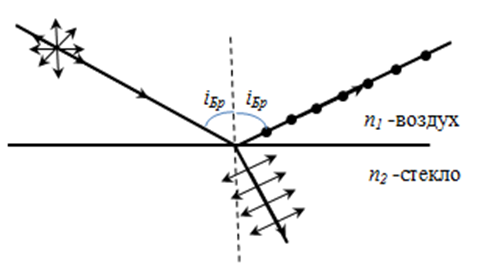
При угле падения, равном углу Брюстера :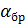

1. отраженный от границы раздела двух диэлектриков луч будет полностью поляризован в плоскости, перпендикулярной плоскости падения;

2. степень поляризации преломленного луча достигает максимального значения меньшего единицы;

3. преломленный луч будет поляризован частично в плоскости падения;

4. угол между отраженным и преломленным лучами будет равен 90°;

5. тангенс угла Брюстера равен относительному показателю преломления:

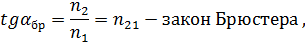
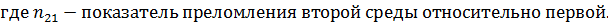
Угол падения(отражения) – угол между падающим (отраженным) лучом и нормалью к поверхности.

Плоскость падения – плоскость, проходящая через падающий луч и нормаль к поверхности.

Двойное лучепреломление.

Все кристаллы, кроме кристаллов кубической системы – изотропных кристаллов, являются анизотропными, то есть свойства кристаллов зависят от направления. Все прозрачные анизотропные кристаллы способны раздваивать проходящий через них световой луч на два луча, распространяющиеся с разными скоростями и в различных направлениях. Это явление получило название двойное лучепреломление.

Анизотропные кристаллы подразделяются на одноосные и двуосные. У одноосных кристаллов имеются одно направление, вдоль которого световой луч идёт, не раздваиваясь, называемое оптической осью кристалла. Плоскость, проходящая через световой луч и оптическую ось, называется главным сечением кристалла. У двуосных кристаллов имеется два направления, вдоль которых не происходит двойного лучепреломления.

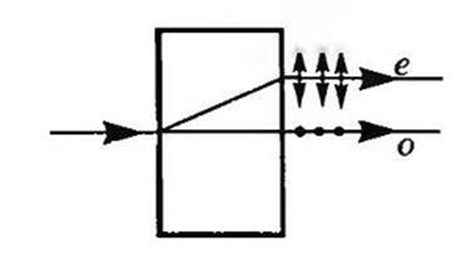
У одноосных кристаллов (исландский шпат, кварц, турмалин) один из преломленных лучей подчиняется обычному закону преломления:

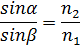
Он лежит в одной плоскости с падающим лучом и нормалью к преломляющей поверхности. Этот луч называется обыкновенным и обозначается буквой о. В обыкновенном луче колебание светового вектора перпендикулярно главному сечению кристалла.

Для другого луча, называемого необыкновенным (его обозначают буквой e), отношение синусов угла падения и угла преломления не остаётся постоянным при изменении угла падения. Он не лежит в одной плоскости с падающим лучом и нормалью к преломляющей поверхности. В необыкновенном луче колебание светового вектора параллельно главному сечению кристалла.

У двуосных кристаллов (слюда, гипс) оба луча необыкновенные.

Понятие обыкновенного и необыкновенного лучей имеет место, пока эти лучи распространяются в кристалле, при выходе из кристалла эти понятия теряют смысл, то есть лучи отличаются только плоскостями поляризаций.

Природа двойного лучепреломления связана с тем, что обыкновенные и необыкновенные лучи имеют разные скорости :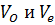

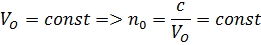
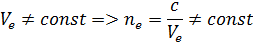
Таким образом, один из лучей (обыкновенный) имеет для всех направлений одно и то же значение показателя преломления, для другого луча (необыкновенного) показатель преломления зависит от направления луча.

А так как 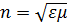, то можно сказать, что первопричиной двойного лучепреломления является анизотропия (зависимость от направления) диэлектрической проницаемости кристалла.

Кристаллы, у которых 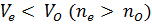называются положительными, а у которых 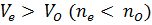называются отрицательными.

После выхода из пластинки обыкновенный и необыкновенный лучи, складываясь, дают в общем случае свет эллиптической поляризации. Ориентация осей эллипса и соотношение между ними будут зависеть от поляризации падающего на пластинку света, толщины и ориентации пластинки.

Рассмотрим частный случай.

Толщина пластинки такова, что разность хода двух волн составляет четверть волны:

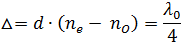
Такая пластинка называется пластинкой в четверть длины волны.

Плоскополяризованный свет, проходящий через данную пластинку, становится эллиптически поляризованным и наоборот.

Чтобы наблюдать интерференцию обыкновенного и необыкновенного лучей, пластинку помещают между скрещивающимися поляризаторами.