Методические указания по физике к контрольному заданию № 1

3.1 Контрольное задание № 1 относится к разделам курса физики «Механика», «Молекулярная физика» и «Термодинамика».

3.2 Раздел физики «Механика» является базой для изучения таких общеинженерных дисциплин, как «Теоретическая механика», «Сопротивление материалов», «Детали машин», а также целого ряда специальных: «Автомобильная техника», «Двигатели» и т. д.

3.3 В задачах кинематики бывает нужным использовать аппарат дифференциального и интегрального исчислений, чтобы определять мгновенные скорость и ускорение по заданной зависимости координаты от времени, а также решать обратные задачи.

Пример 1. Определить скорость и ускорение автомобиля, движущегося согласно уравнению S = At + Bt² + Ct³, через 5 с после начала движения. Коэффициенты: А = 2 м/с; В = 2 м/с² и С = 0,1 м/с³.

Дано: Решение

S = At + Bt² + Ct³ Если закон движения задается в виде S = f(t), то

t = 5 c полезно уяснить некоторые положения.

A = 2 м/с 1) Когда вместо координаты x можно использовать

B = 2 м/c² путь S? Если движение прямолинейное без смены

С = 0,1 м/с³ направления, то .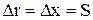

υ - ?; a - ? 2) Что можно сказать по виду уравнения о движении?

При равномерном движении x = x₀ + υ·t;

При равноускоренном движении x = x₀ + υ₀t + .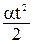

3) Что в заданном по условию уравнении означают коэффициенты при t?

υ₀ = A – начальная скорость;

a₀ = 2B – начальное ускорение.

Значения x₀, υ₀, a₀ можно получить, подставив t = 0 в уравнения

х = f (t), х′ = f (t), х″ = f (t).

4) Чему равны скорость и ускорение в момент времени t = 5 c ?

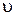= x′ = A + 2Bt + 3Ct² , a = 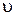′ = 2B + 6Ct.

Подставив данные, получим:

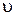= 29,5 м/с, a = 7 м/с².

Ответ: 29,5 м/с; 7 м/c² .

Пример 2. Движение тела определяется уравнением х = 3 + 4t - t², м. Найти путь, пройденный за 4 с. Возникнет ли смена направления движения?

Для решения такой задачи нужно найти момент времени, когда скорость обращается в нуль, определить перемещения при разных направлениях движения и их модули сложить:

S = ∑|∆r_і|.

Определим, когда скорость движения обращается в нуль:

х′ = 4 – 2t = 0, t = 2 с.

Отсюда следует, что через 2 с после начала движения тело начнет двигаться в противоположную сторону. Тогда

S = |Δr₁| + |Δr₂|,

где Δr₁ – перемещение за время от t = 0 до t = 2 с;

Δr₂ – перемещение за время от t = 2 с до t = 4 с.

Для обоих случаев

Δr = x₂ – x₁ = 3 + 4t₂ – t 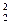– (3 + 4t₁ – t ) = 4 (t₂ – t₁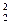) – (t – t ) =

= [4 – ( t₂ + t₁)] · ( t₂ – t₁),

Отсюда Δr₁ = [4 – (2 + 0)] · (2 –0) = 4,

Δr₂ = [4 – (4 + 2)] · (4 – 2) = –4,

Δr = Δr₁ + Δr₂ = 4 – 4 = 0.

Отсюда следует, что за 4 с тело вернулось в точку с координатой х = х₀ = 3 м.

S = 4 + |–4| = 8.

Ответ: 8 м; смена направления движения возникает при t = 2 с.

В ряде случаев при решении задач кинематики нужно уметь представить сложное движение как сумму простых, каждое из которых подчиняется собственной закономерности.

Пример 3. В противоположных точках основания сопки длиной 1500 м находятся миномет и цель. Под каким углом к горизонту следует установить ствол миномета, чтобы «накрыть» цель? Скорость вылета мины 300 м/с. Высота сопки 800 м.

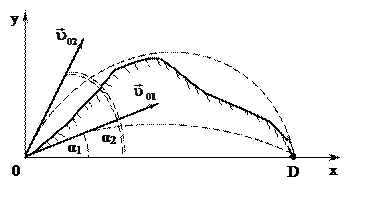Дано: Решение

ОD = 1500 м

υ₀ = 300 м/с

h = 800 м

α - ?

Движение мины можно представить как результат сложения ее движения по оси х с постоянной скоростью 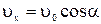, и по оси у со скоростью 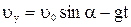(равнозамедленное движение).

Очевидно, О 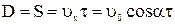, где t = время полета мины. Оно равно удвоенному времени подъема мины 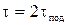до высшей точки траектории.

В этой точке υ_y = 0, следовательно 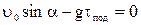, то есть

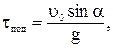
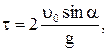
откуда 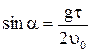. Поскольку 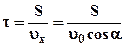, получим ,

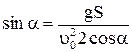то есть 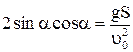. Таким образом, .

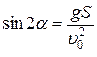Это уравнение допускает два разумных физических решения:

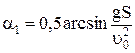и .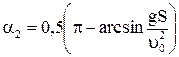

Первое решение дает ,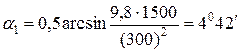

а второе: 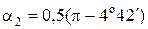= 85^o18΄.

Для выбора решения, определим высоту подъема мины. Исходя из формулы 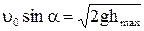, получим

,

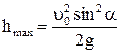откуда 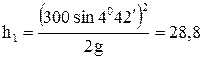м,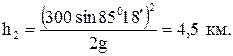

Сопоставляя эти результаты с высотой сопки, получим, что первый угол слишком мал (мина «врежется» в сопку), а мина, выпущенная под углом a₂, «накроет» цель.

Ответ: 85^о18΄.

3.4 При решении задач динамики следует, как правило, опираться на второй закон Ньютона в векторной форме.Схема решения таких задач часто выглядит следующим образом:

- записать условие задачи, в том числе в компактном виде;

- сделать эскиз;

- расставить векторы сил, действующих на рассматриваемые тела;

- записать используемый закон применительно к данным условиям в векторной форме;

- выбрать значимые для данной задачи направления (оси координат);

- спроецировать уравнение на выбранные направления, получив уравнение (уравнения) в скалярной форме;

- решив скалярные уравнения, найти искомые величины;

- проанализировать полученный результат.

Пример 4. Тело скользит по наклонной плоскости, составляющей с горизонтом угол 30 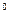. Зависимость пройденного телом пути от времени задана уравнением S = At + 3Bt 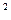, где B = 0,42 м/c². Найти коэффициент трения тела о плоскость.

Дано: Решение

a = 30⁰

S = At + 3B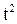

B = 0,42 м/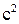

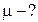
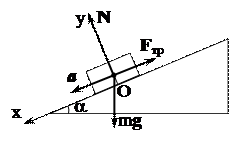
Второй закон Ньютона для данной задачи m .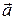

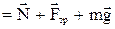На OX: ma = mgsin – .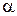

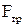На OY: O = mgcos 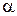– N.

Так как 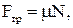а N = mg cos 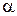, то ma = mgsin 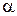– 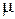mgcos 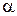. Из уравнения движения a = 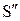= 6В. Подставив это значение и выразив коэффициент трения,

; .

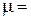
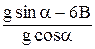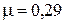Ответ: .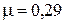

3.5 При решении ряда задач динамики следует пользоваться таким мощным средством, как законы сохранения энергии и импульса. Для этого, прежде всего, нужно определить, какие именно тела следует в данной задаче включать в систему тел, а какие считать внешними по отношению к этой системе. Здесь имеется свобода выбора, которой нужно грамотно пользоваться, чтобы облегчить решение задачи.

Законы сохранения позволяют решать многие задачи очень простыми средствами, однако следует постоянно иметь в виду, что они выполняются только при определенных условиях, наличие которых нужно оценить. В частности, нужно определить, можно ли рассматриваемую систему тел считать замкнутой, а действующие в ней силы консервативными.

Пример 5. Танк массой 25 т, двигаясь со скоростью 54 км/ч, производит выстрел под углом 30⁰ к направлению движения. Масса снаряда 10 кг, его начальная скорость 800 м/с, продолжительность выстрела 3·10^-3 с. На сколько изменится скорость танка непосредственно после выстрела? Какую силу толчка испытывает при выстреле водитель танка массой 80 кг?

Дано: СИ Решение

m₁ = 25 т 25·10³ кг

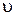₁ = 54 км/ч 15 м/c

a = 30^o

m₂ = 10 кг

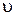₂ = 800 м/с

Dt = 3·10^-3 с

m₃ = 80 кг

D 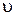- ? F - ?

Условие задачи позволяет считать систему тел «танк-снаряд» замкнутой.

Изменение скорости танка после выстрела

,

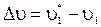где 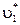– скорость танка непосредственно после выстрела.

Используя закон сохранения импульса, определим :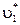

.

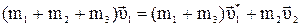Проецируя это уравнение на ось х, получим

.

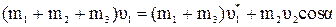Отсюда

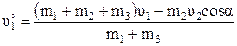
Изменение скорости танка

.

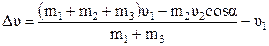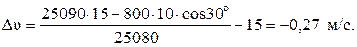
Знак «минус» показывает, что скорость танка стала меньше. Вернемся к рисунку и убедимся, что изобразили верно.

Силу толчка найдем, используя второй закон Ньютона: .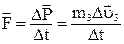

Так как 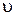D ₃ = D (человек и танк движутся как одно целое), то

.

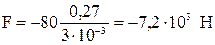О чем говорит знак «минус»? Сила F направлена против скорости и прижимает водителя к сидению.

Ответ: 0,27 м/с; 7,2 кН.

3.6 Задачи по кинематике и динамике вращательного движения решаются так же, как и для поступательного движения. Более того, форма уравнений и законов поступательного и вращательного движений во многом совпадает. При этом роль скорости играет угловая скорость, ускорения – угловое ускорение, силы – момент силы, массы – момент инерции и т. д. Это следует постоянно иметь в виду не только для лучшего усвоения (запоминания) законов вращательного движения, но и для применения общих методик решения задач.

Пример 6. При запуске двигателя автомобиля угол поворота маховика зависит от времени по закону j = А + Bt + Ct², где С = 1,5 рад/с². Радиус маховика 20 см. По касательной к маховику приложена результирующая сила 6 Н. Считая маховик однородным диском, найти его массу.

Дано: СИ Решение

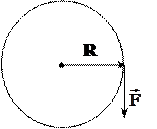
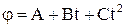
С = 1,5 рад/с²

R = 20 см 0,2 м

F = 6 H

m - ?

Масса маховика определяет его момент инерции

,

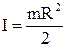который, в свою очередь, входит в основной закон динамики вращательного движения

.

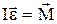Момент силы 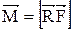. Так как сила в данном случае направлена по касательной, то

.

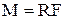Угловое ускорение равно второй производной от угла поворота

.

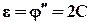Объединяя эти уравнения, получим:

,

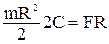откуда 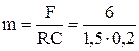= 20 кг.

Ответ: 20 кг.

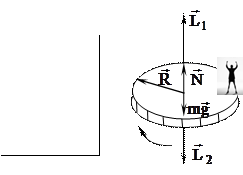Пример 7. Человек массой 70 кг находится на краю неподвижной горизонтальной платформы массой 200 кг и радиусом 1,5 м. Платформа может вращаться вокруг вертикальной оси, проходящей через ее центр. С какой частотой начнет вращаться платформа, если человек спрыгнет с нее в направлении касательной к ободу платформы со скоростью 2 м/с? Платформу считать однородным диском, а человека – точечной массой.

Дано: Решение

m₁ = 70 кг На систему «платформа-человек» действу-

m₂ = 200 кг ют внешние силы: сила тяжести и сила ре-

R = 1,5 м акции опоры, но сумма моментов этих сил

= 2 м/c относительно оси вращения равна нулю,

ν₁ = 0 следовательно, момент импульса системы

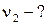остается постоянным.

Момент импульса системы до прыжка равен 0, а после прыжка – сумме моментов импульса человека L₁ и платформы L₂:

.

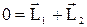Откуда следует, что 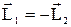, то есть векторы 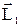и направлены вдоль оси вращения в противоположные стороны.

В скалярном виде L₁= L₂, где 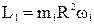– момент импульса человека, которого в данном случае можно считать материальной точкой.

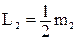
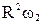– момент импульса платформы.

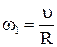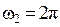
Учитывая, что , , 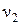получим ,

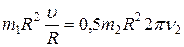откуда 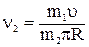, 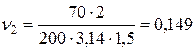об/с = 8,9 об/мин = 0,149 об/с.

Ответ: 0,149 об/c.

Пример 8. Горизонтальная платформа массой 80 кг и радиусом 1 м вращается с угловой скоростью, соответствующей частоте 20 об/мин. В центре платформы стоит человек и держит в горизонтально расставленных руках гири. Какое число оборотов в минуту будет делать платформа, если человек, опустив руки, уменьшит свой момент инерции от 2,94 до 0,98 кгм². Считать платформу круглым однородным диском.

Дано: СИ Решение

m = 80 кг

R = 1 м

2,94 кгм²

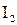= 0,98 кгм²

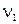= 20 об/мин 0,33 с^-1

- ?

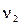В основу решения задачи положим закон сохранения момента импульса:

( + ) = ( + ) ,

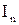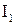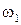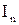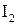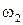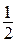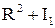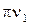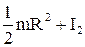то есть ( m ) 2 = ( ) 2 ,

откуда 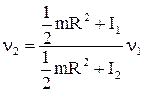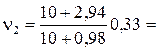0,39 с^-1.

Тогда в минуту ν₂ = 0,39×60 = 23,4 об/мин.

Ответ: 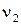= 23,4 мин^-1.

Решение Работа в данной задаче будет равна кинетической энергии шара: A = . Шар совершает сложное вращательно-поступательное движение, поэтому , .

Пример 9. Шар диаметром 6 см катится без скольжения по горизонтальной плоскости, делая 4 об/с. Масса шара 0,25 кг. Какую работу нужно совершить, чтобы остановить шар?

Дано:

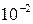d = 6 см = 6× м

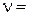4 об\c

m = 0,25 кг

A - ?

Скорость поступательного движения найдём, используя связь линейной и угловой скоростей 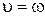R:

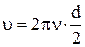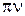= d. Тогда .

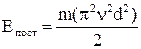Энергия вращательного движения = .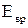

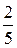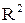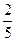Момент инерции шара I = m = m = .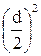

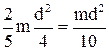Тогда .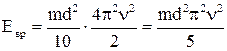

Полная кинетическая энергия:

.

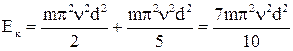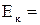0,7×0,25×3,14²×4²×(6×10^-2)² = 0,1 Дж.

Ответ: A = 0,1 Дж.

3.7 Раздел «Молекулярная физика» важен для будущего инженера-автомобилиста тем, что позволяет понимать процессы смесеобразования, сопротивление движению и т. д. Решение многих задач по этому разделу мало чем отличается от того, что изучалось в средней школе. Базой их решения является основное уравнение молекулярно-кинетической теории. Исключение составляют задачи, посвященные явлениям переноса (диффузия, вязкость, теплопроводность), которые изучаются только в высшей школе.

Пример 10. Из баллона со сжатым воздухом объемом 10 л вследствие неисправности вентиля происходит утечка газа. При температуре 7 ⁰С манометр показывает давление 5 МПа, при этом показания манометра не изменились и при температуре 17°С. Какая масса газа вышла из баллона?

Дано: СИ Решение

V = 10 л 10^{-2 м3} Масса газа, вышедшего из баллона, равна раз-

T₁ = 7 ⁰С 280 К ности масс m₁ и m₂ воздуха в баллоне при тем-

p = 5 МПа 5^.10⁶ Па пературах Т₁ и Т₂:

T₂ = 17 ⁰С 290 К .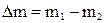

M = 29^.10^-3 кг/моль Массы m₁ и m₂ найдем, используя

p₁ = p₂ уравнение состояния идеального газа

.

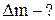
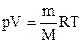Отсюда 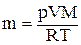. Соответственно, , .

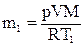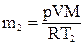Тогда .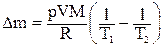

Подставляя числовые значения, получим

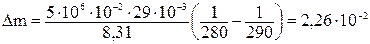кг.

Ответ: 2,26×10^{-2 кг.}

3.8 В разделе «Термодинамика» тепловые процессы рассматриваются с точки зрения энергетических соотношений. Задачи по этому разделу решаются на базе законов термодинамики, в частности, первого закона («начала») термодинамики, известного из курса средней школы. Понимание энергетических характеристик различных изопроцессов и циклов является базой для последующего усвоения циклов тепловых двигателей, в частности, автомобильных.

Здесь следует иметь в виду, что первый закон термодинамики допускает разные формулировки в зависимости от того, рассматриваете ли вы получаемую или отдаваемую теплоту, работу, совершаемую системой, или работу внешних сил. Это разнообразие отражают знаки соответствующих величин А и Q, которые являются алгебраическими.

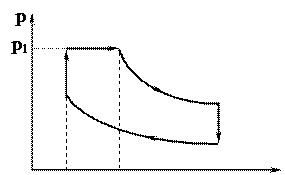Пример 11. Термодинамический цикл двигателя имеет вид, показанный на рисунке. В конце изохорного сгорания при объеме V₁ воздух в цилиндре двигателя имел давление 8 МПа. В процессе изобарного (предварительного) расширения 1 – 2 объем воздуха возрос в 1,5 раза и стал равным 0,124 л. Найти работу, изменение внутренней энергии и теплоту, подведенную к воздуху в процессе предварительного расширения.

Дано: СИ Решение

р₁ = р₂ 1 2

р₁ = 8·10⁶ Па

V₂ = 1,5V₁ = 0,124 л 1,24·10^{-4 м3}

А - ?; ΔU - ?; ΔQ - ?

0 V₁ V₂ V

Работа при изобарном процессе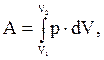

то есть ,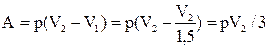

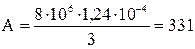Дж.

Приращение внутренней энергии воздуха:

.

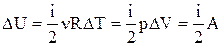Полагая для молекул воздуха i = 5, получим 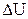= 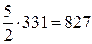Дж.

На основании первого закона термодинамики, полученная воздухом теплота 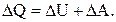Подставляя числовые данные, получим

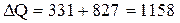Дж.

Ответ: 331 Дж; 827 Дж; 1158 Дж.

Контрольное задание № 1

Вариант контрольного задания студент выбирает из таблицы по первой букве своей фамилии. Вариантом контрольного задания студента является последняя цифра номера зачетной книжки. Например, если фамилия Алексеев, и последняя цифра номера зачетной книжки - 4, то вариант задания – 4, из первой таблицы.

Задание 1

1.1 Зависимость пройденного телом пути от времени дается уравнением

S = At + Bt² + Ct³, где А = 2 м/с, В = 3м/с², С = 4 м/с³. Найти расстояние, пройденное телом, скорость и ускорение тела через 2 с после начала движения.

1.2 Под действием силы 10 Н тело движется прямолинейно так, что зависимость пути от времени дается уравнением S = A - Bt + Ct², где С = 1 м/с². Найти массу тела.

1.3 Материальная точка движется по окружности радиусом 1м согласно уравнению S = 8t - 0,2t³. Найти скорость, тангенциальное, нормальное и полное ускорение в момент времени 3 с.

1.4 Автомобиль, имея скорость 18 км/ч, разгонялся в течение 10 с с ускорением а = Аt³, где А = 0,01 м/с⁵. Найти его среднюю скорость за время ускорения и мгновенную скорость в конце этого времени.

1.5 Зависимость пройденного телом пути от времени дается уравнением S = A + Bt + Ct² + Dt³, где С = 0,14 м/с² и D = 0,01 м/с³. Через какое время после начала движения тело будет иметь ускорение 1 м/с²? Найти среднее ускорение тела за этот промежуток времени.

1.6 Под действием какой силы при прямолинейном движении тела массой 2 кг изменение его координаты со временем происходит по закону

х = 10 + 5t – 10t²?

1.7 Автомобиль движется по закруглению шоссе, имеющему радиус кривизны 100 м. Закон движения выражается уравнением S = 100 + 10t – 0,5t² . Найти скорость автомобиля, его тангенциальное, нормальное и полное ускорение в конце пятой секунды.

1.8 Материальная точка движется по окружности, радиус которой 20 м. Зависимость пути, пройденного точкой, от времени выражается уравнением S = t³ + 4t² – t + 8. Определить пройденный путь, угловую скорость и угловое ускорение точки через 3 с от начала ее движения.

1.9 Материальная точка движется по окружности радиуса 1 м согласно уравнению S = 8t – 0,2t³. Найти скорость, тангенциальное, нормальное и полное ускорение в момент времени 3с.

1.10 Точка движется по окружности радиусом 4 м. Закон ее движения выражается уравнением х = 8 – 2t². Найти момент времени, когда нормальное ускорение точки равно 9 м/с², скорость, тангенциальное и полное ускорение точки в этот момент времени.

Задание 2

2.1 Тело брошено со скоростью V₀ под углом к горизонту. Время полета 2,2 с. На какую высоту поднимется тело?

2.2 Мяч брошен со скоростью 10 м/с под углом 40⁰ к горизонту. На какую высоту поднимется мяч? Какое время он будет в движении?

2.3 Камень, брошенный горизонтально, через 0,5 с после начала движения имел скорость в 1,5 раза большую скорости в момент бросания. С какой скоростью брошен камень?

2.4 Камень брошен горизонтально со скоростью 10 м/с. Найти радиус кривизны траектории камня через 3 с после начала движения.

2.5 Тело брошено со скоростью V₀ под углом α к горизонту. Найти скоростьV₀ и угол α, если известно, что высота подъема тела 3 м и радиус кривизны траектории тела в верхней точке траектории равен 3 м.

2.6 Тело брошено со скоростью 15 м/с под углом 30⁰ к горизонту. Пренебрегая сопротивлением воздуха, определите наибольшую высоту подъема тела, дальность полета по горизонтали, время его движения.

2.7 Тело брошено со скоростью 20 м/с под углом 30⁰ к горизонту. Пренебрегая сопротивлением воздуха, определите для момента времени 1,5 с после начала движения нормальное и тангенциальное ускорение.

2.8 С башни высотой 40 м брошено тело со скоростью 20 м/с под углом 45⁰ к горизонту. Пренебрегая сопротивлением воздуха, определите время движения тела. На каком расстоянии от основания башни тело упадет на землю?

2.9 С башни высотой 20 м брошено тело со скоростью 10 м/с под углом 60⁰ к горизонту, пренебрегая сопротивлением воздуха, определите время движения тела. С какой скоростью тело упадет на землю?

2.10 Тело брошено горизонтально со скоростью 5 м/с. Пренебрегая сопротивлением воздуха, определите радиус кривизны траектории тела через 2 с после начала движения.

Задание 3

3.1 Тело скользит по наклонной плоскости, составляющей с горизонтом угол 45^°. Пройдя путь 36,4 см, тело приобретает скорость 2 м/с. Найти коэффициент трения тела о плоскость.

3.2 На автомобиль массой 1 т во время движения действует сила трения, равная 0,1 действующей на него силы тяжести. Найти силу тяги, развиваемую мотором автомобиля, если автомобиль движется с постоянной скоростью в гору с уклоном 1 м на каждые 25 м пути.

3.3 Тело скользит по наклонной плоскости, составляющей с горизонтом угол 45^°. Зависимость пройденного телом пути от времени дается уравнением

S = Ct², где С = 1,73 м/с². Найти коэффициент трения тела о плоскость.

3.4 Тело скользит сначала по наклонной плоскости, составляющей угол 8^° с горизонтом, а затем по горизонтальной поверхности. Найти коэффициент трения на всем пути, если известно, что тело проходит по горизонтальной поверхности то же расстояние, что и по наклонной плоскости.

3.5 Две гири с массами 2 кг и1 кг соединены нитью и перекинуты через невесомый блок. Найти ускорение, с которым движутся гири, и силу натяжения нити. Трением в блоке пренебречь.

3.6 К нити подвешен груз массой 500 г. Определите силу натяжения нити, если нить с грузом: а)поднимать с ускорением 2 м/с²; б)опускать с ускорением 2 м/с².

3.7 Два груза массами 500 г и 700 г соответственно связаны невесомой нитью и лежат на гладкой горизонтальной поверхности. К одному из грузов приложена горизонтально направленная сила 6 Н. Пренебрегая трением, определите ускорение грузов и силу натяжения нити.

3.8 Тело массой 2 кг падает вертикально с ускорением 5 м/с². Определите силу сопротивления при движении этого тела.

3.9 По наклонной плоскости с углом наклона к горизонту, равным 30^°, скользит тело. Определите скорость тела в конце второй секунды от начала скольжения, если коэффициент трения 0,15.

3.10 Вагон массой 1 т спускается по канатной железной дороге с уклоном 15^° к горизонту. Принимая коэффициент трения 0,05, определите силу натяжения каната при торможении вагона в конце спуска, если скорость вагона перед торможением 2,5 м/с, а время торможения 6 с.

Задание 4

4.1 Из ружья массой 5 кг вылетает пуля массой 5 г со скоростью 600 м/с. Найти скорость отдачи ружья.

4.2 Камень, пущенный по поверхности льда со скоростью 3 м/с, прошел до остановки расстояние 20,4 м. Найти коэффициент трения камня о лед.

4.3 Снаряд массой 100 кг, летящий горизонтально вдоль железнодорожного пути со скоростью 520 м/с, попадает в вагон с песком, масса которого10 т, и застревает в нем. Какую скорость получит вагон, если: а) он стоял неподвижно; б) вагон двигался со скоростью 36 км/ч в том же направлении, что и снаряд?

4.4 Человек массой 60 кг, бегущий со скоростью 8 км/ч, догоняет тележку массой 80 кг, движущуюся со скоростью 2,9 км/ч, и вскакивает на нее. С какой скоростью будет двигаться тележка? С какой скоростью двигалась бы тележка, если бы человек бежал ей навстречу?

4.5 С покоящимся шаром массой 2 кг сталкивается такой же шар, движущийся со скоростью 1 м/с. Вычислить работу, совершаемую вследствие деформации при прямом центральном неупругом ударе.

4.6 Снаряд массой 5 кг, вылетевший из орудия, в верхней точке траектории имеет скорость 300 м/с. В верхней точке он разорвался на два осколка, причем больший осколок массой 3 кг полетел в обратном направлении со скоростью 100 м/с. Определите скорость второго осколка.

4.7 Лодка массой 150 кг и длиной 2,8 м неподвижна в стоячей воде. Рыбак массой 90 кг в лодке переходит с носа на корму. Пренебрегая сопротивлением воды, определите, на какое расстояние при этом сдвинется лодка.

4.8 Платформа с песком общей массой 2 т стоит на рельсах на горизонтальном участке пути. В песок попадает снаряд массой 8 кг и застревает в нем. Пренебрегая трением, определите, с какой скоростью будет двигаться платформа, если в момент попадания скорость снаряда 450 м/с, а ее направление – сверху вниз под углом 30^°к горизонту.

4.9 На железнодорожной платформе, движущейся со скоростью 3 км/ч, укреплено орудие. Масса платформы с орудием 10 т. Ствол орудия направлен в сторону движения платформы. Снаряд массой 10 кг вылетает из ствола под углом 60^° к горизонту. Определите скорость снаряда, если после выстрела скорость платформы уменьшилась в 2 раза.

4.10 Орудие, жестко закрепленное на железнодорожной платформе, производит выстрел вдоль полотна железной дороги под углом 45^° к линии горизонта. Определить скорость отката платформы, если снаряд вылетает со скоростью 480 м/с. Масса платформы с орудием и снарядами равна 18 т, масса снаряда – 60кг.

Задание 5

5.1 Мяч, летящий со скоростью 15 м/с, отбрасывается ударом ракетки в противоположном направлении со скоростью 20 м/с. Найти изменение импульса мяча, если известно, что изменение его кинетической энергии 8,7 Дж.

5.2 Диск вращается вокруг вертикальной оси с частотой 30 об/мин. На расстоянии 20 см от оси вращения на диске лежит тело. Каким должен быть коэффициент трения между телом и диском, чтобы тело не скатилось с диска?

5.3 Найти работу, которую надо совершить, чтобы сжать пружину на

20 см, если известно, что сила пропорциональна сжатию и жесткость пружины 2,94 кН/м.

5.4 Стальной шарик массой 20 г падает с высоты 1 м на стальную плиту, отскакивает от нее на высоту 81 см. Найти импульс силы, полученный плитой за время удара, и количество теплоты, выделившееся при ударе.

5.5 Какую массу бензина расходует двигатель автомобиля на пути 100 км, если при мощности двигателя 11 кВт скорость его движения 30 км/ч? КПД двигателя 0,22, удельная теплота сгорания бензина 46 МДж/кг.

5.6 Гиря массой 10 кг падает с высоты 0,5 м на подставку, скрепленную с пружиной жесткостью 30 Н/см. Определите при этом смещение пружины.

5.7 Тело, падая с некоторой высоты, в момент соприкосновения с землей обладает импульсом 100 кг×м/с и кинетической энергией 500 Дж. Определите с какой высоты упало тело и его массу.

5.8 Поезд массой 600 т движется под гору с уклоном 0,3^° и за 1 мин развивает скорость 18 кмч. Коэффициент трения 0,01. Определите среднюю мощность локомотива.

5.9 Тело массой 5 кг поднимают с ускорением 2 мс². Определите работу силы в течение первых пяти секунд.

5.10 Тело брошено вертикально вверх со скоростью 20 мс. Пренебрегая сопротивлением воздуха, определите, на какой высоте кинетическая энергия тела составляет третью часть от его потенциальной энергии.

Задание 6

6.1 Гирька, привязанная к нити длиной 30 см, описывает в горизонтальной плоскости окружность радиусом 15 см. С какой частотой вращается гирька?

6.2 Определить кинетическую энергию цилиндра, который катится без скольжения по горизонтальной поверхности со скоростью 10 м/с. Масса цилиндра 1 кг.

6.3 Колесо, вращаясь равноускоренно, достигло угловой скорости

20 рад/с через 10 оборотов после начала вращения. Найти угловое ускорение колеса.

6.4 Найти радиус вращающегося колеса, если известно, что линейная скорость точки, лежащей на ободе, в 2,5 раза больше линейной скорости точки, лежащей на расстоянии 5 см ближе к оси колеса.

6.5 Колесо вращается с угловым ускорением 2 рад/с². Через 0,5 с после начала движения полное ускорение колеса составило 13,6 см/с². Найти радиус колеса.

6.6 К ободу однородного сплошного диска массой 10 кг, насаженного на ось, приложена постоянная касательная сила 30 Н. Определите кинетическую энергию диска через 4 с после начала действия силы.

6.7 Вентилятор вращается с частотой 600 об/мин. После выключения он начал вращаться равнозамедленно и, сделав 50 оборотов, остановился. Работа сил торможения равна 31,4 Дж. Определите момент сил торможения и момент инерции вентилятора.

6.8 Маховик в виде сплошного диска, момент инерции которого

150 кг×м², вращается с частотой 240 об/мин. Через 1 мин, как на маховик стал действовать момент сил торможения, он остановился. Определить момент сил торможения и число оборотов, совершенных маховиком от начала торможения до полной остановки.

6.9 На обод маховика диаметром 60 см намотан шнур, к концу которого привязан груз массой 2 кг. Определить момент инерции маховика, если он, вращаясь равноускоренно под действием силы тяжести груза, за 3 с приобрел угловую скорость 9 рад/с.

6.10 Определить момент силы, который необходимо приложить к блоку, вращающемуся с частотой 12 с^-1, чтобы он остановился в течение 8 с. Диаметр блока 30 см, масса 6 кг. Блок считать полым цилиндром.

Задание 7

7.1 Кинетическая энергия вала, вращающегося с частотой 5 с^-1,60 Дж. Найти момент импульса вала.

7.2 Чему равен момент импульса шара радиусом 10 см, если он вращается вокруг оси, проходящей через его центр с частотой 2 с^-1.

7.3 Найти кинетическую энергию велосипедиста, едущего со скоростью 9 км/ч. Масса велосипедиста вместе с велосипедом 78 кг, причем на колеса приходится масса 3 кг. Колеса велосипеда считать обручами.

7.4 Диск массой 2 кг катится без скольжения по горизонтальной плоскости со скоростью 4 м/с. Найти кинетическую энергию диска.

7.5 Маховик, имеющий форму диска массой 10 кг и радиусом 0,1 м, был раскручен до частоты 120 мин^-1. Под действием силы трения диск остановился через 10 с. Найти момент силы трения, считая его постоянным.

7.6 Вентилятор вращается с частотой 600 об/мин. После выключения он начал вращаться равнозамедленно и, сделав 50 оборотов, остановился. Работа сил торможения равна 31,4 Дж. Определите момент сил торможения и момент инерции вентилятора.

7.7 На краю неподвижной скамьи Жуковского диаметром 0,8 м и массой 6 кг стоит человек массой 60 кг. С какой угловой скоростью начнет вращаться скамья, если человек поймает летящий на него мяч максой 0,5 кг? Траектория мяча горизонтальна и проходит на расстоянии 0,4 м от оси скамьи. Скорость мяча 5 м/с.

7.8 На скамье Жуковского стоит человек и держит в руках стержень вертикально по оси вращения скамьи. Скамья с человеком вращается с угловой скоростью 4 рад/с. С какой угловой скоростью будет вращаться скамья с человеком, если повернуть стержень так, чтобы он занял горизонтальное положение? Суммарный момент инерции человека и скамьи 5 кг×м². Длина стержня

1,8 м и его масса 6 кг. Считать, что центр тяжести стержня с человеком находится на оси платформы.

7.9 Платформа в виде диска диаметром 3 м и массой 180 кг может вращаться вокруг вертикальной оси. С какой угловой скоростью будет вращаться платформа, если по ее краю пойдет человек массой 70 кг со скоростью 1,8 м/с относительно платформы?

7.10 Платформа, имеющая форму диска, может вращаться около вертикальной оси. На краю платформы стоит человек. На какой угол повернется платформа, если человек пойдет вдоль края платформы и, обойдя ее, вернется в исходную (на платформе) точку? Масса платформы 280 кг, масса человека

80 кг. Момент инерции человека рассчитывать как для материальной точки.

Задание 8

8.1 Во сколько раз плотность воздуха, заполняющего помещение зимой (температура 7 °С ), больше его плотности летом (температура 3 °С ). Давление газа считать постоянным.

8.2 В сосуде объемом 2 л находятся 6 г углекислого газа и 4 г окиси азота при температуре 127 °С. Найти давление смеси в сосуде.

8.3 Молекула азота летит со скоростью 430 м/с. Найти импульс этой молекулы.

8.4 В баллоне находилось 10 кг газа при давлении 10 Мпа. Какую массу газа взяли из баллона, если давление стало равным 2,5 Мпа? Температуру газа считать постоянной.

8.5 Сосуд откачан до давления 1,33^.10^-9 Па; температура воздуха 15 °С. Найти плотность воздуха в сосуде.

8.6 В баллоне емкостью 50 л находится сжатый водород при 27 °С. После того как часть водорода выпустили, давление понизилось на 1×10⁵ Па. Определить массу выпущенного водорода. Процесс считать изотермическим.

8.7 При температуре 300 К и давлении 1,2×10⁵ Па плотность смеси водорода и азота 1 кг/м³. Определить молярную массу смеси.

8.8 При температуре 300 К и давлении 10⁶ Па плотность смеси кислорода и азота 15 г/дм³. Определить молярную массу смеси.

8.9 В баллоне емкостью 0,8 м³ находятся 2 кг водорода и 2,9 кг азота. Определить давление смеси, если температура окружающей среды 27 °С.

8.10 В сосуде, имеющем форму шара, радиус которого 0,1 м, находится 56 г азота. До какой температуры можно нагреть сосуд, если его стенки выдерживают давление 5×10⁵ Па?

Задание 9

9.1 При изотермическом расширении 10 г азота, находящегося при температуре 17 °С, была совершена работа 860 Дж. Во сколько раз изменилось давление азота при расширении?

9.2 Азоту массой 20 г при изобарическом нагревании сообщили 3116 Дж теплоты. Как изменились температура и внутренняя энергия газа?

9.3 Водород массой 6,5 г, находящийся при температуре 27 °С, расширяется вдвое при постоянном давлении за счет притока тепла извне. Найти работу расширения газа, изменение внутренней энергии и количество теплоты, сообщенное газу.

9.4 В закрытом сосуде находятся 20 г азота и 32 г кислорода. Найти изменение внутренней энергии смеси газов при охлаждении ее на 28 К.

9.5 Найти среднюю кинетическую энергию вращательного движения всех молекул, содержащихся в 0,20 г водорода при температуре 27 °С.

9.6 Найти среднюю кинетическую энергию поступательного движения всех молекул, содержащихся в 0,20 г водорода при температуре 27 °С.

9.7 Давление идеального газа 10 мПа, концентрация молекул 8×10¹⁰ см^-3. Определить среднюю кинетическую энергию поступательного движения одной молекулы и температуру газа.

9.8 Определить среднее значение полной кинетической энергии одной молекулы аргона и водяного пара при температуре 500 К.

9.9 Азот массой 10 г находится при температуре 290 К. Определить среднюю кинетическую энергию одной молекулы азота и среднюю кинетическую энергию вращательного движения всех молекул азота. Газ считать идеальным.

9.10 В закрытом сосуде находится смесь азота массой 56 г и кислорода массой 64 г. Определите изменение внутренней энергии этой смеси, если ее охладили на 20 °С.

Задание 10

10.1 Идеальная тепловая машина работает по циклу Карно. При этом

80 % количества теплоты, получаемого от нагревателя, передается холодильнику. Машина получает от нагревателя количество теплоты 6280 Дж. Найти КПД цикла и работу, совершаемую за один цикл.

10.2 Совершая цикл Карно, газ отдал холодильнику 0,25 теплоты, полученной от нагревателя. Определить температуру холодильника, если температура нагревателя 400 К.

10.3 При прямом цикле Карно тепловая машина совершает работу

1000 Дж. Температура нагревателя 500 К, температура холодильника 300 К. Определить количество теплоты, получаемое машиной от нагревателя.

10.4 Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу 2,94 кДж и отдает холодильнику количество теплоты 13,4 кДж. Найти КПД цикла.

10.5 Тепловая машина работает по циклу Карно, КПД которого 0,4. Каков будет КПД этой машины, если она будет совершать тот же цикл в обратном направлении?

10.6 Идеальный газ, совершающий цикл Карно, 70 % количества теплоты, полученной от нагревателя, отдает холодильнику. Количество теплоты, получаемое от нагревателя, равно 5 кДж. Определите термический КПД цикла и работу, совершенную при полном цикле.

10.7 Идеальный газ совершает цикл Карно. Газ получил от нагревателя количество теплоты 5,5 кДж. Определите термический КПД цикла и отношение температур нагревателя и холодильника.

10.8 Идеальный газ совершает цикл Карно, термический КПД которого равен 0,4. Определите работу изотермического сжатия газа, если работа изотермического расширения составляет 400 Дж.

10.9 Идеальный газ совершает цикл Карно. Температура нагревателя

500 К, холодильника 300 К. Работа изотермического расширения газа составляет 2 кДж. Определите термический КПД цикла, количество теплоты, отданное газом холодильнику при изотермическом сжатии.

10.10 Многоатомный идеальный газ совершает цикл Карно, при этом в процессе адиабатного расширения объем газа увеличивается в 4 раза. Определите термический КПД цикла.

Распределение заданий по вариантам КЗ № 1

для студентов, фамилии которых начинаются с букв А, Б, В, Г, Д, Е, Ж

Последняя цифра в № зачетной книжки
Задание 1	1.3	1.4	1.5	1.6	1.7	1.8	1.9	1.10	1.1	1.2
Задание 2	2.6	2.7	2.8	2.9	2.10	2.1	2.2	2.3	2.4	2.5
Задание 3	3.9	3.10	3.1	3.2	3.3	3.4	3.5	3.6	3.7	3.8
Задание 4	4.2	4.3	4.4	4.5	4.6	4.7	4.8	4.9	4.10	4.1
Задание 5	5.5	5.6	5.7	5.8	5.9	5.10	5.1	5.2	5.3	5.4
Задание 6	6.8	6.9	6.10	6.1	6.2	6.3	6.4	6.5	6.6	6.7
Задание 7	7.1	7.2	7.3	7.4	7.5	7.6	7.7	7.8	7.9	7.10
Задание 8	8.4	8.5	8.6	8.7	8.8	8.9	8.10	8.1	8.2	8.3
Задание 9	9.7	9.8	9.9	9.10	9.1	9.2	9.3	9.4	9.5	9.6
Задание 10	10.10	10.1	10.2	10.3	10.4	10.5	10.6	10.7	10.8	10.9

для студентов, фамилии которых начинаются с букв З, И, К, Л, М, Н

Последняя цифра в № зачетной книжки
Задание 1	1.10	1.1	1.2	1.3	1.4	1.5	1.6	1.7	1.8	1.9
Задание 2	2.10	2.1	2.2	2.3	2.4	2.5	2.6	2.7	2.8	2.9
Задание 3	3.10	3.1	3.2	3.3	3.4	3.5	3.6	3.7	3.8	3.9
Задание 4	4.10	4.1	4.2	4.3	4.4	4.5	4.6	4.7	4.8	4.9
Задание 5	5.10	5.1	5.2	5.3	5.4	5.5	5.6	5.7	5.8	5.9
Задание 6	6.10	6.1	6.2	6.3	6.4	6.5	6.6	6.7	6.8	6.9
Задание 7	7.10	7.1	7.2	7.3	7.4	7.5	7.6	7.7	7.8	7.9
Задание 8	8.10	8.1	8.2	8.3	8.4	8.5	8.6	8.7	8.8	8.9
Задание 9	9.10	9.1	9.2	9.3	9.4	9.5	9.6	9.7	9.8	9.9
Задание 10	10.10	10.1	10.2	10.3	10.4	10.5	10.6	10.7	10.8	10.9

для студентов, фамилии которых начинаются с букв О, П, Р, С, Т, У, Ф

Последняя цифра в № зачетной книжки
Задание 1	1.1	1.2	1.3	1.4	1.5	1.6	1.7	1.8	1.9	1.10
Задание 2	2.2	2.3	2.4	2.5	2.6	2.7	2.8	2.9	2.10	2.1
Задание 3	3.3	3.4	3.5	3.6	3.7	3.8	3.9	3.10	3.1	3.2
Задание 4	4.4	4.5	4.6	4.7	4.8	4.9	4.10	4.1	4.2	4.3
Задание 5	5.5	5.6	5.7	5.8	5.9	5.10	5.1	5.2	5.3	5.4
Задание 6	6.6	6.7	6.8	6.9	6.10	6.1	6.2	6.3	6.4	6.5
Задание 7	7.7	7.8	7.9	7.10	7.1	7.2	7.3	7.4	7.5	7.6
Задание 8	8.8	8.9	8.10	8.1	8.2	8.3	8.4	8.5	8.6	8.7
Задание 9	9.9	9.1	9.1	9.2	9.3	9.4	9.5	9.6	9.7	9.8
Задание 10	10.10	10.2	10.2	10.3	10.4	10.5	10.6	10.7	10.8	10.9

для студентов, фамилии которых начинаются с букв Х, Ц, Ч, Ш, Щ, Э, Ю, Я

Последняя цифра в № зачетной книжки
Задание 1	1.2	1.3	1.4	1.5	1.6	1.7	1.8	1.9	1.10	1.1
Задание 2	2.4	2.5	2.6	2.7	2.8	2.9	2.10	2.1	2.2	2.3
Задание 3	3.6	3.7	3.8	3.9	3.10	3.1	3.2	3.3	3.4	3.5
Задание 4	4.8	4.9	4.10	4.1	4.2	4.3	4.4	4.5	4.6	4.7
Задание 5	5.10	5.1	5.2	5.3	5.4	5.5	5.6	5.7	5.8	5.9
Задание 6	6.2	6.3	6.4	6.5	6.6	6.7	6.8	6.9	6.10	6.1
Задание 7	7.4	7.5	7.6	7.7	7.8	7.9	7.10	7.1	7.2	7.3
Задание 8	8.6	8.7	8.8	8.9	8.10	8.1	8.2	8.3	8.4	8.5
Задание 9	9.8	9.9	9.10	9.1	9.2	9.3	9.4	9.5	9.6	9.7
Задание 10	10.10	10.1	10.2	10.3	10.4	10.5	10.6	10.7	10.8	10.9
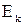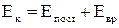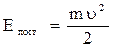