При вращательном движении твердого тела под действием силы F работа равняется произведению момента этой силы на угол поворота

12) Специальная теория относительности— теория, описывающая движение, законы механики и пространственно-временные отношения при произвольных скоростях движения, меньших скорости света в вакууме, в том числе близких к скорости света.

В расширенной специальной теории относительности (РСТО) система аксиом имеет следующий вид:

· Выполнение принципа относительности (если все материальные тела физической системы привести в состояние свободного и равномерного прямолинейного движения относительно системы, условно называемой покоящейся, то явления в движущейся системе отсчёта для сопутствующего наблюдателя будут выглядеть так же, как в покоящейся системе отсчёта для неподвижного в ней наблюдателя).

· Существует такая изотропная система отсчёта, в которой скорость распространения света одинакова по всем направлениям и не зависит от скорости излучателя света.

· Справедливость симметрий относительно поворотов в пространстве-времени Евклида. В частности, при движении системы отсчёта оси координат считаются остающимися параллельными осям неподвижной системы отсчёта. Также подразумевается независимость скорости света от направления его распространения в поперечном направлении относительно скорости движения инерциальной системы отсчёта.

· Справедливость симметрий относительно сдвигов в пространстве-времени Евклида. Это означает линейность преобразований координат и времени из одной инерциальной системы отсчёта в другую (все координаты в преобразованиях входят в первой степени, члены с более высокими степенями отсутствуют). Кроме этого считается, что поперечная длина стержня не зависит от знака скорости перемещения этого стержня, а определяется абсолютным значением скорости.

· Пространственно-временные измерения осуществляются с помощью электромагнитных волн.

Преобразованиями Лоренца в физике, в частности, в специальной теории относительности (СТО), называются преобразования, которым подвергаются пространственно-временные координаты (x,y,z,t) каждого события при переходе от одной инерциальной системы отсчета (ИСО) к другой. Аналогично, преобразованиям Лоренца при таком переходе подвергаются координаты любого 4-вектора.Чтобы явно различить преобразования Лоренца со сдвигами начала отсчёта и без сдвигов, когда это необходимо, говорят о неоднородных и однородных преобразованиях Лоренца.Преобразования Лоренца без сдвигов начала отсчёта образуют группу Лоренца, со сдвигами — группу Пуанкаре, иначе называемую неоднородной группой Лоренца.С математической точки зрения преобразования Лоренца — это преобразования, сохраняющие неизменной метрику Минковского, то есть, в частности, последняя сохраняет при них простейший вид при переходе от одной инерциальной системы отсчёта к другой (другими словами преобразования Лоренца — это аналог для метрики Минковского ортогональных преобразований, осуществляющих переход от одного ортонормированного базиса к другому, то есть аналог поворота координатных осей для пространства-времени). В математике или теоретической физике преобразования Лоренца могут относиться к любой размерности пространства.Именно преобразования Лоренца, смешивающие — в отличие от преобразований Галилея — пространственные координаты и время, исторически стали основой для формирования концепции единого пространства-времени.

· Следует заметить, что лоренц-ковариантны не только фундаментальные уравнения (такие, как уравнения Максвелла, описывающее электромагнитное поле, уравнение Дирака, описывающее электрон и другие фермионы), но и такие макроскопические уравнения, как волновое уравнение, описывающее (приближенно) звук, колебания струн и мембран, и некоторые другие (только тогда уже в формулах преобразований Лоренца под c следует иметь в виду не скорость света, а какую-то другую константу, например скорость звука). Поэтому преобразования Лоренца могут быть плодотворно использованы и в связи с такими уравнениями (хотя и в довольно формальном смысле, впрочем, мало отличающемся — в своих рамках — от их применения в фундаментальной физике).

14) Релятивистская Динамика-раздел частной теории относительности, посвященный изучению движения материальных тел под действием приложенных к ним сил. В теории относительности свободные, т. е. не подверженные действию сил, материальные точки имеют в качестве своих мировых линий времениподобные или изотропные геодезические. Этот факт является выражением закона инерции в теорий относительности. Если на частицу действуют силы, то ее мировая линия не совпадает с геодезической. Для описания движения частицы вводятся понятия четырехмерного вектора энергии-импульса р i и вектора четырехмерной силы gi. Именно, (1) где Е - энергия частицы, m - масса покоя, - трехмерный импульс частицы. Вектор gi' определяется соотношением где -трехмерная сила, -скорость. С использованием этих векторов основные уравнения Р. д. могут быть записаны в виде, аналогичном виду уравнений второго закона Ньютона: (2) Конкретный вид силы gi устанавливается в тех разделах теории относительности, к-рые изучают конкретные свойства различных взаимодействий. Напр., сила, действующая на частицу в электромагнитном поле - с и л а Л о р е н ц а, имеет вид где е - заряд частицы, - тензор электромагнитного поля, - четырехмерная скорость.

Эквивале́нтность ма́ссы и эне́ргии— физическая концепция, согласно которой масса тела является мерой энергии, заключённой в нём. Энергия тела равна массе тела, умноженной на размерный множитель квадрата скорости света в вакууме: 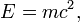где E — энергия тела, m — его масса, c — скорость света в вакууме, равная 299 792 458 м/с.

15) Молекулярная физика — раздел физики, который изучает физические свойства тел на основе рассмотрения их молекулярного строения. Задачи молекулярной физики решаются методами физической статистики, термодинамики и физической кинетики, они связаны с изучением движения и взаимодействия частиц (атомов, молекул, ионов), составляющих физические тела.