Electromagnetic free damped oscillations
The aim is to determine the logarithmic decrement and damping factor of electric oscillations.
Instrumentation and appliances: an electric oscillating circuit, oscillograph.
Short theory
The processes of transforming electric energy into magnetic energy and vice versa are of fundamental importance in electrodynamics. A simple system in which such transformations occur is a charged electric condenser whose plates are connected at a certain instant to a coil. When the condenser discharges, an electric current flows through the coil and creates a magnetic field around it. At each instant, the electric field of the condenser and the magnetic field of the coil are linked.
Let us consider an electric oscillating circuit, i.e. a circuitry consisting of a coil of inductance L and a condenser of capacitance C and the resistance R.
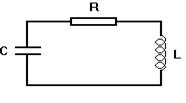
Figure 20.1
The electric current flows through the conductors with a finite velocity. Thus the motion of the charges which begins at some definite time on the condenser plates, reaches the coil at a short time Dt later, where Dt depends on the velocity of propagation of the current and the length of the wires. This means that the current intensity in different parts of the circuit will be different. A change in voltage at the condenser plates does not immediately reach the coil, but at a short time later; in exactly the same way, the self-induced e.m.f. arising at some fixed time in the coil reaches the condenser a short time after. However, if the dimensions of the circuit
are small, then the speed of the change in the current intensity is not very large, then it is reasonable to suppose that the current intensity is the same everywhere in the circuit at a fixed time.
In such a case we may use the second Kirchhoff's Law for a closed circuit: the algebraic sum of all the e.m.f. and the drop in voltage is equal to zero at a given time. This law is true only for constant currents; if the current intensity in the circuit changes, then the application of this law results in a larger error the faster the current changes and the larger the dimensions of the circuit.
The self-induced e.m.f. has a sign opposite to the sign of the potential difference on the condenser plates, so that Kirchhoff’s Law is written as
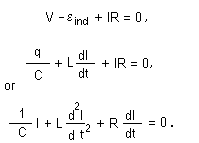
At this point, an analogy should be drawn between the corresponding electric and mechanical quantities. Comparing the last equation with the equation for mechanical oscillations with friction, it is seen that the electric resistance is analogous to the resistance coefficient r, which is a measure of the mechanical resistance. We shall simply give the final result of the solution of the last linear differential equation, which incidentally is easily verified by substitution in the above equation:
I = I0 e-b t coswt.
The frequency of oscillation is given by
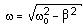 .
.
Thus, the process is determined by two characteristics - the natural frequency of free undamped oscillations
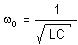
and the damping coefficient b = R/2L. It will be noted that when
w02 < b2, i.e., 4L< CR2
oscillations become impossible.
The difference of voltage on the condenser plates varies according to the law
U = U0e-b tsin wt.
Then the amplitude of such oscillations is
U = U0e-b tsin wt
After logarithming this expression we obtain
Ln Um = ln U0 - b t.
Thus, the damping factor b is equal
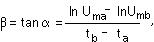
where a is the angle how it shows fig.20.2:
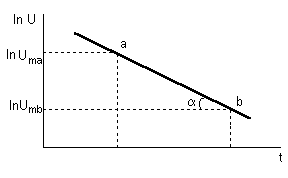
Figure 20.2
The logarithmic decrement we obtain from formula
l = b T.
The electric circuit shown in fig.20.3 may be used to measure the dependence of a difference of voltage versus a time.
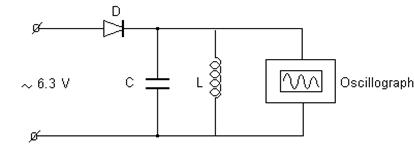
Figure 20.3
Experimental part
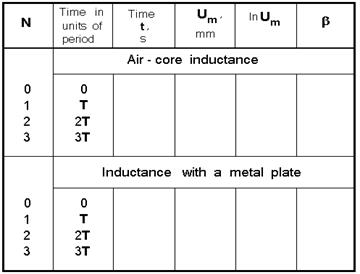
1. Measure the amplitudes of electric oscillations as it is shown in figure 20.4. Put down the values of measurements in table 20.1.
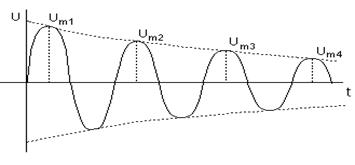
Figure 20.4
2. Put down the metal plate on the inductance. Measure the amplitudes of electric oscillation. Put down the date of measurement in table 20.1.
3. Plot the graph, plotting ln Um against a time t for two cases:
a) air-core inductance;
b) inductance with a metal plate.
Table 20.1
 .
.
4. Calculate the damping factor and logarithmic decrements for two cases if T = 0.5 ms.
5. Make analysis of the experimental results.
Control questions
1. What is damped oscillations?
2. What are the logarithmic decrement and the damping factor?
3. Calculate the velocity and acceleration for damped oscillatory motion.
4. Obtain the expressions for the frequency and period of damped oscillations.
Translator: S.P. Lushchin, the reader, candidate of physical and mathematical sciences.
Reviewer: S.V. Loskutov, professor, doctor of physical and mathematical sciences.
Approved by the chair of physics. Protocol № 6 from 30.03.2009 .
ЛАБОРАТОРНА РОБОТА № 46
РЕЗОНАНС У КОЛИВАЛЬНОМУ КОНТУРІ
Мета роботи: вивчення вимушених коливань та явища резонансу в коливальному контурі
Завдання: одержати залежність напруги uс на конденсаторі від частоти w прикладеної напруги і побудувати графік uc = f(w). Визначити резонансну частоту w0 та перевірити формулу резонансної кривої.
Прилади і обладнання: коливальний контур, генератор синусоїдальних коливань ГНЧШ (вихід – 5 Ом), частотомір, мілівольтметр.
