Розділ 10. Нерівноважна термодинаміка
10.1. Нерівноважна система локально нерівноважна, якщо не виконуються умови локальної рівноваги (10.1) та (10.2), тобто при 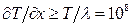 К/см,
К/см, 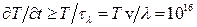 К/с.
К/с.
Частина друга. СТАТИСТИЧНА ФІЗИКА
Розділ 11. Вихідні положення і основні рівняння класичної статистичної фізики
11.1.Умова нормування має вигляд:
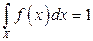 , де
, де 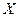 – спектр випадкової величини
– спектр випадкової величини 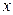 .
.
а) 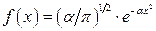 ; врахувати результат задачі 1 цього розділу;
; врахувати результат задачі 1 цього розділу;
б) 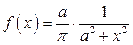 ;
;
в) 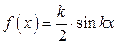 ;
;
г) 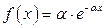 ;
;
д) 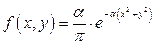 .
.
11.2. Для обчислення середніх значень 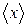 та дисперсій
та дисперсій 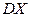 слід скористатися формулами:
слід скористатися формулами:
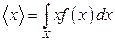 ,
, 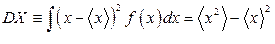 .
.
а) 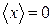 ,
, 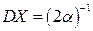 ;
;
б) 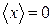 ,
, 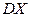 не існує, оскільки відповідний інтеграл розбігається;
не існує, оскільки відповідний інтеграл розбігається;
в) 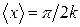 ,
, 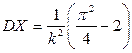 ;
;
г) 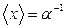 ,
, 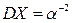 .
.
11.3. 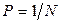 .
.
11.4. 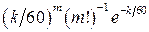 .
.
11.5. Розгляньте малюнки:
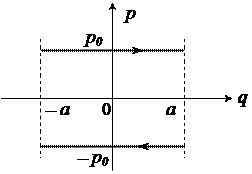
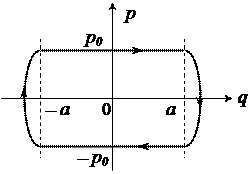
а) б)
11.6. Фазовою траєкторією частинки, що вертикально падає, є парабола, рівняння якої (у змінних 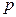 ,
, 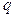 ):
):
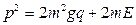 , де
, де 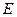 – повна енергія частинки,
– повна енергія частинки, 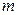 – маса частинки.
– маса частинки.
Для ансамблю розглядуваних частинок теорема Ліувілля виконується.
11.7.Розв’язання аналогічне розв’язанню задачі 11 цього розділу. Теорема Ліувілля не виконується. Це зрозуміло, адже розглядувані системи ансамблю є неконсервативними.
11.8.Для ансамблю електронів, що рухаються в магнітному полі, теорема Ліувілля виконується.
11.9.Для класичної частинки 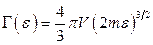 .
.
Для релятивістської частинки 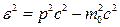 і
і 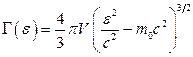 .
.
Розділ 12. Загальні методи рівноважної класичної статистики
12.1. Інтегрувальним множником для 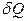 є
є 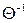 :
: 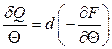 .
.
12.4. а) 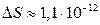 Дж/К; б)
Дж/К; б) 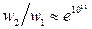 .
.
12.5. 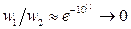 . При
. При 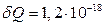 Дж
Дж 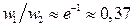 .
.
12.6. 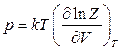 ,
, 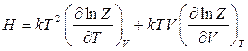 ,
,
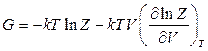 ,
, 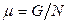 .
.
Розділ 13. Статистична теорія класичних ідеальних систем
13.1. 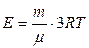 , де
, де  – молярна маса вуглецю. При
– молярна маса вуглецю. При 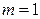 кг
кг 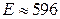 ккал/кг.
ккал/кг.
13.2. 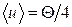 .
.
13.3. 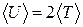 , де
, де 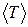 – середня кінетична енергія м’яча.
– середня кінетична енергія м’яча.
13.5. 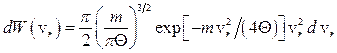 ,
, 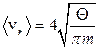 .
.
Середнє значення кута між швидкостями молекул дорівнює 90°.
13.6.Число зіткнень однієї молекули з рештою молекул за одиницю часу
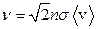 , де
, де 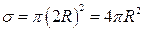 .
.
Середня довжина вільного пробігу молекули 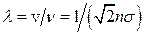 .
.
Середній час вільного пробігу 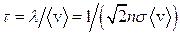 .
.
13.7. Щільність імовірності розташування диполя під кутом 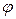 до зовнішнього поля
до зовнішнього поля
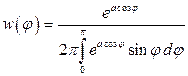 , де
, де 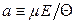 .
.
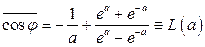 ,
,
де 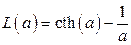 – функція Ланжевена.
– функція Ланжевена.
13.8. 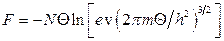 ,
,  ,
, 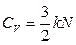 ,
,
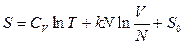 ,
, 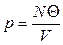 ,
, 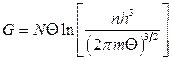 ,
,
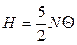 ,
, 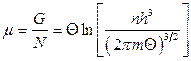 .
.
У наведених формулах 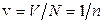 .
.
13.9. 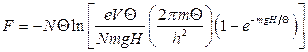 ,
, 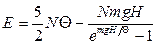 ,
,
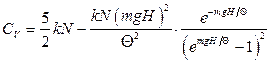 .
.
13.10. 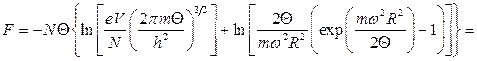
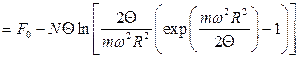 ,
,
де 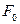 – енергія Гельмгольца при відсутності обертання.
– енергія Гельмгольца при відсутності обертання.
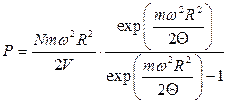 ,
, 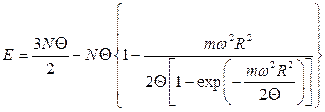 , де
, де 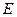 – внутрішня енергія газу у системі відліку, що зв’язана з нерухомим термостатом.
– внутрішня енергія газу у системі відліку, що зв’язана з нерухомим термостатом.
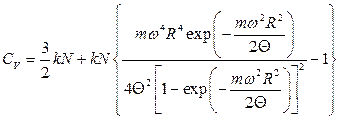 .
.
Розділ 14. Основи квантової статистики
14.1. 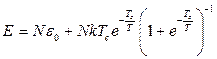 , де
, де 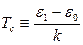 .
.
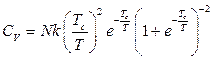 .
.
14.2. 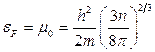 .
.
14.4. 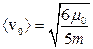 , де
, де 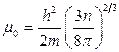 .
. 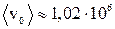 м/с.
м/с.
14.5.  , де
, де 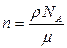 – концентрація атомів у кристалі (вона наближено дорівнює концентрації електронів у металі;
– концентрація атомів у кристалі (вона наближено дорівнює концентрації електронів у металі;  – густина міді;
– густина міді;  – її молярна маса);
– її молярна маса); 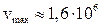 м/с.
м/с.
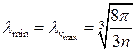 ,
, 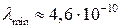 м.
м.
14.6. 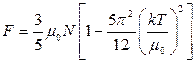 ,
, 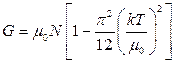 ,
, 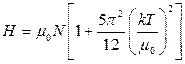 .
.
14.7. 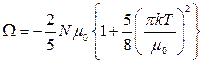 ,
, 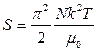 .
.
14.8. 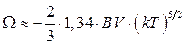 ,
, 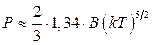 ,
,
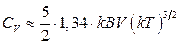 ,
, 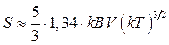 .
.
У наведених формулах 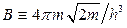 ,
, 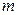 – маса бозе-частинки.
– маса бозе-частинки.
14.9. 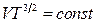 або
або 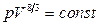 .
.
Розділ 15. Осцилятор і ротатор у термостаті
15.1. 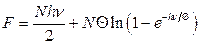 ,
, 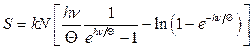 .
.
15.2. 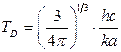 ,
, 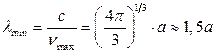 .
.
15.3. 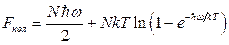 ,
, 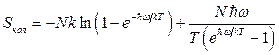 .
.
15.4. 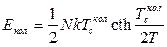 ,
, 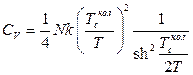 , де
, де 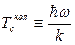 .
.
а) при 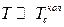 маємо
маємо 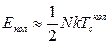 ,
, 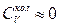 .
.
б) при 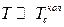 маємо
маємо 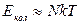 ,
, 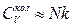 .
.
15.5. 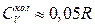 .
.
15.6. 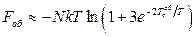 ,
, 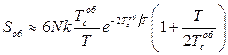 , де
, де 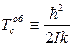 .
.
15.7. 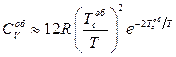 ,
, 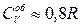 .
.
15.8. Для параводню 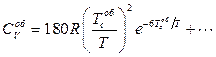 ,
, 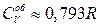 .
.
Для ортоводню 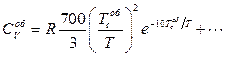 ,
, 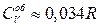 .
.
15.9. 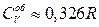 .
.
Розділ 16. Статистична теорія рівноважного випромінювання
16.2. 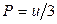 , де
, де 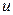 – густина енергії випромінювання.
– густина енергії випромінювання.
16.3. 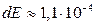 Дж.
Дж.
16.5. 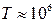 К.
К.
16.6. 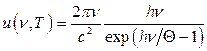 ,
, 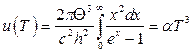 ,
,
де 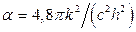 .
.
Розділ 17. Елементи теорії флуктуацій
17.1. 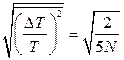 ,
, 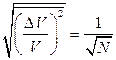 . Згідно з даними умови задачі отримуємо, що відносна флуктуація температури
. Згідно з даними умови задачі отримуємо, що відносна флуктуація температури 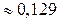 , а відносна флуктуація об’єму
, а відносна флуктуація об’єму 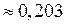 .
.
17.2. Абсолютна флуктуація числа частинок 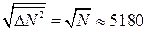 . Відносна флуктуація
. Відносна флуктуація 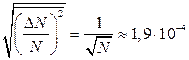 .
.
17.3. 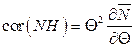 .
.
17.4. 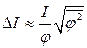 .
.
17.5. 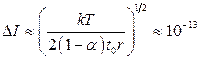 А.
А.
17.6. 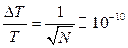 .
.
17.7. 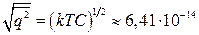 Кл.
Кл.
17.8. 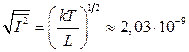 А.
А.
17.9. 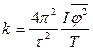 .
.
Список рекомендованої літератури
1. Федорченко А.М. Теоретична фізика: Підручник: У 2 т. Т 2. Квантова механіка, термодинаміка і статистична фізика. – К.: Вища шк., 1993. – 415 с.
2. Венгер Є.Ф. та ін. Основи статистичної фізики і термодинаміки / Є.Ф. Венгер, В.М. Грибань, О.В. Мельничук. – К.: Вища шк., 2004. – 255 с.
3. Базаров И.П. Термодинамика. – М.: Высш. шк., 1991. – 376 с.
4. Базаров И.П., Геворкян Э.В., Николаев П.Н. Задачи по термодинамике и статистической физике. – М.: Высш. шк., 1996. – 352 с.
5. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: В 10 т. Т. V. Статистическая физика. – М.: Наука, 1976. – 584 с.
6. Леонтович М.А. Введение в термодинамику. Статистическая физика. – М.: Наука, 1983. – 416 с.
7. Осипов О.Ю. Термодинаміка в прикладах і задачах. – Запоріжжя, Запорізький державний університет, 2004. – 115 с.
8. Осипов О.Ю. Статистична фізика в задачах. – Запоріжжя: Запорізький національний університет, 2008. – 98 с.
9. Серова Ф.Г., Янкина А.А. Сборник задач по термодинамике. – М.: Просвещение, 1976. – 160 с.
10. Сычев В.В. Дифференциальные уравнения термодинамики. – М.: Высш. шк., 1991. – 224 с.
11. Шиллинг Г. Статистическая физика. Пер. с нем. Под ред. Д.Н. Зубарева и Э.Л. Нагаева. – М.: Мир, 1976. – 432 с.
Зміст
Передмова …………………………………………………………….………… 3
Частина перша. ТЕРМОДИНАМІКА…………………. 4
Розділ 0. Основні поняття і вихідні положення термодинаміки……..… 4
Розділ 1. Математичний апарат термодинаміки………………………… 11
1.1. Теоретичні відомості …………………………………........……… 11
1.2. Приклади характерних задач з розв’язанням …...………….…… 14
1.3. Задачі для самостійного розв’язування ………………..………… 17
Розділ 2. Перше начало термодинаміки……………………..……….…… 19
2.1. Теоретичні відомості ………………………………...……….…… 19
2.2. Приклади характерних задач з розв’язанням …………….……… 22
2.3. Задачі для самостійного розв’язування …………….…….……… 27
Розділ 3. Друге начало термодинаміки…………………………….……… 29
3.1. Теоретичні відомості ……………………………..…….…………. 29
3.2. Приклади характерних задач з розв’язанням ………….………… 34
3.3. Задачі для самостійного розв’язування ………….…….………… 40
Розділ 4. Коефіцієнт корисної дії (ККД) циклів. Цикл Карно…….…… 41
4.1. Теоретичні відомості ………………………………………..……. 41
4.2. Приклади характерних задач з розв’язанням ……………...……. 42
4.3. Задачі для самостійного розв’язування ……………………..…… 51
Розділ 5. Метод термодинамічних потенціалів………………..….……… 53
5.1. Теоретичні відомості ……………………………………....……… 53
5.2. Приклади характерних задач з розв’язанням …………….....…… 57
5.3. Задачі для самостійного розв’язування ………………….…….… 64
Розділ 6. Складні системи і системи зі змінним числом частинок.…… 67
6.1. Теоретичні відомості ………………………………………….….. 67
6.2. Приклади характерних задач з розв’язанням .……………...…… 70
6.3. Задачі для самостійного розв’язування ………………….……… 74
Розділ 7. Третє начало термодинаміки……………………...….………… 75
7.1. Теоретичні відомості …………………………….…….…………. 75
7.2. Приклади характерних задач з розв’язанням ..…….….………… 76
7.3. Задачі для самостійного розв’язування ………………….……… 78
