Формулировка второго начала термодинамики
Первое начало термодинамики дает точный количественный критерий для расчета превращений энергии в любых процессах, но оно ничего не говорит о направлении этих процессов.Практически все они являются необратимыми и в простых случаях нетрудно предсказать их направление на основании «здравого смысла» Так, тепло обычно переходит от теплого тела к холодному, а при движении с трением механическая энергия превращается в тепловую. Однако «здравый смысл» может привести к совершенно неправильным выводам, когда изучаемые процессы выходят за рамки нашего повседневного опыта.
В биофизике и биохимии часто трудно предвидеть, как будет происходить то или иное явление в интересующих нас условиях. Поэтому необходим алгоритм, который давал бы возможность достоверно предсказывать направление процессов в любом случае, независимо от степени наглядности исследуемого явления. Термодинамика позволяет сформулировать такой алгоритм — он получил название второго начала термодинамики.
Проще всего оно формулируется для изолированных систем: в изолированной системе общее изменение энтропии всегда положительно. Нужно подчеркнуть, что речь идет именно об общем изменении энтропии системы. В той или иной части системы энтропия может и уменьшиться, но это уменьшение обязательно перекрывается возрастанием энтропии в других частях системы.
Рассмотрим простой пример Пусть изолированная система состоит из двух тел «1» и «2», обладающих неодинаковой температурой (T1 >T2) Тело «1» отдаст некоторое количество тепла Q, а второе тело его получит (так как система изолированная, то никаких потерь тепла нет) Изменение энтропии первого тела составит
Δs1 =-(Q/T1) (его энтропия уменьшается),
а энтропия второго тела увеличивается на Δs2= + (Q/T2)
Общее изменение энтропии
Δsобщ = Δs1 + Δs2 = -(Q/T1) + (Q/T2)
Так какT2<T1, то выражение в скобках положительно и Δsобщ >0 Такой процесс соответствует второму началу термодинамики и, следовательно, происходит самопроизвольно
Если бы тепло переходило от холодного тела к нагретому, то As данного процесса должно иметь отрицательное значение Подобное событие характеризуется ничтожной вероятностью и практически никогда не происходит.
ДИССИПАТИВНАЯ ФУНКЦИЯ
Изменение энтропии системы можно выразить через обобщенные силы и обобщенные координаты, характеризующие эту систему:
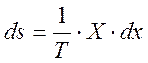
Отсюда можно найти скорость изменения энтропии (ds/dt). Эту величину называют диссипативной функцией:
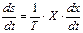
Например, при действии силы трения диссипативная функция выражается так:
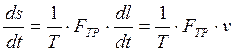
Если в системе идет химическая реакция, то обобщенной силой является химический потенциал (μx ), а обобщенной координатой— число молей вещества, вступающих в реакцию (v). Диссипативная функция имеет вид:
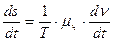
где dν/dt скорость реакции.
Если в системе происходит несколько процессов, то ее диссипативная функция определяется по формуле:
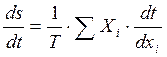
Диссипативную функцию, рассчитанную на единицу объема (V), называют удельной продукцией энтропии:
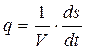
Ее можно считать количественной мерой необратимости процесса: чем больше q3, тем процесс дальше от обратимого.
Важным примером диссипации энергии является демпфирование. Этим термином обозначают уменьшение величины действующей силы (и, соответственно, ускорения) за счет перехода механической энергии в тепловую. В организме человека и животных демпфирующими свойствами обладают скелетные мышцы, связочный аппарат, система кровообращения и др. Демпфирование играет важную роль в ослаблении нагрузок, действующих на организм. Это активный процесс, регулируемый центральной нервной системой. Выработка навыков демпфирования необходима летчикам, космонавтам, парашютистам, горнолыжникам — всем, кому приходится испытывать перегрузки. Следовательно, диссипация энергии не всегда должна рассматриваться как отрицательное явление. Примером использования диссипации энергии в лечебных целях служит высокочастотная электротерапия (например, УВЧ терапия), когда электромагнитная энергия в тканях организма диссипирует в тепло.
Диссипация энергии происходит во всех самопроизвольных процессах, идущих в изолированных системах. Так, при расширении газа его энтропия возрастает, поскольку с увеличением объема увеличивается число вариантов распределения молекул (растет термодинамическая вероятность). Возрастание энтропии свидетельствует об уменьшении свободной энергии.
Более сложным примером является смешение двух разных веществ. При образовании смеси работа не совершается, и может показаться, будто свободная энергия не изменяется. Однако в смеси веществ число вариантов распределения молекул больше, чем в сумме объемов, занимаемых ими до смешения. Следовательно, для смеси характерны более высокие величины термодинамической вероятности и энтропии. Поэтому вещества довольно легко смешиваются, тогда как обратный процесс (самопроизвольное разделение смеси на компоненты) практически невероятен. Однако за счет подведения энергии извне можно добиться разделения смеси на составляющие ее вещества. Свободная энергия такой системы повышается.
В природе происходит немало процессов, вследствие которых свободная энергия той или иной системы возрастает, но они протекают только при наличии другой системы, «питающей» первую свободной энергией. Естественно, что при сопряжении процессов в двух системах свободная энергия одной из них обязательно понижается, причем общее изменение свободной энергии в полной системе, состоящей из нескольких взаимодействующих частей, всегда отрицательно, то есть ее энергия непременно претерпевает диссипацию.
Важную роль в процессах жизнедеятельности играет сопряжение электронных переходов в биологически важных молекулах с изменением их конформации (электронно-конформацион-ное взаимодействие — ЭКВ). Во многих процессах молекулы биополимеров (в первую очередь белков) так меняют свою третичную структуру, что их свободная энергия заметно возрастает. Этот запас свободной энергии может затем использоваться для совершения работы. Грубо говоря, молекула «работает» наподобие пружины: сжимается и разжимается. Подобное явление лежит в основе мышечного сокращения; так действуют многие ферменты. ЭКВ может происходить потому, что оно сопряжено с перестройкой электронной оболочки молекулы, то есть с переходом электронов на другие энергетические уровни, что приводит к освобождению заключенной в них энергии. Часть последней обеспечивает возрастание свободной энергии молекулы, испытавшей конформационную перестройку, а часть — диссипирует. Общее же изменение свободной энергии оказывается отрицательным в соответствии со вторым началом термодинамики, Сопряжение термодинамических процессов широко распространено в биологических системах.
