Первый закон термодинамики. Внутренняя энергия системы включает в себя:

Внутренняя энергия

Внутренняя энергия системы включает в себя:

ü кинетическую энергию поступательного, вращательного и колебательного движения частиц;

ü потенциальную энергию взаимодействия частиц (их притяжение или отталкивание);

ü энергию электронных оболочек атомов;

ü внутриядерную энергию.

В большинстве теплоэнергетических процессов две последние составляющие остаются неизменными. Поэтому в дальнейшем под внутренней энергией будем понимать энергию хаотического движения молекул, внутримолекулярную энергию и потенциальную энергию сил взаимодействия между молекулами.

Кинетическая энергия молекул является функцией температуры, значение потенциальной энергии зависит от среднего расстояния между молекулами и, следовательно, от занимаемого газом объема V, т. е. является функцией V. Следовательно, внутренняя энергия U есть функция состояния тела, т.е. зависит только от его параметров.

Величина u = U / M, называется удельной внутренней энергией (Дж/кг), представляет собой внутреннюю энергию единицы массы вещества.

В дальнейшем для краткости будем называть величину u просто внутренней энергией. Поскольку внутренняя энергия есть функция состояния тела, то она может быть представлена в виде функции двух любых независимых параметров, определяющих это состояние:

u = φ₁(p, v); u = φ₂(p, T); u = φ₃(v, T).

Ее изменение в термодинамическом процессе ∆u не зависит от характера процесса и определяется только начальным и конечным состояниями тела: ∆u= 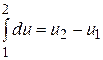, где u₁ – значение внутренней энергии в начальном состоянии, а u₂ – в конечном. Математически это означает, что бесконечно малое изменение внутренней энергии du есть полный дифференциал u; если выразить внутреннюю энергию в виде функции удельного объема и температуры, то

du = (∂u/∂T)_vdT + (∂u /∂v)_Tdv. (2.1)

Для подзабывших математику напомним. Если какая-либо величина у зависит только от одной переменной y=f(x), то скорость ее изменения характеризуется производной 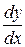. Бесконечно малое изменение функции dy 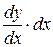называется дифференциалом.

Если же величина у зависит от двух аргументов 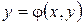, то для оценки изменения у необходимо учитывать изменение их обоих. В этом случае вводят частные производные, т.е. 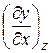и 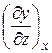. Первая характеризует скорость изменения у при изменении х, но при постоянном значении z; вторая – скорость изменения у при изменении z, но постоянном значении х. Полное изменение функции при изменении х на dx и z на dz будет равно 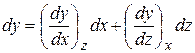. Величина dy в этом случае называется полным дифференциалом.

Внутренняя энергия идеального газа, в котором отсутствуют силы взаимодействия между молекулами, не зависит от объема газа или давления [(∂u / ∂v)_T = 0, (∂u / ∂р)_Т = 0], а определяется только его температурой, поэтому производная от внутренней энергии идеального газа по температуре есть полная производная:

(∂u / ∂T)_р = (∂u / ∂T)_v = du/dT. (2.2)

Для задач технической термодинамики важно не абсолютное значение внутренней энергии, а ее изменение в различных термодинамических процессах. Поэтому начало отсчета внутренней энергии может быть выбрано произвольно. В соответствии с международным соглашением для идеальных газов за нуль принимается значение внутренней энергии при температуре 0 °С вне зависимости от давления.