Обработка результатов измерений. 1. На основании формулы (14) для каждого значения UR рассчитать соответствующее ему значение I , а затем из (13) определить величину сопротивления проволоки

1. На основании формулы (14) для каждого значения U_R рассчитать соответствующее ему значение I , а затем из (13) определить величину сопротивления проволоки R₂. Полученные опытные данные записать в таблицу.

2. Из формулы (9) найти значение Т₂, рассчитать Т₂ - Т₁, результат занести в таблицу.

3. Используя формулу Р = I U_П, рассчитать мощность, выделяемую при прохождении электрического тока I по вольфрамовой проволоке для каждого его значения. Записать результат в таблицу.

4. Рассчитать величину l для каждого значения Т₂ и сравнить с табличными значениями с учетом погрешности измерения.

5. Построить график зависимости l=l (Т₂).

6. Показать, что при данных условиях эксперимента энергия излучения W_изл составляет несколько процентов от энергии Р, выделяемой текущим по проволоке током. Для этого рассчитать W_изл вольфрамовой проволоки по формуле (12) и сравнить со значениями Р.

Контрольные вопросы

1. Что такое теплопроводность? Объяснить это явление на основании положений молекулярно-кинетической теории.

2. Записать закон Фурье для теплопроводности и дать его формулировку.

3. Определить физический смысл градиента температуры?

4. Какой физический смысл имеет коэффициент теплопроводности? От чего он зависит?

5. Что такое поток тепла, куда он направлен?

6. Что такое явление переноса? Какие явления переноса вы знаете.

7. Выведите рабочую формулу (7). Что необходимо знать, чтобы рассчитать коэффициент теплопроводности?

8. Как рассчитываются в данной работе температура, сопротивление и мощность, выделяемая на вольфрамовой проволоке при изменении тока в цепи? Как зависит сопротивление проволоки от температуры?

9. Указать источники погрешностей измерений.

10. Запишите и сформулируйте закон Стефана – Больцмана

11. Какая энергия теряется на излучение?

12. Как определяется понятие температуры в молекулярно-кинетической теории?

Лабораторная работа № 2

ИЗМЕРЕНИЕ УДЕЛЬНОЙ ТЕПЛОЁМКОСТИ ВОЗДУХА

ПРИ ПОСТОЯННОМ ДАВЛЕНИИ

Цель работы:экспериментальное определение теплоёмкости воздуха при постоянном давлении методом протока; изучение методов измерения разности температур и расхода воздуха.

Введение

Понятие внутренней энергии тела включает в себя кинетическую энергию движения молекул, кинетическую энергию движения атомов внутри молекул, кинетическую энергию частиц, входящих в состав атомов, потенциальную энергию взаимодействия молекул между собой и атомов внутри молекул. Для идеального газа отсутствует взаимодействие молекул между собой и его внутренняя энергия будет полностью определяться кинетической энергией всех видов движения, в которых может участвовать молекула.

Кинетическая энергия одноатомной молекулы идеального газа определяется выражением:

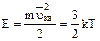(1)

где k = 1,38×10 ^-23 Дж / К - постоянная Больцмана, 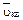- средняя квадратичная скорость молекулы, m- масса молекулы, T - температура газа.

По теореме Больцмана при тепловом равновесии для данной температуры Т средняя кинетическая энергия молекул равномерно распределена между степенями свободы молекулы и для каждой степени свободы равна .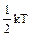

Под числом степеней свободы подразумевается число независимых координат, которое нужно ввести для полного определения положения тела в пространстве. Положение одноатомной молекулы в декартовой системе координат определяется тремя координатами, т.е. молекула имеет три поступательные степени свободы.

Двухатомную молекулу обычно представляют в форме гантели (жесткая связь), центр которой совпадает с началом координат. Такая молекула может двигаться поступательно как целое в трех взаимно перпендикулярных направлениях. Кроме того, молекула может вращаться вокруг этих же осей, причем вращение вокруг оси, проходящей по линии соединяющей атомы, не изменяет положения системы в пространстве и лишено смысла. Таким образом, для определения положения двухатомной молекулы в пространстве необходимо задать пять степеней свободы (три поступательные и две вращательные). Трехатомная нелинейная молекула, а также любая многоатомная молекула имеет шесть степеней свободы - три поступательных и три вращательных.

Естественно, что жесткой связи между атомами не существует. Поэтому при распределении энергии необходимо учитывать и колебательные степени свободы. Было показано, что двухатомная молекула имеет одну колебательную степень свободы, трехатомная - три, четырехатомная - шесть. Общее число степеней свободы (поступательные, вращательные и колебательные) в n - атомной молекуле равно i = 3n.

Закон распределения энергииимеет место и для вращательных, и колебательных степеней свободы. На каждую вращательную степень свободы также приходится энергия 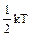. Если амплитуда колебаний мала по сравнению с расстояниями между атомами, то колебания можно считать гармоническими. На каждую колебательную степень свободы приходится энергия равная kT ( 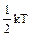в виде кинетической и 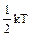-потенциальной энергии).

Следовательно, среднее значение энергии молекулы равно:

= ,

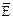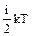где i = i _п+ i_вр + 2i _кол , i_п, i _вр, i _кол - число поступательных, вращательных и колебательных степеней свободы соответственно.

Внутренняя энергия одного моля газа:

U_μ = N_A = ,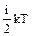

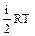где N_А - число Авогадро, R = 8,31 Дж/( моль×К) - универсальная газовая постоянная. Таким образом, внутренняя энергия определяется числом степеней свободы и температурой газа и не зависит от его объема.

Изменение внутренней энергии системы может быть осуществлено двумя путями:

1) путем передачи системе (или от системы) некоторого количества теплоты dQ;

2) путем совершения системой работы против внешних сил (или совершения внешними силами работы над системой).

Закон сохранения энергии в этом случае формулируется следующим образом: переданное системе количество теплоты dQ идет на изменение внутренней энергии системы dU и на совершаемую системой работу dA (I закон термодинамики или первое начало термодинамики):

dQ = dU + dA (1)

Теплоемкостью тела C называют величину, равную количеству теплоты dQ, которую нужно сообщить телу (отнять от тела), чтобы изменит его температуруT на 1K:

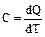
Теплоемкость единицы массы вещества называется удельной теплоемкостью 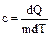. Ее размерность - [Дж/(кг×К)].

Теплоемкость одного моля вещества называется молярной теплоемкостью С _{m.= 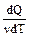.} Ее размерность - [Дж/(моль×К)].

Удельная и молярная теплоемкости связаны соотношением:

,

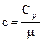где m - молярная масса вещества.

Найдем теплоемкости газа при различных условиях:

1) при постоянном объёме;

2) при постоянном давлении.

1. Изохорный процесс для одного моля вещества(V=const, m=m).

В этом случае работа, совершаемая газом при нагревании:

dA = pdV = 0

и первый закон термодинамики запишется в виде:

dQ =dU,

т.е. все количество теплоты, переданное газу, идет на увеличение его внутренней энергии. Тогда получаем для теплоемкости при V=const:

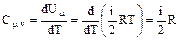(2)

2. Изобарный процесс для одного моля вещества( m=m, р=const).

В данном случае количество теплоты, переданное газу, идет на увеличение его внутренней энергии и на совершение им работы против внешних сил:

dQ=dU_µ+pdV_µ.

Из уравнения состояния следует, что рdV= 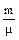RdT и для одного моля:

рdV_μ=RdT,

тогда имеем:

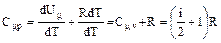(3)