Вимірювання фізичних величин

Виміряти будь-яку величину-це означає дізнатися у скільки разів в цій величині вміщується однорідна з нею величина, прийнята за одиницю вимірювання. Необхідно завжди враховувати, що неможливо здійснити ніяких вимірювань абсолютно точно. В результаті будь-якого вимірювання, яким-завгодно приладом, отримується лише наближене значення дійсної величини, яке має в собі помилки, обумовлені неточністю методики експерименту, недостатньою чутливістю приладів, а також недосконалістю наших органів чуттів.

Відхилення вимірювань величини Хі від її істинного значення Х називається помилкою вимірювання Х=Хі-Х. Помилки вимірювань поділяються на систематичні та випадкові. Крім того, бувають і грубі помилки (промахи), викликані якимось неврахуванням при постановці та проведені експерименту, наприклад, невірний відлік або помилковий запис показань приладу. Систематичною називається помилка, яка залишається постійною протягом всієї серії вимірювань. Систематична помилка, як правило, є наслідком:

1. Несправності приладів, неточної установки нуля приладу, неправильного вибору шкали приладу або відліку.

2. Помилок, допущених в процесі вимірювань.

3. Однобічного впливу зовнішніх умов на показання приладів (вплив тиску, температури або градієнта температур і т.д.).

Так як систематичні помилки повторюються протягом всієї серії вимірювань, то вони входять в середнє арифметичне значення вимірюваної величини. Для ліквідації систематичних помилок потрібно додержуватися методики вимірювань та правил користування вимірювальними приладами.

В експерименті завжди присутні випадкові помилки. Ці помилки обумовлені, головним чином, недосконалістю наших органів чуттів та носять статистичний характер, так як ймовірність отримання при відліку як завищеного, так і заниженого результатів – однакова.

Вплив випадкових помилок на результати експерименту можна проаналізувати за допомогою теореми похибок. При відсутності систематичних помилок, випадкові помилки є причиною розбіжності повторних вимірювань відносно істинного значення. Однак, якщо крім випадкових помилок є і систематична, то результати вимірювань будуть розкидані відносно не дійсного, а зміщеного значення.

Розглянемо в якості прикладу №1, вимірювання секундоміром періоду коливання маятника. Похибки моменту запуску і зупинки секундоміра, помилка у величині відліку, невелика нерівномірність руху маятника – все це викликає розбіжності результатів повторних вимірювань і тому призводить до випадкових помилок.

Якщо помилки носять тільки випадковий характер, то одні результати вимірювань періоду коливання маятника будуть дещо завищеними, а другі – дещо заниженими. Але якщо секундомір ще й поспішає або відстає, то всі результати, відповідно, будуть занижені або завищені.

Дійсно, що деякі фактори можуть викликати одночасно і систематичні, і випадкові помилки. Так, вмикаючи і вимикаючи секундомір, можна створити малу нерегулярну розбіжність моментів запуску і зупинки секундоміра відносно руху маятника, і внести тим самим випадкову помилку. Але якщо, до того , кожен раз поспішають, включаючи секундомір, або дещо запізнюються, вимикаючи його, або те і друге разом, то це призведе до систематичної помилки.

На другому прикладі, використання найпростішого прикладу – вимірювальної лінійки, можна викласти деякі загальні пункти, якими потрібно керуватися під час проведення вимірювань.

Приклад №2. Визначення лінійних розмірів тіл при допомозі вимірювальної лінійки. Вимірювальна лінійка є найпоширенішим вимірювальним приладом, внаслідок простоти виготовлення та користування. Лінійка дозволяє отримати результати з точністю до 0.2 мм, однак для цього при вимірюванні потрібно уникати певних помилок:

а). Помилка обумовлена паралаксом.

а б

дзеркало

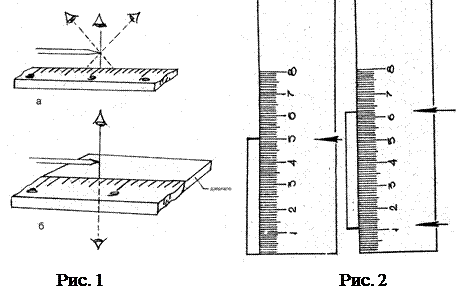Якщо вимірюваний предмет знаходиться на деякій відстані від шкали і якщо ми дивимось не під прямим кутом до шкали, то відлік буде неправильним (рис.1а). Потрібно відмітити, що така помилка можлива під час користування приладом із стрілкою, яка рухається по шкалі і називається помилкою паралакса. Цю помилку можна зменшити, наближаючи до шкали вимірюваний предмет або стрілку, а також використовуючи дзеркало розміщене біля шкали (рис. 1б). Потрібно, щоб зображення предмета збіглося б з його відображенням у дзеркалі, тоді забезпечується прямий кут між лінією зору та шкалою.

б). Помилка відліку нуля.

Зазвичай, при вимірюваннях розміщують лінійку так, щоб її край співпав з одним кінцем предмету, і відраховують показання з другого кінця (рис. 2а). Такий спосіб вимірювання годиться тільки для грубих вимірювань довжини, так як, край лінійки може бути зіпсованим або нульова відмітка поставлена невірно. Тому вимірюваний предмет потрібно розміщати таким чином (рис. 2б), щоб можна було знімати показання з обох кінців.

Взагалі-то, завжди у будь-якому приладі, потрібно з деякою підозрою ставитися до нульової поділки шкали. Подібної помилки можна уникнути, якщо брати різницю двох відрахунків.

в). Калібрування.

Шкала на лінійці може бути нанесена неправильно. Тому лінійку потрібно перевірити, або відкалібрувати. Зробити це можна, якщо суміщати дану лінійку з більш точною лінійкою та порівнюючи їх показання. Якщо в ході експерименту потрібна певна ділянка лінійки, то можна відкалібрувати тільки цю ділянку.

Принцип калібрування широко використовується при будь-яких вимірюваннях. Калібрувати можна будь-які вимірювальні прилади та особливо ретельно це потрібно робити в тому діапазоні, де цей прилад використовується.

2. Визначення помилки вимірювань

При вимірюванні фізичної величини можливі два випадки. У першому випадку, вимірювана фізична величина визначається прямим вимірюванням за допомогою певного приладу (наприклад: лінійні розміри, вага, температура і т.д.).

У другому випадку, і цей випадок характерний для більшості лабораторних робіт, при визначенні фізичної величини потрібно провести прямі вимірювання декількох інших величин, а потім по формулах вирахувати потрібну величину.

Кожна із величин, які входять до формули, виміряна з певною точністю і впливає на точність кінцевого результату. Такі вимірювання називаються непрямими.

Відповідно і помилки вимірювань поділяються на помилки при прямих вимірюваннях та помилки при непрямих вимірюваннях.

2.1. Визначення помилки при прямих вимірюваннях

Якщо величина Х виміряна n разів в однакових умовах, то при цьому ми отримаємо ряд близьких значень величини Хі. Різні значення величини Хі пояснюються тим, що при її вимірюваннях були допущені випадкові помилки. Так як випадкові помилки, як це вказувалось, носять статистичний характер(тобто відхилення в більшу і меншу сторону рівновірогідні), тобто найбільш близьким до істинного значення вимірюваної величини, буде середнє арифметичне результатів всіх вимірювань, виключаючи грубі помилки:

.

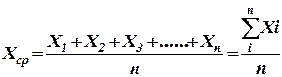Очевидно, що чим більше буде виконано вимірювань, тим точніше буде співпадати середнє арифметичне значення з істинним значенням даної величини. Так як істинне значення Х вимірюваної величини в багатьох випадках невідомо, то за цю величину приймається середнє арифметичне результатів окремих вимірювань. За абсолютну помилку окремих вимірювань приймається різниця між виміряним значенням величини та їх середнє арифметичним значенням.

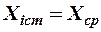
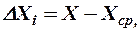
Вирахувана таким чином сума помилок, рівна нулю з точністю до округлення середнього арифметичного. Тому за середню абсолютну помилку вимірювання приймається величина, яка рівна середньому арифметичному значенню із абсолютних величин всіх помилок вимірювань, тобто:

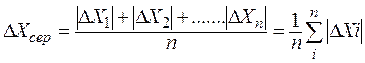
Згідно теорії вірогідності, дійсне значення величини Х буде лежати в межах Х_сер±DХ_сер з вірогідністю 64%, при числі вимірювань менше 4. Якщо число вимірювань n=4, то вірогідність співпадання Х_сер±DХ_сер з істинним значенням дорівнює 90%, а при n=9 ця вірогідність зростає до 98%.

Значення абсолютної помилки дозволяє вказати границі, в яких з визначеною вірогідністю лежить шукана величина.

Кінцевий результат прямого вимірювання фізичної величини записується у вигляді

.

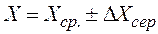Відношення середньої абсолютної помилки вимірювань до значення дійсної величини називається відносною помилкою вимірювання Е, яка виражається у відсотках

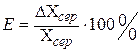
Відносна помилка дозволяє оцінити ступінь точності отриманого результату і показує величину помилки (у відсотках), допущеної при вимірюванні.

Очевидно, що середнє арифметичне значення шуканої величини Хсер, потрібно округляти до того розряду, що і абсолютну помилку, а відносна помилка завжди вираховується не менше ніж з двома означаючими цифрами.

В деяких випадках неможливо повторити пряме вимірювання дійсної величини декілька раз. Тоді вимірювання проводять тільки один раз, а абсолютну помилку визначають або по класу точності приладу, або приймаючи за абсолютну помилку половину ціни найменшої поділки шкали приладу, так як при вимірюваннях не можна помилитися більш, ніж на половину поділки.

На кінець відмітимо, що якщо помилка, визначена по середньому значенню, менша, ніж помилка визначена по класу точності, або ціні найменшої поділки, то за абсолютну помилку в цьому випадку приймається помилка, рівна найбільшій із цих трьох величин.

Класом точності приладу називається виражене у відсотках відношення максимальної абсолютної похибки приладу до верхньої границі його вимірювань:

;

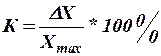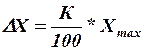
2.2. Визначення помилки при непрямих вимірюваннях

Якщо відкинути грубі помилки, то при багаторазовому повторюванні експерименту в абсолютно однакових умовах, різні значення окремих вимірюваних величин, які входять у формулу, з якої розраховується потрібна фізична величина, отримуються виключно за рахунок похибок вимірювань. Тому в цих випадках в робочу формулу вводять середнє значення вимірюваних величин а помилку вираховують способом диференціювання.

Розглянемо випадок коли деяка величина А являється функцією тільки однієї величини Х:

.

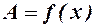Так як майже у всіх випадках помилка вимірювань набагато менша результату вимірювання, то її квадратом можна знехтувати і розглядати абсолютну похибку, як безкінечно малу величину ( 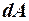замість 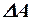та 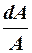замість )

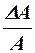З курсу математичного аналізу відомо, що диференціал функції рівний добуткові похідної функції на диференціал її аргументу.

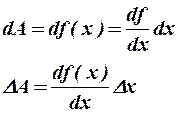
А значить, для визначення абсолютної похибки шуканої величини, яка є функцією вимірюваної величини, потрібно взяти диференціал цієї функції, рахуючи вимірювану величину змінною, і в отриманий вираз, підставити числове значення вимірюваної величини, а замість диференціала аргументу підставити його абсолютну помилку.

Відносна похибка функції А буде:

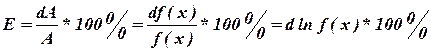
Таким чином, для визначення відносної помилки потрібно взяти диференціал функції, по якій визначається шукана величина, і в отриманий вираз підставити числове значення вимірюваної величини та абсолютної похибки, допущеної при її вимірюванні.

Очевидно, що за формулами, які отримані диференціюванням, обчислюють тільки одну із помилок ( відносну або абсолютну), а другу знаходять із відношень:

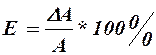або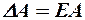

Якщо шукана величина є функцією декількох вимірюваних величин 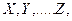які визначені з абсолютними помилками або 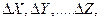то для визначення абсолютної похибки шуканої величини потрібно, як і в попередньому випадку, тільки з однією вимірюваною величиною, знайти диференціал цієї функції, рахуючи всі вимірювані величини змінними.

Щоб знайти диференціал функції декількох змінних, потрібно продиференціювати цю функцію по кожній із змінних окремо, рахуючи в кожному випадку змінною ту величину по якій проводиться диференціювання, а інші рахувати сталими, а потім скласти всі окремі диференціали.

Так як окремі диференціали в залежності від виду функції можуть бути позитивними або негативними, то для отримання максимального значення абсолютної похибки, потрібно складати абсолютні значення окремих диференціалів:

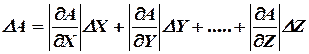
Тому, для визначення відносної похибки функції потрібно взяти диференціал натурального логарифма цієї функції по кожному із аргументів окремо, і додати абсолютні значення добутків окремих похідних на помилку аргументу:

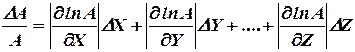
Відмітимо два окремих випадки , які мають великий практичний інтерес:

1. Якщо шукана величина 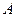рівна сумі або різниці вимірюваних величин 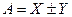, то у відповідності з правилами диференціювання функції декількох змінних , отримаємо, що помилка шуканої величини рівна сумі абсолютних помилок вимірюваних величин, тобто

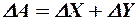
В цьому випадку вимірювання 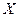та 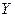потрібно проводити з однаковою абсолютною похибкою 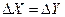, та всі три величини округлити до однакового розряду.

1. Якщо, шукана величина 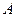рівна добутку або частці від виміряних величин, то відносна помилка 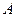рівна сумі відносних виміряних величин:

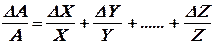
В цьому випадку вимірювання всіх величин потрібно проводити з однаковою кількістю значущих цифр.