Вопрос 11. Адиабатный и политропный процессы. Уравнение Пуассона

Адиабатным называется процесс, при котором отсутствует теплообмен ( 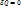) между системой и окружающей средой.

Выведем уравнение адиабаты:

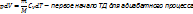
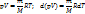
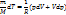
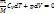
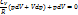
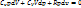
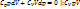
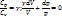
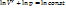
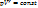
При адиабатном процессе работа совершается только за счёт убыли внутренней энергии. При расширении газа работа «+». Связь между давлением и объёмом в адиабатном процессе:

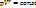
Если

В современной технике адиабатические процессы имеют очень большое значение, для получения сверхнизких/сверхвысоких температур. Адиабатные процессы проводят или очень быстро или осуществляют их в теплоизоляционных оболочках.

Политропный процесс – процесс, проходящий с постоянной теплоемкостью.
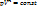- уравнение политропности.

n=0, p=const
n=1, t=const
n= , =0
n=+- , V=const

Вопрос 24.
Обратимые и необратимые процессы. Круговой процесс (цикл). Термический КПД цикла.
Цикл Карно. КПД цикла Карно.

Обратимые процессы – это идеализация реальных процессов. Термодинамический процесс наз-ся обратимым, если он может происходить как в прямом, так и в обратном направлении и при этом в окружающей среде и самой системе не происходит никаких изменений. Любой процесс неудовлетворяющий этим условиям является необратимым.

Большое значение для применения термодинамики имеют круговые процессы, которые лежат в основе действия всех тепловых машин: холодильников, двигателей, паровых турбин. Тело, совершающее круговой процесс и обменивающееся энергией с др. телами называется рабочим телом. Если тепловая машина преобразовывает теплоту в работу, то это тепловой двигатель, а если посредством работы отнимается теплота у системы, то это холодильник. Круговые процессы изображаются в диаграммах P-V, P-T, V-T в виде замкнутых кривых. Круговой процесс – цикл, потому что за цикл система возвращается в исходное состояние. Если тело получает количество теплоты и совершает работу, то это прямой цикл, а если наоборот, то обратимый.

Чтобы тепловая машина имела возможность совершать работу необходимо наличие холодильника, т.е. тела, которому рабочее тело будет отдавать кол-во теплоты.

а) Q >0 A>0 б) A<0 Q<0

Особое место среди круговых процессов занимает цикл Карно.

Термический КПД – величина, равная отношению работы, совершённой рабочим телом в прямом обратимом цикле, к количеству теплоты, сообщённой в этом процессе нагревателем.

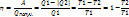
Тепловая машина при данных значениях температуры нагревателя и холодильника не может иметь большего КПД, чем машина, работающая по обратному циклу Карно при тех же значениях температур нагревателя и холодильника.

Цикл Карно является единственным круговым процессом, который, в принципе, можно осуществить обратимым образом.

Адиабатный (∆Q = 0)

Вопрос 15. взаимодействие электрических зарядов. Закон Кулона. Понятие напряженности электрического поля. Напряженность поли точечного заряда. Принцип суперпозиции для электрического поля.

Напряжённость электрического поля - его силовая характеристика.

Напряженность электрического поля - вектор E, который численно равен и совпадает по направлению с силой F, действующей со стороны поля на помещённый в рассматриваемую точку единичный положительный заряд q₀: E=F/ q₀.

Точечный заряд - линейный размер тела, на котором этот заряд сосредоточен, намного меньше любых рассматриваемых расстояний.

Поле точечного заряда - Электрический заряд любого тела состоит из целого числа элементарных зарядов, равных 4,8*10^-10. Электрон - отрицательный - масса 9,1*10^-28г. Протон - положительный - масса 1б67*10^-24г. Напряжённость электрического точечного заряда q равна: E=(1/4pe₀)*(q/er²)*(r/r), где r - радиус-вектор, проведённый из точечного заряда в исследуемую точку поля; e - относительная диэлектрическая проницаемость среды; e₀ - электрическая постоянная. В скалярной форме: E=(q/er²)*(r/r).

Принцип суперпозиции электрических полей - Напряжённость электрического поля системы точечных зарядов равна векторной сумме напряжённостей полей, создаваемых каждым из этих полей в отдельности: E=S_(i=1,n)E_i. *векторная сумма*

Зако́н Куло́на — это закон, описывающий силы взаимодействия между точечными электрическими зарядами.

Был открыт Шарлем Кулоном в 1785 г. Проведя большое количество опытов с металлическими шариками, Шарль Кулон дал такую формулировку закона:

Модуль силы взаимодействия двух точечных зарядов в вакууме прямо пропорционален произведению модулей этих зарядов и обратно пропорционален квадрату расстояния между ними

Иначе: Два точечных заряда в вакууме действуют друг на друга с силами, которые пропорциональны произведению модулей этих зарядов, обратно пропорциональны квадрату расстояния между ними и направлены вдоль прямой, соединяющей эти заряды. Эти силы называются электростатическими (кулоновскими).

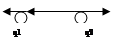
З.Кулона в векторной записи:

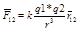
F12= - F21, │F12│= │F21│=F

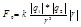
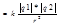
Fо-это сила вз-вия q в вакууме.

Сила эл/ст вз-явия 2 точечных эл.q находящихся в вакууме прямо пропорционален произ-нию абсолютных значений этих q и обратно проп-лен квадрату рас-ния м/у ними.Сила напр-на вдоль соед.прямой.

В среде вз-вие в ε раз меньше.

ε=F0/F – диэлектрич.проницаемость среды, показ-щая во сколько раз сила вз-вия в вакууме больше чем в среде.

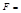
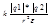
к=1/4πεо,

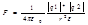
εо-эл.постоянная =8,85*10(-12) (Кл/Н*м²)