Молекулярно-кІнетичної теорії
5.1 Мета роботи
Ознайомитись з основними положеннями молекулярно-кінетичної теорії (МКТ). Переконатись у справедливості основного рівняння МКТ.
5.2 Вказівки з організації самостійної роботи
З точки зору МКТ внаслідок хаотичного руху молекул, газ, який знаходиться в посудині, тисне на її стінки. Тиск, обумовлений тим, що молекули стикаються зі стінками посудини і діють на неї з деякою силою, направленою перпендикулярно до стінки. Вивчення цього процесу базується на двовимірній моделі ідеального газу. Спрощені положення, закладені в цю модель, сформулюємо в такому вигляді:
1. Молекули – пружні кульки малого розміру.
2. Силами взаємодії між молекулами можна знехтувати.
3. Взаємодія між молекулами виникає тільки під час удару між ними, або під час зіткнення молекули зі стінками посудини. Удар під час зіткнень вважаємо абсолютно пружним.
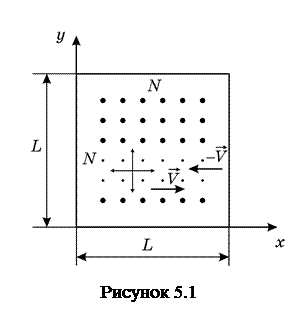 Виведемо рівняння для випадку двовимірного руху молекул. Нехай в квадратній “посудині” з ребром L, яка являє собою контур квадрата (рис. 5.1) перебуває ідеальний газ, молекули якого можуть рухатися в площині x, y в межах 0<x<L, 0<y<L. Кількість молекул дорівнює
Виведемо рівняння для випадку двовимірного руху молекул. Нехай в квадратній “посудині” з ребром L, яка являє собою контур квадрата (рис. 5.1) перебуває ідеальний газ, молекули якого можуть рухатися в площині x, y в межах 0<x<L, 0<y<L. Кількість молекул дорівнює 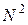 , де N – кількість молекул в напрямку x і в напрямку y (в межах квадрата) однакова. Тоді концентрація молекул на площині квадрата
, де N – кількість молекул в напрямку x і в напрямку y (в межах квадрата) однакова. Тоді концентрація молекул на площині квадрата 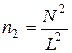 .
.
Припустимо, що кількість молекул, які рухаються в двох взаємно перпендикулярних напрямках до сторін квадрата, дорівнює 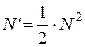 (можливість такого припущення підтверджується чітким розрахунком).
(можливість такого припущення підтверджується чітким розрахунком).
Імпульс сили під час удару молекули об “стінку” дорівнює зміні імпульсу молекули
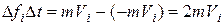 .
.
Очевидно, що імпульс, який отримує “стінка” за 1 секунду від і-ї молекули
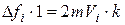 ,
,
де k – кількість ударів і-ї молекули об одну й ту саму (наприклад, праву) стінку за 1 секунду: 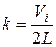 . Тоді
. Тоді
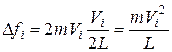 .
.
Враховуючи, що в одному напрямку рухається 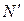 молекул, знайдемо сумарну силу, з якою газ діє на праву стінку
молекул, знайдемо сумарну силу, з якою газ діє на праву стінку
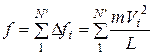 .
.
Розділимо та помножимо праву частину рівняння на 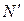
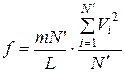 .
.
Величина 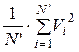 є не що інше, як квадрат середньоквадратичної швидкості
є не що інше, як квадрат середньоквадратичної швидкості 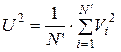 . Тоді
. Тоді 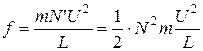 .
.
Розділимо обидві частини останнього рівняння на L, тоді
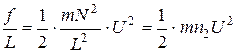 .
.
Очевидно, що 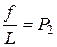 – “тиск” газу на “стінку”, тобто сила, яка діє на одиницю довжини сторони квадрата. Отже,
– “тиск” газу на “стінку”, тобто сила, яка діє на одиницю довжини сторони квадрата. Отже,
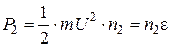 , (5.1)
, (5.1)
де 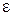 – середня кінетична енергія поступального руху молекули.
– середня кінетична енергія поступального руху молекули.
Аналогічні міркування приводять до закону залежності тиску в тривимірному випадку
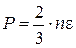 . (5.2)
. (5.2)
Порівнюючи вирази (5.1) та (5.2), можна зробити висновок, що залежність тиску від концентрації молекул і середнього значення енергії залишається однаковою як у двовимірному, так і тривимірному випадку.
Якщо врахувати, що кінетична енергія поступального руху молекули дорівнює 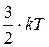 , тобто на одну ступінь свободи доводиться
, тобто на одну ступінь свободи доводиться 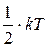 , рівняння (5.2) можна записати у вигляді
, рівняння (5.2) можна записати у вигляді
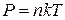 , (5.3)
, (5.3)
а рівняння (5.1) теж матиме такий точно вигляд, бо у двовимірному випадку кількість ступенів свободи дорівнює двом
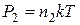 .
.
5.3 Опис комп’ютерної програми
В даній роботі використовується та сама комп’ютерна програма, що і в роботі 4 з тією різницею, що вибирається режим роботи “Визначення тиску”. Зовнішній вигляд інтерфейсу програми зображено на рис. 5.2.
5.4 Інструкція користувачу
1. Встановити режим роботи “Тиск”, ввімкнути “Перегляд”.
2. Встановити значення вихідних параметрів відповідно до табл. 5.1.
3. Обчислити тиск (тривимірна модель), натиснувши кнопку «Старт». Не змінюючи вихідних даних, повторити вимірювання чотири рази. Результати записати в табл. 5.2.
4. Збільшуючи N і M на дві одиниці, отримати залежність тиску P від концентрації молекул n. Для кожного значення концентрації повторювати вимірювання P п’ять разів. Визначити середнє значення 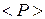 . Результати для семи значень n занести в табл. 5.2.
. Результати для семи значень n занести в табл. 5.2.
Таблиця 5.1 – Вихідні дані
| Номер вар. | ||||||||||||
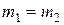 | ||||||||||||
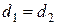 | ||||||||||||
| N | ||||||||||||
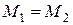 | ||||||||||||
| T |
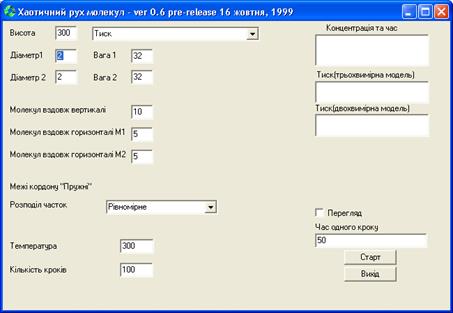
Рисунок 5.2
5. За отриманими даними пунктів 3 і 4 побудувати графік залежності 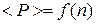 при
при 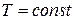 .
.
6. При сталому значенні концентрації n (повернути значення N, M згідно з табл.. (5.1)) виміряти сім значень P, збільшуючи температуру на 100 К. Початкове значення Т взяти з табл. 5.1. При кожному значенні Т повторювати вимірювання тиску P п’ять разів. Визначити середнє значення 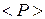 . Результати вимірювань занести в табл. 5.2.
. Результати вимірювань занести в табл. 5.2.
7. За отриманими даними пункту 6 побудувати графік залежності 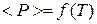 при
при 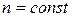 .
.
5.5 Зміст звіту
Звіт має містити: мету роботи, результати вимірювань, зведені в таблиці, похибки вимірювань, графіки залежностей 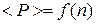 при
при 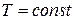 та
та 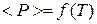 при
при 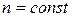 , висновки.
, висновки.
Таблиця 5.2 – Результати розрахунків
| Номер | 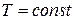 | 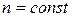 | ||||||||||||||
| n х1024, м-3 | P·103, Па | T | P·103, Па | |||||||||||||
| < P > | D P | < P > | D P | |||||||||||||
5.6 Контрольні запитання і завдання
1. Сформулюйте основні положення моделі ідеального газу.
2. Як в роботі визначається концентрація молекул на площині?
3. Який імпульс отримує стінка посудини під час удару молекули?
4. Як визначається квадрат середньоквадратичної швидкості?
5. Дайте визначення тиску (для двовимірного простору).
6. Порівняйте вирази (5.1) та (5.2). Зробіть висновок, як залежить тиск від величини концентрації та середнього значення енергії молекули.
7. Сформулюйте закон рівнорозподілу (яка енергія припадає на кожний ступінь свободи молекули).
8. Сформулюйте основне рівняння МКТ.
9. Зробіть висновок з порівняння формул (5.4), (5.5).
