Examples of problem solution

Example 4. The endless direct wire is located perpendicularly to the plane of the current coil and is situated at a distance of a=5сm from its centre. A current in the wire I₁=10A, a current in the coil I₂=3A. Current’s direction is shown in the picture. Radius of coil R=3сm. Find the magnetic field induction in the centre of coil.

Input: I1=10A; I2=3A; a=5сm=5×10-2 m; R=3сm=3×10-2 m.	a)Parallelogram rule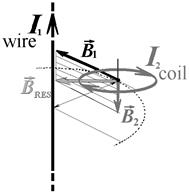
Find: В – ?

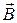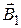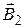Solution: In accordance with the superposition principle of magnetic fields the magnetic induction equals the vector sum of the magnetic field inductions and at the centre of coil, which are created in this point with the individual currents I₁ and I₂:

.

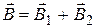1) We must show the directionof the resultant vector of magnetic induction defined by parallelogram rule to the diagrammatic drawing (see picture a)).

Let’s find direction of a vector 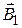with the right-hand rule (see picture b)). The thumb direction should coincide with a direction of a current I₁. The curled fingers points in the direction of the field line. Vector of magnetic field lies along a tangent to the field line. The straight forefinger of right hand points in the direction of vector of magnetic field .

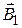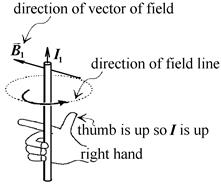b)Right-hand rule	c)Screw rule

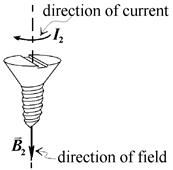
Let’s find direction of a vector 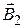with the screw rule (see picture c)). Rotational motion of screw should coincide with a direction of a current I₂. Translational movement of screw points in the direction of vector of magnetic field .

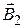The resultant vector 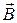is defined with parallelogram rule of the vectors’ additions (see picture b)).

2) We define the magnitude of the resultant vector with cosine theorem:

.

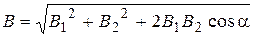As the vector 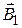is perpendicular to a current I₁, and the vector 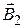lies in the plane of a current I₁, then angle is between the vectors a=90^o (cos90^o=0). Therefore cosine theorem will be conversed to a Pythagorean theorem:

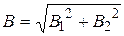. (1)

We find the magnetic field induction of the infinitely long straight wire with a current in the air with the formula

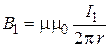, (2)

where m₀=4p×10^–7 H/m – permeability of vacuum; r=a – distance from the wire to the target point.

The magnetic field induction in the centre of the coil with radius of R

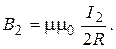(3)

Substituting (2) and (3) in the formula (1) in the given case m=1, we’ll get:

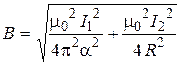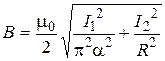, or . (4)

Check if the right part of the formula gives us (4) the unit of magnetic induction [Т]

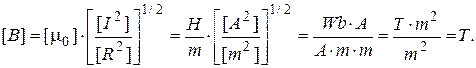
Let’ make the calculations:

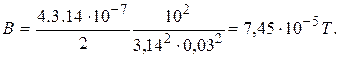
Result: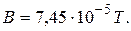

Example 5. Over the infinitely long wire, so bent, as it’s shown in the picture, current flow 5А. Radius of the arc 5cm. Find the intensity of the magnetic field in the point О.

Input: I=5 А R=5cm=5×10-2 m;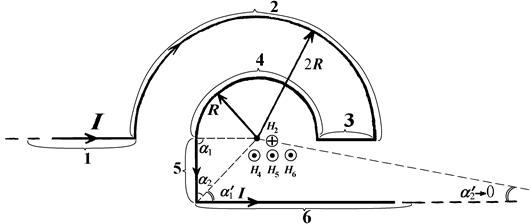
Find: Н – ?

Solution:

We’ll find 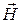the magnetic field intensity in the point О using the superposition principle of fields. In the given case wire can be divided into six segments: four straight segments: №1, №3, №5 and №6 and two arcs of the semicircles: №2 and №4 (see picture). The magnetic field intensity in the target point is equal to the vector sum of the intensities, which are created with six segments:

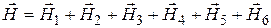. (1)

The magnitude of magnetic intensity vector, which is created with the element of a current I 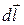, is found from Biot-Savart-Laplace law:

,

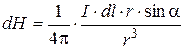where a – angle between the radius-vector to the target point and the element of a current I .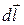

As the point О lies on the axis of the segment №1 and №3, the radius-vectors lies on the direction of corresponding currents. Then a₁=a₂=0 and H₁=H₃ = 0

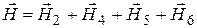. (2)

The vectors’ directions of intensity of straight segments №5 and №6 are found with the right-hand rule, and the vectors’ directions of intensity of semicircles: №2 and №4 are found with the screw rule.

We find the vectors’ directions of intensity with the right-hand screw rule. Vector 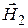is perpendicularly directed to the plane of the picture from an observer, vectors 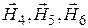– to the observer. Taking into account the direction to an observer, we replace the vector equality (1) with scalar.

H=H₄+ H₅+ H₆ – H₂ .

We find magnitudes of arcs’ vectors of the semicircles №2 and №4 using the formula of calculation for the filed intensity in the centre of coil

.

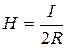Radiuses of semicircles R₂=2R and R₄=R (see picture). In the given case the magnetic field is created only with the half of such loop current, that’s why

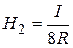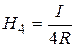and . (3)

We find magnitudes of vectors of straight segments №5 and №6 using the formula of calculation for the filed intensity of segment of straight wire

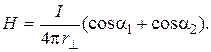
where r_^ – the smallest distance from the wire to the point, where the intensity is situated; a₁ and a₂ – angels, which are created radius-vectors, traced from the ends of a conductor to the target point.

For the segment №5: r_^ =R; a₁=90⁰; cosa₁=0; a₂=45^o; cos a₂= √2/2, then

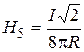. (4)

For the segment №6: r_^ =R; a₁=45^o; cosa₁=√2/2; a₂®0; cos a₂®1 , then

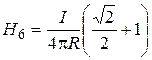. (5)

Inserted (3), (4) and (5) in the formula (2), we’ll get

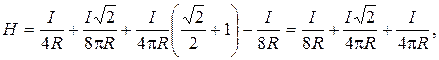
or 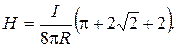. (5)

Check if the right part of the formula gives (5) the unit of the magnetic field intensity [А/m]

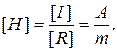
Let’s make the calculations:

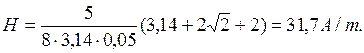
Result: H=31,7 A/m.