Вивчення ВИмушених коливань лінійного та нелінійного осцилятора
3.1 Мета роботи
Вивчити закономірності процесів установлення коливань осцилятора під дією зовнішньої гармонічної сили, коли квазіпружня (повертаюча) сила має лінійну та нелінійну залежності від зміщення.
3.2 Вказівки з організації самостійної роботи
Вимушені коливання, що відбуваються під дією нелінійної повертаючої сили описуються диференціальним рівнянням [1, 4]
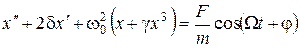 , (3.1)
, (3.1)
де 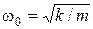 – власна частота осцилятора;
– власна частота осцилятора;
δ – коефіцієнт згасання, 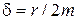 ;
;
r – коефіцієнт опору;
m – маса осцилятора;
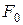 – амплітуда сили, що змушує;
– амплітуда сили, що змушує;
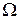 – частота сили, що змушує;
– частота сили, що змушує;
γ – стала величина, яка характеризує нелінійність повертаючої сили.
Коли сила, що змушує, діє за лінійним законом ( 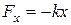 ,
, 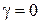 ) в системі встановлюються гармонічні коливання з частотою
) в системі встановлюються гармонічні коливання з частотою 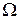 цієї сили
цієї сили
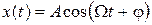 , (3.2)
, (3.2)
де амплітуда А та початкова фаза 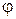 визначаються за формулами:
визначаються за формулами:
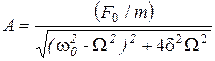 та
та 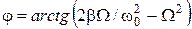 . (3.3)
. (3.3)
При певній для даної системи частоті (резонансній частоті)
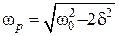 (3.4)
(3.4)
амплітуда коливань досягає максимального значення
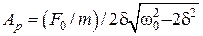 . (3.5)
. (3.5)
Коли повертаюча сила є нелінійною функцією зміщення, вона може бути наведена у вигляді ряду
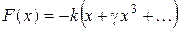 . (3.6)
. (3.6)
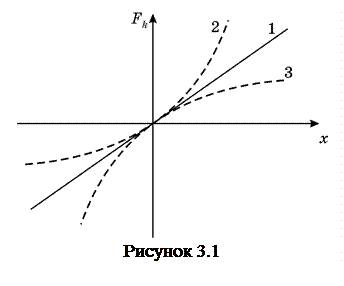
Коли γ > 0, квазіпружна сила більша ніж, у лінійному випадку. Якщо це сила пружності пружини, то таку пружину називають “жорсткою”. Коли γ < 0, сила менша, ніж у лінійному випадку, і пружину називають “м’якою”. На рис.3.1 наведені криві залежності квазіпружної сили від зміщення х відповідно: (1) – для лінійної залежності, (2) – для “жорсткої” пружини. (3) – для “м’якої” пружини.
 В системі з нелінійною повертаючою силою такий резонанс, як у лінійному випадку, неможливий. Якщо γ > 0, власна частота збільшується зі зростанням амплітуди. Отже, на кривій залежності амплітуди від частоти максимум буде нахилений вправо (рис.3.2,а). Якщо γ < 0, максимум буде нахилений вліво (рис.3.2,б). Отже, одному значенню частоти відповідає декілька значень амплітуди і можливі ударні скачки амплітуди. Якщо графік залежності
В системі з нелінійною повертаючою силою такий резонанс, як у лінійному випадку, неможливий. Якщо γ > 0, власна частота збільшується зі зростанням амплітуди. Отже, на кривій залежності амплітуди від частоти максимум буде нахилений вправо (рис.3.2,а). Якщо γ < 0, максимум буде нахилений вліво (рис.3.2,б). Отже, одному значенню частоти відповідає декілька значень амплітуди і можливі ударні скачки амплітуди. Якщо графік залежності 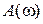 будується, починаючи зі значень
будується, починаючи зі значень 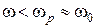 – крива йде шляхом c–d–e–f, якщо починати зі значень
– крива йде шляхом c–d–e–f, якщо починати зі значень 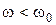 – крива йде шляхом f–e–k–c.
– крива йде шляхом f–e–k–c.
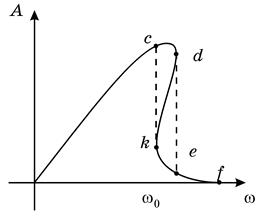
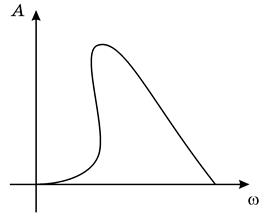
а) б)
Рисунок 3.2
3.3 Опис комп’ютерної програми
Для вивчення вимушених лінійних і нелінійних коливань використо-
вується та сама програма, що й для вивчення вільних коливань (робота 2), але крім режиму 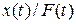 в даній роботі використовується режим
в даній роботі використовується режим 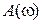 , який дозволяє отримувати залежність амплітуди коливань від частоти як у випадку лінійних (γ= 0), так і нелінійних коливань (γ> 0). Зовнішній вигляд інтерфейсу програми у цьому режимі зображено на рисунку 3.3. На екран
, який дозволяє отримувати залежність амплітуди коливань від частоти як у випадку лінійних (γ= 0), так і нелінійних коливань (γ> 0). Зовнішній вигляд інтерфейсу програми у цьому режимі зображено на рисунку 3.3. На екран
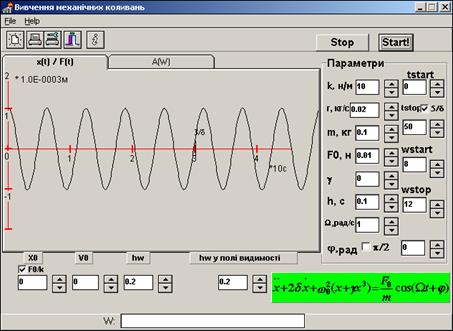
Рисунок 3.3
виведені кнопки: k – жорсткість пружини; r – величина опору; m – маса частини, що коливається; F0 – амплітуда сили; γ – коефіцієнт нелінійності; h – крок для побудови плавної кривої 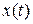 ; w – крок, який впливає на плавність кривої
; w – крок, який впливає на плавність кривої 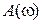 ;
; 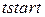 ,
, 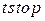 – кнопки, що регулюють початок та кінець побудови графіка х(t);
– кнопки, що регулюють початок та кінець побудови графіка х(t); 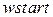 ,
, 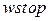 – кнопки, що визначають межі побудови графіка
– кнопки, що визначають межі побудови графіка 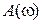 ;
; 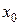 – початкове зміщення;
– початкове зміщення; 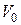 – початкова швидкість.
– початкова швидкість.
3.4 Інструкція користувачу
1. Задати значення m і k згідно з табл. 3.1 та натиснути кнопку «Start». Визначити власну частоту осцилятора 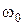 .
.
2. Вибрати режим роботи: 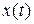 . Встановити крок h=0,005. Задати значення величин згідно з табл. 3.1.
. Встановити крок h=0,005. Задати значення величин згідно з табл. 3.1.
3. Отримати графіки 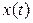 коливань при γ = 0 за початкових умов
коливань при γ = 0 за початкових умов 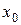 – згідно з табл. 3.1,
– згідно з табл. 3.1, 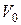 =0 у трьох випадках :1)
=0 у трьох випадках :1) 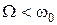 , 2)
, 2) 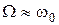 , 3)
, 3) 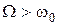 . Зарисувати отримані графіки. Вказівки :
. Зарисувати отримані графіки. Вказівки :
1) якщо криві виходять ламаними, зменшити крок 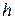 (
( 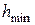 =0,001);
=0,001);
2) якщо встановлення амплітуди коливань відбувається за екраном, збільшити час переглядання.
4. Повторити операції п.3 за початкових умов 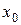 =0,
=0, 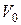 згідно з табл. 3.1.
згідно з табл. 3.1.
5. Встановити режим програми 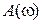 . Отримати графіки залежності
. Отримати графіки залежності 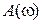 при трьох значеннях коефіцієнта опору
при трьох значеннях коефіцієнта опору 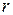 =0,01; 0,05; 0,1 (покласти
=0,01; 0,05; 0,1 (покласти 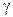 =0). Перерисувати на один графік три резонансній криві. Зробити висновок про вплив величини згасання на ширину резонансної кривої та максимальне значення амплітуди коливань (параметри k і m встановити згідно з табл. 3.1).
=0). Перерисувати на один графік три резонансній криві. Зробити висновок про вплив величини згасання на ширину резонансної кривої та максимальне значення амплітуди коливань (параметри k і m встановити згідно з табл. 3.1).
Таблиця 3.1 – Вихідні дані
| Номер вар. | k , 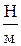 | m, кг | 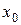 , м , м | 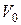 , , 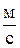 | Номер вар. | k , 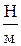 | m, кг | 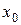 , м , м | 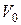 , , 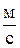 |
| 0,1 | 0,02 | 0,2 | 0,1 | 0,04 | 0,2 | ||||
| 0,1 | 0,02 | 0,4 | 0,1 | 0,04 | 0,4 | ||||
| 0,1 | 0,02 | 0,6 | 0,1 | 0,04 | 0,6 | ||||
| 0,1 | 0,02 | 0,8 | 0,1 | 0,04 | 0,8 | ||||
| 0,1 | 0,02 | 1,0 | 0,1 | 0,04 | 1,0 | ||||
| 0,1 | 0,02 | 1,2 | 0,1 | 0,04 | 1,2 |
6. Надаючи позитивні значення γ (випадок “жорсткої пружини”), отримати резонансну залежність 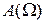 . Зарисувати (якісно) отриману криву.
. Зарисувати (якісно) отриману криву.
7. Надаючи негативні значення γ (випадок “м’якої пружини”) спостерігати на екрані резонансну криву. Зарисувати отриману криву.
8. Зробити висновок відносно впливу нелінійності на форму резонансної залежності та величину резонансної частоти 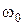 в порівнянні з лінійним випадком (γ = 0).
в порівнянні з лінійним випадком (γ = 0).
3.5 Зміст звіту
Звіт має містити: мету роботи, результати вимірювань, графіки та висновки за пунктами 3...7.
3.6 Контрольні запитання і завдання
1. Які коливання називаються вимушеними?
2. Запишіть рівняння, яке описує вимушені коливання. Який вигляд має його розв’язок?
3. В чому полягає явище резонансу? За яких умов воно може виникнути? Проаналізуйте вираз для амплітуди коливань і зсуву фаз між швидкістю та силою.
4. Коли виникають нелінійні коливання?
5. Чим відрізняються резонансні криві при нелінійних коливаннях?
