Подставив в (2) все известные величины, мы получим значение

R⁰ = 8314 Дж/(кмоль К).

Другой известный закон Авогадро гласит, что в одном киломоле любого вещества содержится одинаковое количество структурных единиц (молекул, атомов). Это число называется числом Авогадро: N_A = 6,02 10²⁶ кмоль^-1.

Тогда в уравнении (2) количество киломолей n_m можно выразить через общее количество молекул N : n_m = N/ N_A. При подстановке в (2) получим:

PV = (N/ N_A )R⁰T. Величина R⁰/ N_A =k = 1,38 10^-23 Дж/К – новая константа, называемая постоянной Больцмана. С учетом того, что величина N/V = n – концентрация частиц в объеме V, уравнение состояния можно записать в виде

P = n k T. (3)

Таким образом, постоянная Больцмана устанавливает связь между термодинамическим и молекулярно-кинетическим подходами к изучению состояний систем.

Лекция №2

Смеси идеальных газов. Первое начало термодинамики.

1. Смеси идеальных газов.

Пусть газ представляет собой не реагирующую смесь из нескольких компонент. Как будет выглядеть уравнение состояния такого газа? Существуют два подхода к рассмотрению таких систем: массовый и объемный состав смеси.

Рассмотрим массовый состав смеси: m_см = ∑m_i и введем массовую долю газовой компоненты g_i = m_i/m_см; ∑ g_i = 1. Введем также понятие парциального давления Р_i : это давление, которое оказывала бы i-тая компонента газа, если бы она одна занимала весь объем смеси при температуре смеси. Для давления смеси существует закон Дальтона: Р_см = ∑ Р_i. Это утверждение легко проверить, если воспользоваться уравнением состояния для смеси в виде (3), представив количество молекул в смеси в виде суммы молекул отдельных компонент и соответственно концентрацию смеси в виде суммы их концентраций. Чему же равна газовая постоянная смеси R_см? Для вывода R_см запишем уравнения:

P_смV_см = m_смR_смT_см, (4)

Р_i V_см = m_i R_i T_см (5)

Просуммируем уравнения (5) по всем i и сравним с (4). Левые части этих уравнений оказались равными, тогда из равенства правых частей получим:

m_смR_см = ∑ m_i R_i , (6)

откуда R_см = ∑ m_i / m_см R_i =∑ g_i R_i = R⁰ ∑ g_i /m_i . (7)

Рассмотрим объемный состав смеси. Парциальный объем V_i – это объем, который имела бы i-тая компонента смеси при Р = Р_см и Т = Т_см. Таким образом, можем записать

Р_смV_i = m_iR_iT_см (8)

Сравнив это выражение с (5), получим Р_смV_i = Р_i V_см, откуда следует:

P_i = P_cмr_i , где r_i = V_i/V_см – объемная доля смеси.

Найдем молекулярную массу смеси. Для этого уравнения (4) и (8) перепишем в виде:

P_смV_см = m_см /μ_см R⁰T_см, (9)

Р_смV_i = m_i /μ_iR⁰T_см (10)

(10) разделим на (9) и проведем суммирование по всем индексам. Легко видеть, что μ_см = ∑ μ_i r_i (11).

Теперь осталось установить связь между массовой и объемной долями компонентов смеси.

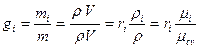(12)

Полученных формул достаточно для рассмотрения свойств газовых смесей.

2. Первое начало термодинамики.

Первое начало, или первый закон, термодинамики представляет собой закон сохранения энергии в применении к тепловым процессам. Необходимо ввести понятие внутренней энергии термодинамической системы. Внутренняя энергия U термодинамической системы есть суммарная полная энергия составляющих ее частиц. Для газа это сумма кинетических энергий всех молекул плюс энергия взаимодействия молекул между собой (движения системы как целого мы не рассматриваем и потенциальную энергию системы в поле тяжести Земли считаем равной нулю). Если не делать предположения об идеальности газа, то внутренняя энергия есть функция двух параметров состояния: температуры Т (т.к. средняя кинетическая энергия молекул зависит от температуры газа) и объема V, так как энергия взаимодействия молекул зависит от их взаимных расстояний. Поскольку для идеального газа энергией взаимодействия молекул мы пренебрегаем, то для него U = U(T) – является функцией только температуры.

Если хотя бы один из параметров состояния системы изменяется, то в системе совершается термодинамический процесс, в результате которого она переходит в новое состояние. Какие воздействия на систему могут вызвать такой переход? Существует два способа передачи энергии системе, в результате чего она переходит в новое состояние: сообщение системе некоторого количества теплоты и совершение над системой работы.

Сообщение системе тепла связано с понятием теплоемкость. Теплоемкостью С[Дж/К] называют величину, равную количеству теплоты, которое надо сообщить телу, чтобы повысить его температуру на один градус. Если рассчитать это количество теплоты на единицу массы тела, то получим удельную теплоемкость с [Дж/кгК]. Тогда количество тепла, сообщенное системе, можно вычислить по формуле: dQ = mcDT (в том случае, если с = const). Для газов оказывается, что для повышения температуры на одну и ту же величину DT требуется сообщить различное количество теплоты в зависимости от процесса, в котором эта теплота сообщается. Поэтому существует два вида теплоемкости: теплоемкость при постоянном объеме c_v и теплоемкость при постоянном давлении с_р. Различие между ними станет ясным из дальнейшего изложения.

Работу, совершаемую газом при расширении (или производимую над ним при сжатии), легко рассчитать, рассматривая расширение газа в цилиндре с поперечным сечением S под поршнем: dА =Fdx =PSdx =PdV. Равновесное состояние газа часто изображают графически на диаграмме PV в виде точки на плоскости, а процесс перехода из одного состояния в другое – в виде кривой, или графика, процесса. Тогда работу, произведенную в процессе, графически можно изобразить в виде площади под этой кривой: .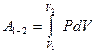

P

V

Давление Р в этой формуле нужно рассматривать как функцию объема V.

Теперь можем сформулировать первое начало термодинамики как закон сохранения энергии в тепловых процессах: тепловая энергия, подведенная к термодинамической системе, расходуется на изменение ее внутренней энергии и на работу, производимую системой против внешних сил.

В термодинамике часто рассматриваются термодинамические циклы, т.е. процессы, в результате которых система возвращается в исходное состояние.

Первое начало утверждает, что если система совершает термодинамический цикл, то полное количество теплоты, сообщенное системе, равно совершенной ею работе. Математическая формулировка первого начала:

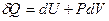(13)

Все величины в формуле (13) могут быть рассчитаны на единицу массы системы. Тогда вместо (13) имеем:

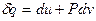, (14)

где v – удельный объем.

Для идеального газа внутренняя энергия системы является функцией только состояния газа, ее изменение в термодинамическом процессе не зависит от типа процесса, а зависит только от состояния, в которое перешла система. Поэтому dU (du) является полным дифференциалом. В отличие от внутренней энергии работа (это хорошо видно на диаграмме), как и теплота являются функциями процесса. Поэтому выражения dQ, dA полными дифференциалами не являются.

Полный дифференциал внутренней энергии газа в общем случае может быть записан как

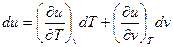(15)

Чему равна величина первого члена в правой части формулы? Допустим, что мы применили первое начало (14) к изохорному процессу (V=const.). Из (14) следует, что 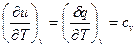, и удельная теплоемкость при постоянном объеме характеризует темп роста внутренней энергии с температурой. Для идеального газа (пренебрегаем взаимодействием молекул) второй член в (15) отсутствует, т.е. 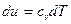. Таким образом, уравнение первого начала для идеального газа записывается в виде:

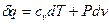(16)

Внутренняя энергия является термодинамической функцией состояния системы. Существуют и другие функции состояния; одной из них является

энтальпия (ее называют также теплосодержанием). Вернемся к формуле (14) для первого начала термодинамики. Заметим, что Pdv =d(Pv) – vdP, и подставим это выражение в формулу:

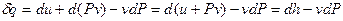, (17)

где функция h = u +Pv – удельная энтальпия системы. Как и внутренняя энергия, энтальпия для идеального газа является функцией только температуры системы. Уравнение (17) есть вторая форма записи первого закона термодинамики – через энтальпию. В общем случае принято считать, что энтальпия является функцией температуры и давления системы. Тогда полный дифференциал энтальпии в общем случае можно записать как:

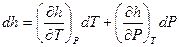(18)

Что такое 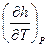? Применим уравнение (17) к изобарному (Р = const) процессу. Тогда получим, что 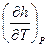= 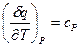; для идеального газа второй член в правой части формулы (18) отсутствует, и удельная теплоемкость с_Р характеризует темп роста энтальпии с температурой. Для идеального газа уравнение (17) может быть переписано в виде:

.

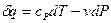(19)