Мера информации по Шеннону

Сообщения могут быть закодированы разными символами. Число разных символов, из которых образуются сообщения, составляет основание кода, (русский алфавит имеет 33 символа, двоичный код – 2 символа, код Бодо – 5 символов и т.д.).

Совокупность различных символов, составляющих основание кода, назовем алфавитом.

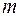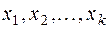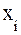Пусть - основание кода и передается последовательность , где - один из символов из алфавита. Число всевозможных сообщений, которые можно создать равно 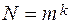. Информация, содержащаяся в ансамбле из N сообщений, должна быть пропорциональна длине последовательности. Р. Хартли в 1928 г. предложил за меру количества информации в ансамбле из N сообщений принять величину

.

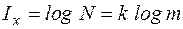Но мера информации по Хартли не учитывает вероятностный характер появления элементов последовательности .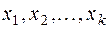

Мера – это одна из характеристик исследуемого объекта. Это может быть длина, ёмкость и т.д. В данном случае необходимо определить меру информации, содержащемся в каждом элементе ансамбля и среднюю меру информации в ансамбле в целом.

Мера должна обладать двумя свойствами:

1. мера исследуемого объекта не должна быть отрицательной,

2. если объект состоит из нескольких элементов, каждый обладающий определённой мерой, полная мера объекта равна суме мер отдельных составляющих, (условие аддитивности) .

Пусть ансамбль 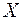состоит из элементов 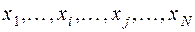. Выберем два элемента 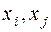из этого ансамбля, имеющих совместную вероятность реализации этих элементов

.

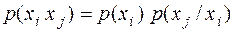Обозначим через 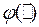меру информации, содержащемся в элементе . Тогда, используя свойство аддитивности меры, запишем меру информации, содержащуюся в ансамбле из двух элементов , ,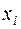

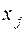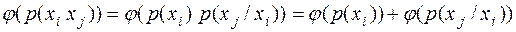. (2.1)

Дифференцируя левую и правую части выражения (**.1) по 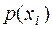, получим

.

.

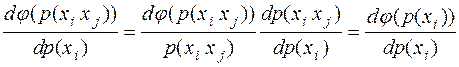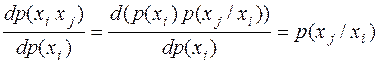В результате имеем

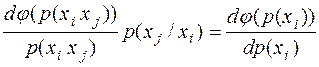
Умножив обе части полученного равенства на 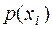, получим уравнение

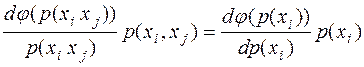. (2.2)

Уравнение (***.2) имеет решение, если

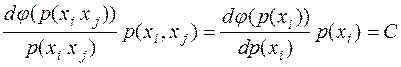, (2.3)

где С – постоянная величина.

Интегрируя уравнение (***.3), получим

,

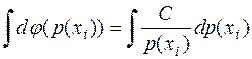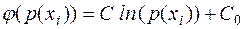(2.4)

Определим 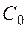из условия: если событие 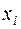происходит с вероятностью 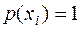, то оно не несёт никакой информации для абонента. Поэтому функция 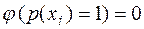и .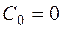

Так как мера информации не должна быть отрицательной, а 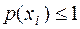, то коэффициент 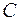должен быть отрицательным. Если 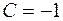, то мера информации имеет вид

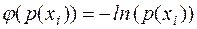
и измеряется в неперах, [Неп]. Однако на практике, ввиду развития цифровой техники и использования двоичной системы счисления чаще применяется основание логарифма, равное 2. Тогда 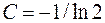и мера информации, или количество информации, содержащаяся в элементе 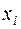, будет равна

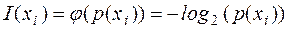. (2.5)

В дальнейшем основание логарифма 2 будем опускать. Мера информации 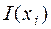измеряется в битах, (Бит).

Каждый элемент ансамбля обладает своим количеством информации 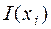, реализующимся с вероятностью 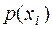. Таким образом, мера информации – это характеристика элемента ансамбля 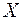, являющаяся случайной величиной с реализациями в виде количества информации 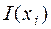, появляющихся с вероятностями 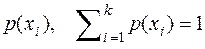, (Таблица 1).

Таблица 2.1
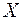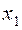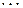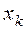P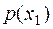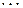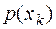
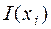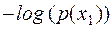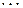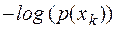