Вивчення магнітного поля кругового

Витка та соленоїда

11.1 Мета роботи

Ознайомитись із законом Біо-Савара-Лапласа, дослідити магнітне поле контуру зі струмом та системи співвісних контурів, які утворюють котушку з струмом, базуючись на законі Біо-Савара-Лапласа.

11.2 Вказівки з організації самостійної роботи.

Магнітне поле 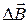елемента струму ( 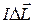) визначається за законом Біо-Савара-Лапласа [2, 5]:

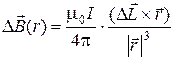, (11.1)

де 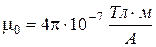– магнітна стала, І – величина постійного електричного струму, 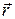– радіус-вектор, який характеризує положення точки, в якій створюється величина індукції 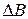по відношенню до елемента .

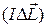Закон Біо-Савара-Лапласа має загальний характер і в принципі може бути використаний для визначення магнітного поля, яке створюється провідником із струмом будь-якої форми. Зрозуміло, що ніяких ізольованих ділянок струму не буває і провідник має утворювати замкнене коло. Однак ми можемо наближено уявити безперервний провідник у вигляді ряду дискретних ділянок. Тоді вектор індукції 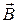в будь-якій точці простору можна визначити за допомогою принципу суперпозиції. Для нашого випадку кінцевих елементів струму

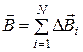, (11.2)

де m − кількість елементів, на які розбивається контур. В скалярному вигляді

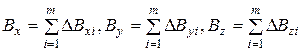. (11.3)

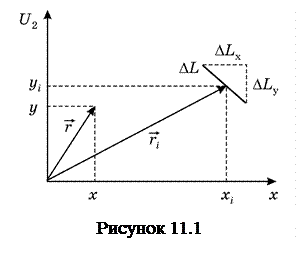
Вклад кожної з ділянок довжиною 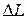, розташованої в точці 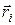, в магнітне поле в точці 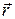(рис.11.1) визначається за формулами (в проекціях)

,

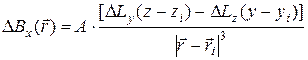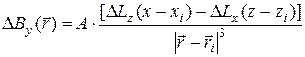, (11.4)

,

де

.

Для магнітного поля на вісі, що проходить через центр системи витків можна отримати аналітичний вираз

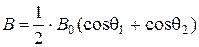, (11.5)

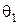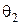де кути та показані на рис.11.2, на якому схематично зображена котушка зі струмом, В₀ − індукція всередині довгого соленоїда

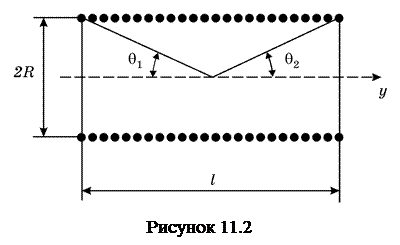
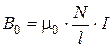. (11.6)

11.3 Опис комп’ютерної програми

Зовнішній вигляд інтерфейсу програми зображено на рис. 11.3. Програма обчислює та рисує силові лінії магнітного поля кругового витка зі струмом, який знаходиться в площині xz, та системи N співвісних витків (див. рис.11.2).

Оскільки система має вісь симетрії, досить подати силові лінії в одній площині, яка проходить крізь неї. Цією площиною є площина xy, вона висту­пає в ролі екрана. Обчислення виконуються за формулами (11.3), (11.4). Інтерфейс програми має основну та дві допоміжні панелі. На основній панелі виводяться вікна з параметрами котушки: це радіус витка, висота соленоїда, кількість елементів, на які розбивається виток при обчисленні індукції та загальна кількість елементів котушки. На одній з допоміжних панелей можна вибрати координати точки, з якої програма починає викреслювати силові лінії. За допомогою другої панелі можна визначити під яким кутом рисувати силові лінії в тривимірному просторі. Програма обчислює значення індукції в будь-якій точці. Підводячи курсор в будь-яку точку можна “виміряти” індукцію В та координати точки. Програма дозволяє також регулювати швидкість викреслювання силових ліній та їх густину. Розміри на екрані дисплея вимірюються в пікселях.

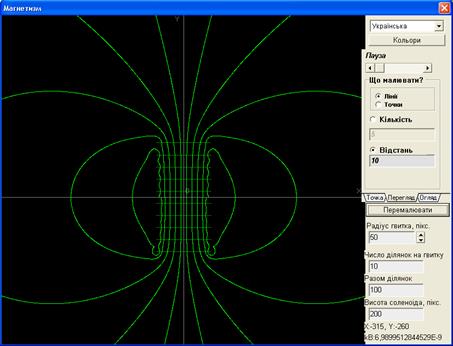
Рисунок 11.3

11.4. Інструкція користувачу

1. Створити один виток із струмом. Для цього вибрати однакову кількість “ділянок на витку” та “разом ділянок”. “Відстань” між лініями, яка регулює густину ліній дорівнює 20 пікселям. Отримати картину силових ліній для магнітного поля одного витка. Зарисувати її. Зазначити на рисунку координати центра витка та значення індукції.

Збільшуючи кількість “ділянок на витку” в два, три і т.д. разів, прослідкуйте, як змінюється точність розрахунку (шляхом порівняння 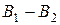, , і т.д. різниця 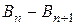має зменшуватись). Вибираючи “кут нахилу” прослідкуйте, як змінюється при цьому апроксимація кругового витка ломаною лінію, внаслідок його розбивки на елементи .

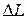3. Встановити довжину котушки L=200 пікселів, R=50 пікселів, координати початкової точки для розрахунку силової лінії покладіть рівними 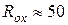пікселів, 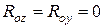. Збільшити густину силових ліній (шляхом зменшення “відстані”), встановити “Разом ділянок” − 30. Збільшити кількість витків. Прослідкуйте, як поводять себе силові лінії (яка їх форма) поблизу витків, чи перетинають вони циліндричну поверхню, на якій знаходяться витки?

4. Визначити значення індукції в центрі соленоїда (параметри взяти з табл. 11.1). Зняти залежність В(L), тобто визначити шість разів В в центрі соленоїда для шести різних значень довжини котушки L. Результати занести в таблицю.

5. Встановити параметри соленоїда у відповідності з табл. 11.1. Виміряти та записати 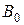в центрі соленоїда. Визначити ще шість значень В для шести значень відстані y від центра соленоїда. Результати занести в таблицю.

Таблиця 11.1 – Вихідні дані

Номер вар.	L, пікс	R, пікс	Разом ділянок	Номер вар.	L, пікс	R, пікс	Разом ділянок

6. Побудувати за пунктом 4 графік 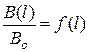, зробити висновок, як змінюється відношення 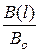зі зростанням довжини соленоїда.

7. Побудувати за пунктом 5 графік 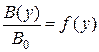. На одному рисунку для порівняння побудуйте залежність . Зробити висновок.

11.5 Зміст звіту

Звіт має містити: мету роботи, картину силових ліній для магнітного поля одного витка, результати вимірювань, зведені в таблиці, графіки 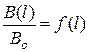та .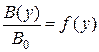

11.6 Контрольні запитання і завдання

1. Що таке “елемент струму”?

2. Запишіть закон Біо-Савара-Лапласа у векторній та скалярній формах.

3. В чому принцип суперпозиції для магнітного поля?

4. Запишіть формулу для індукції довгого соленоїда.

5. За яких умов соленоїд можна вважати нескінченно довгим?

6. Вивести формулу для індукції магнітного поля у центрі нескінченно довгого соленоїда.