Броунівський рух. Досліди Перена по визначенню числа Авагадро

Суть броунівського руху

Англійський ботанік Броун у 1827 році виявив, що дрібні частинки 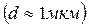, наприклад, спори папороті, які зважені у воді, здійснюють неперервні хаотичні рухи. Такий хаотичний рух дрібних частинок, зважених у рідині або газі, отримав назву броунівського.

Особливості:

1. Швидкість руху броунівських частинок збільшується зі зростанням температури та зі зменшенням розмірів частинок ( ).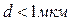

2. Характер броунівського руху не залежить від властивостей речовини частинок, а залежить лише від властивостей рідини чи газу, в яких ці частинки зважені.

Вказані закономірності можна пояснити, припустивши, що броунівський рух виникає внаслідок ударів з боку молекул рідини або газу.

Оскільки рух молекул хаотичний можна очікувати, що число ударів з боку молекул о частинку в будь-якому напрямку дорівнюватиме числу ударів у протилежному напрямку. В результаті частинка залишиться нерухомою. Але це твердження буде справедливе лише для великих проміжків часу, і тільки в середньому число ударів у різних напрямках буде однаковим. Якщо ж мова йде про малі проміжки часу і малі об’єми рідини чи газу, а також у випадках, коли число ударів N – невелике, то можливі відхилення від середніх значень.

Такі відхилення від середнього значення будь якої величини, які виникають в малому об’ємі але за мали проміжки часу називаються флуктуаціями. І оскільки ми розглядаємо малі частинки, то для них перевага ударів з якого-небудь боку буде помітною.

Таким чином, броунівський рух можна пояснити так. Внаслідок флуктуації числа ударів молекул о частинку, виникає деяка результуюча сила певного напрямку. Оскільки флуктуація звичайно є недовгочасною, то через деякий проміжок часу напрямок результуючої сили змінюється, а разом з ним змінюється і напрям переміщення частинки.

Хаотичність руху зважених частинок є віддзеркаленням хаотичності молекулярного руху.

Рівняння Ейнштейна-Смолуховського для броунівського руху

Як ми з’ясували раніше, внаслідок неповної компенсації ударів молекул з протилежних боків, на броунівську частинку діє на протязі короткого часу деяка сила F. Окрім неї, на частинку, яка рухається за рахунок сили F, діє ще сила тертя ¦, що напрямлена проти F.

Пам’ятаємо, що сила тертя (сила Стокса):

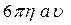¦ = (1)

де а– радіус частинки, u– швидкість її руху, h– коефіцієнт внутрішнього тертя (в’язкості).

Тоді рівняння руху частинки в проекціях на вісь Ох буде мати вигляд:

¦

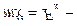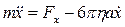(2)

Наша задача полягає в тому, щоб знайти середнє значення зміщення Dx частинки, яке відбувається за час Dt внаслідок ударів молекул. Точніше, потрібно знайти середнє значення 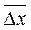багатьох послідовних переміщень 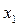D , D 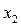,..., D 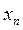, які відбулися за рівні проміжки часу
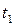D = D 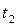= ... = D 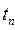. Оскільки окремі переміщення D 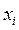відрізняються як за величиною, так і за напрямком, то їх сума, а отже і 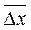, можуть виявитися рівними нулю. Тому видозмінимо задачу і будемо шукати середнє значення квадрату зміщення, тобто величину .

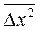Перетворимо (2) таким чином, щоб ця формула включала в себе 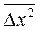. Помножимо обидві частини рівняння на x:

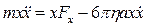(3)

При цьому:

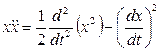
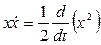
Підставимо отримані рівності у (3):

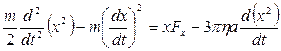(4)

Оскільки ця рівність справедлива для довільного зміщення 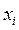, то вона буде виконуватися і для середніх значень величин, які входять до неї, 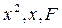, якщо зміщень 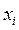було досить багато:

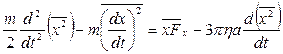(5),

де 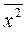– середнє значення квадрату зміщення частинки, 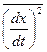– середнє значення квадрату її швидкості, 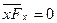, оскільки x і 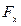можуть однаково часто приймати додатні і від’ємні значення.

Таким чином, рівняння (5) приймає вигляд:

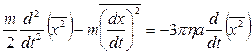(6)

Зауважимо, що 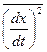– середнє значення проекцій швидкості на вісь x. В силу хаотичності руху частинки:

= =

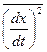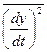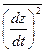
Вочевидь також:

= = =

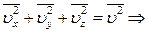
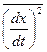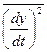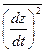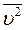
Отже:

=

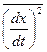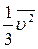
Тому

= = = =

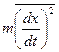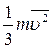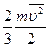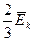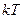
де 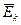= = 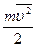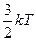– середня кінетична енергія броунівського руху частинок.

Зіштовхуючись з молекулами, броунівська частинка обмінюється з ними енергією і знаходиться у стані теплової рівноваги з середовищем (рідиною), у якому рухається. Тому 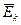броунівської частинки повинна дорівнювати 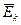молекул рідини або газу, остання ж дорівнює 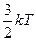. Ось чому:

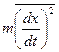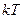= (7)

Рівняння (6) з урахуванням (7) перепишеться у вигляді:

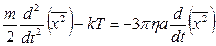(8)

Позначимо =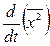

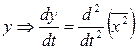
Одержимо новий вираз:

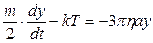(9)

Розділимо у цьому рівнянні змінні:

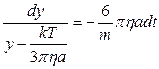
Отриманий вираз проінтегруємо: ліву частину – у межах від 0 до y, а праву – від 0 до t. В результаті:

=

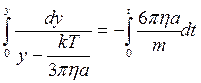
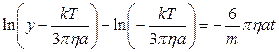
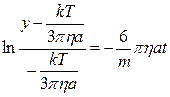
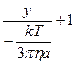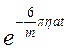
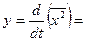
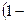
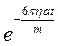
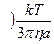(10)

Проаналізуємо отриману рівність. У звичайних умовах а~ 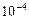см, h ~ 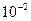, таким чином дріб 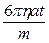приймає досить великі значення при 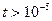с. А це означає, що величиною 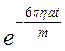можна знехтувати. В результаті:

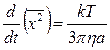(11)

Для кінцевих проміжків часу Dt і відповідних переміщень 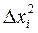рівняння Ейнштейна-Смолуховського можна записати у вигляді:

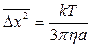Dt (12)

Середнє значення 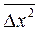квадратів багатьох переміщень 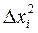броунівської частинки за проміжок часу Dt вздовж вісі x (або будь-якої іншої) пропорційне цьому проміжку часу.

Дослід Перрена [2, ст.47-48 або 7, ст. 213-214]