Дифракция света. Принцип Гюйгенса-Френеля. Метод зон Френеля. Дифракция Френеля на простейших преградах.

Дифракция – совокупность явлений, наблюдаемых при распространении световых волн в среде с препятствиями и связанных с отклонениями от законов геометрической оптики.

Между дифракцией и интерференцией нет принципиального различия.

Различают два вида дифракции:

1)Дифракция Френеля – дифракция в сходящихся лучах, осуществляемая в том случае, когда дифракционная картина наблюдается на конечном расстоянии от препятствия, вызвавшего дифракцию.

2)Дифракция Фраунгофера наблюдается в том случае, когда источник света и точка наблюдения бесконечно удалены от препятствия, вызвавшего дифракцию. Чтобы этот тип дифракции осуществить, достаточно точечный источник света поместить в фокусе собирающей линзы, а дифракционную картину исследовать в фокальной плоскости второй собирающей линзы, установленной за препятствием.

Принцип Гюйгенса-Френеля.

Явление дифракции объясняется с помощью принципа Гюйгенса,согласно которому каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн задает положение волнового фронта в следующий момент времени.

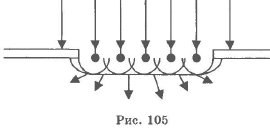
Пусть плоская волна нормально падает на отверстие в непрозрачном экране. Согласно Гюйгенсу, каждая точка выделяемого отверстием участка волнового фронта служит источником вторичных волн (в однородной изотропной среде они сферические). Построив огибающую вторичных волн для некоторого момента времени, видим, что фронт волны заходит в область геометрической тени, т. е. волна огибает края отверстия.

Принцип Гюйгенса решает лишь задачу о направлении распространения волнового фронта, но не затрагивает вопроса об амплитуде, а следовательно, и об интенсивности волн, распространяющихся по разным направлениям. Френель вложил в принцип Гюйгенса физический смысл, дополнив его идеей интерференции вторичных волн.

Таким образом, волны, распространяющиеся от источника, являются результатом интерференции всех когерентных вторичных волн.

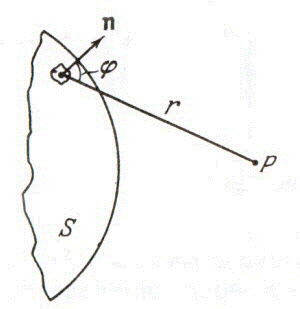
Согласно принципу Гюйгенса - Френеля каждый элемент волновой поверхности S служит источником вторичной сферической волны, амплитуда которой пропорциональна величине dS. От каждого участка волновой поверхности в точку P приходит колебание:

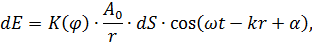
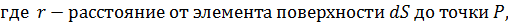
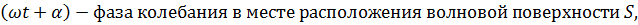
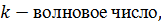
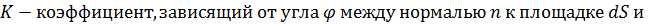
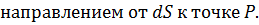
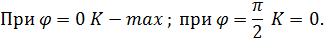
Результирующее колебание в точке P – суперпозиция колебаний, взятых для всей волновой поверхности S:

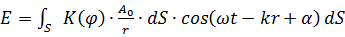
Метод зон Френеля.

Френель показал, что нахождение амплитуды результирующего колебания может быть осуществлено алгебраическим суммированием.

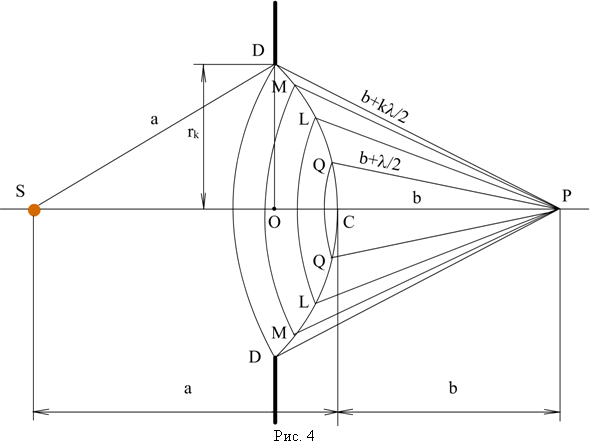
Определим амплитуду светового колебания, возбуждаемого в точке P сферической волной, распространяющейся в однородной среде от точечного источника S. Волновые поверхности симметричны относительно прямой SP. Френель разбил волновую поверхность на кольцевые зоны такого размера, чтобы расстояния от краёв зоны до P отличались на 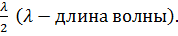Подобное разбиение фронта волны на зоны можно выполнить, проведя с центром в точке P сферы радиусами 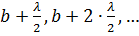. Такие зоны носят название зон Френеля.

Расстояние 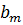от внешнего края 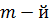зоны до точки P равно:

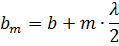
При не слишком больших m площади зон Френеля примерно одинаковы:

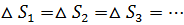
Расстояние 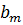медленно растёт с номером зоны m. Угол φ также растёт с m. Всё это приводит к тому, что амплитуда 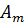монотонно убывает:

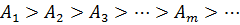
Так как колебания от соседних зон проходят до точки P расстояния, отличающиеся на , то в точку P они приходят в противоположной фазе и при наложении эти колебания

будут взаимно ослаблять друг друга. Поэтому амплитуда результирующего светового колебания в точке P будет равна:

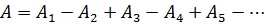
Запишем это выражение в виде:

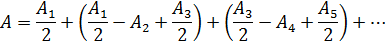
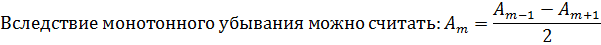
Тогда выражения в скобках будут равны нулю, и формула упрощается:

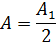
Таким образом, амплитуда результирующих колебаний в произвольной точке P равна половине амплитуды центральной зоны Френеля.