Тепловые двигатели и холодильные

Машины. Цикл Карно и его к. п. д . для

Идеального газа

Из формулировки второго начала термодинамики по Кельвину следует, что вечный двигатель второго рода — периодически действующий двигатель, совершающий работу за счет охлаждения одного источника теплоты, — невозможен. Для иллюстрации этого положения рассмотрим работу теплового двигателя (исторически второе начало термодинамики и возникло из анализа работы тепловых двигателей).

Принцип действия теплового двигателя приведен на рис. 85. От термостата* с более высокой температурой T₁ называемого нагревателем, за цикл отнимается количество теплоты Q₁, a термостату с более низкой температурой Т₂,называемому холодильником, за цикл передается количество теплоты Q₂, при этом совершается работа A = Q₁ — Q₂.

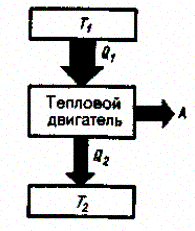
Рис. 85

Чтобы термический коэффициент полезного действия теплового двигателя (56.2) был равен 1, необходимо выполнение условия Q₂ = 0, т. е. тепловой двигатель должен иметь один источник теплоты, а это невозможно. Так, французский физик и инженер Н. Л. С. Карно (1796 — 1832) показал, что для работы теплового двигателя необходимо не менее двух источников теплоты с различными температурами, иначе это противоречило бы второму началу термодинамики.

Двигатель второго рода, будь он возможен, был бы практически вечным. Охлаждение, например, воды океанов на 1° дало бы огромную энергию. Масса воды в Мировом океане составляет примерно 10¹⁸ т, при охлаждении которой на 1° выделилось бы примерно 10²⁴ Дж теплоты, что эквивалентно полному сжиганию 10¹⁴ т угля. Железнодорожный состав, нагруженный этим количеством угля, растянулся бы на расстояние 10¹⁰ км, что приблизительно совпадает с размерами Солнечной системы!

Процесс, обратный происходящему в тепловом двигателе, используется в холодильной машине, принцип действия которой представлен на рис. 86. Системой за цикл от термостата с более низкой температурой Т₂отнимается количество теплоты Q₂и от дается термостату с более высокой температурой Т₁количество теплоты Q₁. Для кругового процесса, согласно (56.1), Q = A,но, по условию, Q = Q₂ - Q₁ < 0,поэтому A < 0 и Q₂ – Q₁ = - A, или Q₁ = Q₂ + A, т. е. количество теплоты Q₁,отданное системой источнику теплоты при более высокой температуре Т₁, больше количества теплоты Q₂, полученного от источника теплоты при более низкой температуре Т₂на величину работы, совершенной над системой. Следовательно, без совершения работы нельзя отбирать теплоту от менее нагретого тела и отдавать ее более нагретому. Это утверждение есть не что иное, как второе начало термодинамики в формулировке Клаузиуса.

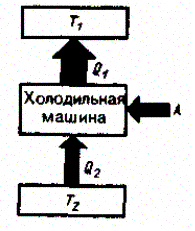
Рис. 86

Однако второе начало термодинамики не следует представлять так, что оно совсем запрещает переход теплоты от менее нагретого тела к более нагретому. Ведь именно такой переход осуществляется в холодильной машине. Но при этом надо помнить, что внешние силы совершают работу над системой, т. е. этот переход не является единственным результатом процесса.

Основываясь на втором начале термодинамики, Карно вывел теорему, носящую теперь его имя: из всех периодически действующих тепловых машин, имеющих одинаковые температуры нагревателей (Т₁) и холодильников (Т₂),наибольшим к. п. д. обладают обратимые машины; при этом к. п. д. обратимых машин, работающих при одинаковых температурах нагревателей (Т₁) и холодильников (Т₂), равны друг другу и не зависят от природы рабочего тела (тела, совершающего круговой процесс и обменивающегося энергией с другими телами), а определяются только температурами нагревателя и холодильника.

Карно теоретически проанализировал обратимый наиболее экономичный цикл, состоящий из двух изотерм и двух адиабат. Его называют циклом Карно. Рассмотрим прямой цикл Карно, в котором в качестве рабочего тела используется идеальный газ, заключенный в сосуд с подвижным поршнем.

Цикл Карно изображен на рис. 87, где изотермические расширение и сжатие заданы соответственно кривыми 1—2 и 5—4, а адиабатические расширение и сжатие — кривыми 2—3и 4—7. При изотермическом процессе U= const, поэтому, согласно (54.4), количество теплоты Q₁, полученное газом от нагревателя, равно работе расширения А₁₂, совершаемой газом при переходе из состояния 1 в состояние 2:

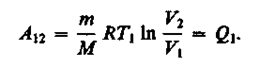(59.1)

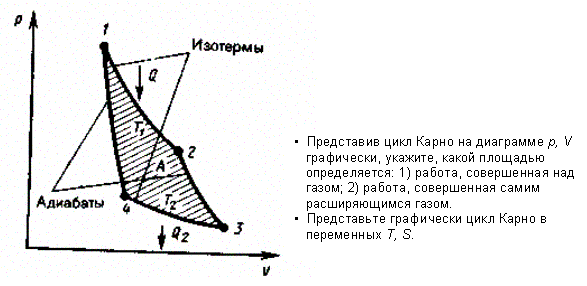
Рис. 87

При адиабатическом расширении 2—3теплообмен с окружающей средой отсутствует и работа расширения А₂₃совершается за счет изменения внутренней энергии (см. (55.1) и (55.8)):

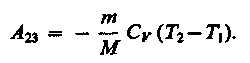
Количество теплоты Q₂, отданное газом холодильнику при изотермическом сжатии, равно работе сжатия A₃₄:

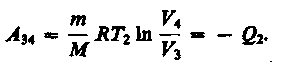(5.92)

Работа адиабатического сжатия

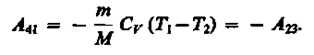
Работа, совершаемая в результате кругового процесса,

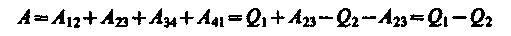
и, как можно показать, определяется площадью, заштрихованной на рис. 87. Термический к. п. д. цикла Карно, согласно (56.2),

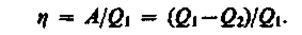
Применив уравнение (55.5) для адиабат 2—3 и 4—1, получим

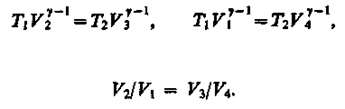(5.93)

Подставляя (59.1) и (59.2) в формулу (56.2) и учитывая (59.3), получаем

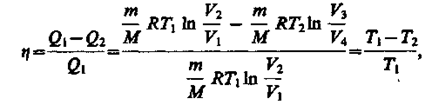(59.4)

т. е. для цикла Карно к. п. д. действительно определяется только температурами нагревателя и холодильника. Для его повышения необходимо увеличивать разность температур нагревателя и холодильника. Например, при T₁ = 400 К и T₂ = 300 К h = 0,25. Если же температуру нагревателя повысить на 100 К, а температуру холодильника понизить на 50 К, то h = 0,5. К. п. д. всякого реального теплового двигателя из-за трения и неизбежных тепловых потерь гораздо меньше вычисленного для цикла Карно.

Обратный цикл Карно положен в основу действия тепловых насосов. В отличие от холодильных машин тепловые насосы должны как можно больше тепловой энергии отдавать горячему телу, например системе отопления. Часть этой энергии отбирается от окружающей среды с более низкой температурой, а часть — получается за счет механической работы, производимой, например, компрессором.

Теорема Карно послужила основанием для установления термодинамической шкалы температур. Сравнив левую и правую части формулы (59.4), получим (59.5)

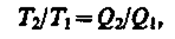
т. е. для сравнения температур T₁и T₂двух тел необходимо осуществить обратимый цикл Карно, в котором одно тело используется в качестве нагревателя, другое — холодильника. Из равенства (59.5) видно, что отношение температур тел равно отношению отданного в этом цикле количества теплоты к полученному. Согласно теореме Карно, химический состав рабочего тела не влияет на результаты сравнения температур, поэтому такая термодинамическая шкала не связана со свойствами какого-то определенного термометрического тела. Отметим, что практически таким образом сравнивать температуры трудно, так как реальные термодинамические процессы, как уже указывалось, являются необратимыми.

Задачи

9.1. Азот массой 1 кг находится при температуре 280 К. Определить: 1) внутреннюю энергию молекул азота; 2) среднюю кинетическую энергию вращательного движения молекул азота, Газ считать идеальным. [1) 208 кДж; 2) 83,1 кДж]

9.2. Определить удельные теплоемкости c_vи c_pнекоторого двухатомного газа, если плотность этого газа при нормальных условиях 1,43 кг/м³. [с_v =650 Дж/(кг×К). c_p =910 Дж/(кг×К)]

9.3. Водород массой т = 20 г был нагрет на DT=100 К при постоянном давлении. Определить: 1) количество теплоты Q, переданное газу; 2) приращение DU внутренней энергии газа; 3) работу А расширения. [1) 29,3 кДж; 2) 20,9 кДж; 3) 8,4 кДж]

9.4 Кислород объемом 2 л находится под давлением 1 МПа. Определить, какое количество теплоты необходимо сообщить газу, чтобы увеличить его давление вдвое в результате изохорного промесса. [5 кДж]

9.5. Некоторый газ массой 2 кг находится при температуре 300 К и под давлением 0,5 МПа. В результате изотермического сжатия давление газа увеличилось в три раза. Работа, затраченная на сжатие, A = -1,37 кДж. Определить: 1) какой это газ; 2) первоначальный удельный объем газа. [1) гелий; 2) 1,25 м³/кг]

9.6. Двухатомный идеальный газ занимает объем V₁ = 1 л и находится под давлением p₁=0,1 МПа. После адиабатического сжатия газ характеризуется объемом V₂и давлением p₂.

В результате последующего изохорного процесса газ охлаждается до первоначальной температуры, а его давление р₃ = 0,2МПа. Определить: 1) объем V₂; 2) давление p₂.Представить эти процессы графически. [1) 0,5 л; 2) 0,26 МПа]

9.7. Идеальный газ количеством вещества v=2 моль сначала изобарно нагрели так, что его объем увеличился в n=2 раза, а затем изохорно охладили так, что давление газа уменьшилось вnп=2 раза. Определить приращение энтропии в ходе указанных процессов. [11,5 Дж/К]

9.8. Тепловая машина, совершая обратимый цикл Карно, за один цикл совершает работу 1 кДж. Температура нагревателя 400 К, а холодильника 300 К. Определить: 1) к. п. д. машины; 2) количество теплоты, получаемое машиной от нагревателя за цикл; 3) количество теплоты, отдаваемое холодильнику за цикл. [1) 25%; 2) 4 кДж; 3) 3 кДж]

9.9. Идеальный газ совершает цикл Карно, термический к. п. д. которого равен 0,3. Определить работу изотермического сжатия газа, если работа изотермического расширения составляет 300 Дж. [-210 Дж]

Глава 10

Реальные газы, жидкости

И твердые тела