Акустооптические модуляторы

Принцип действия акустооптического модулятора основан на зависимости показателя преломления оптической среды от внешнего давления (эффект фотоупругости). Под действием ультразвуковых волн (f»10⁴¸10¹³ Гц) благодаря фотоупругости происходит модуляция показателя преломления среды, вследствие чего среда приобретает свойства оптической фазовой решетки, период которой равен длине акустической волны. Примером таких материалов являются кристаллы ТеО₂ (диоксид теллура), LiNbO₃ (ниобат лития), PbMoO₄ (молибдат свинца) и т.д. В этих кристаллах давление создается акустическими волнами, генерируемыми пьезоэлектрическим преобразователем.

Рис.5.7. Ход лучей в акустооптическом модуляторе.

Ход лучей в акустооптическом модуляторе имеет вид, показанный на рис. 5.7.

Акустические волны созданные генератором (пьезоэлектрический кристалл) образуют ряд горизонтальных линий с одинаковыми показателями преломления, так называемую решетку Брэгга. Она перемещается со скоростью U_ак и обеспечивает отражение входного луча. Акустическая волна, распространяющаяся в оптически прозрачной среде, вызывает периодическое изменение его показателя преломления n:

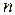
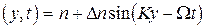
такую среду можно рассматривать как фазовую дифракционную решетку с периодом, равным длине ультразвуковой волны 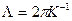, где K=W/U_ак -волновое число, W-циклическая частота, U_ак - скорость акустической волны .

Характер дифракции света на акустических волнах существенно зависит от параметра .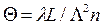

В случае 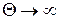наблюдается дифракция Брэгга. Дифракционная картина Брэгга состоит из двух максимумов: нулевого и первого порядков дифракции. Отражение происходит при определенных углах, так называемых углах Брэгга.

Если шаг решетки 2s равен оптической длине волны света в материале, тогда: 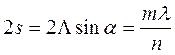(5.12)

и происходит интерференция всех отраженных волн. Здесь L=U_ак/ 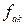-длина акустической волны; 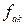- частота генератора акустических волн, 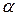-угол Брэгга в кристалле, m-дифракционный порядок; 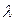-длина оптической волны, n-показатель преломления материала.

С точки зрения применений наибольший интерес представляет угол Брэгга за пределами кристалла 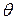. По закону Снеллиуса: 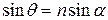или из (5.12): 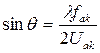. (5.13)

Как видно из формулы (5.13) при U_ак =const. угол Брэгга 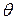зависит только от частоты генератора акустических волн 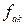и оптической длины волны .

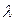При модуляции мощности генератора акустических волн происходит модуляция интенсивности отклоненного светового луча. Интенсивность отклоненного светового луча в первом максимуме выражается как:

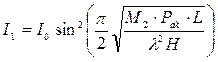
(5.14)

где 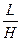- геометрические размеры акустического волнового пучка; 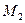-акустическое качество материала; P_ак – акустическая мощность. Как видно из формулы (5.14), увеличивая P_ак можно в принципедобиться 100% - ной эффективности модулятора. Акустическое качество зависит от следующих физических характеристик материала: 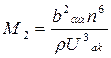, (5.15)

где 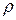- плотность среды; 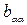-компонента тензора наведенной анизотропии.

Соотношение (5.14) является модуляционной характеристической акустооптического модулятора света.

Акустооптический модулятор характеризуется следующими параметрами: 1) Нелинейная функция преобразования, которая позволяет определить рабочую точку для обеспечения необходимого значения контрастности и глубины модуляции лазерного излучения:

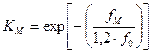, (5.16)

где f_M – частота модуляции; f₀=0,35/t; t=0,85V_ak/L – длительность фронта нарастания акустической волны.

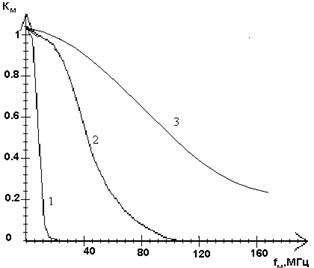Рис. 5.8. Примеры нелинейной функцией преобразования. 1- f₀ = 80 MГц; 2 – f₀ = 200 MГц; 3 – f₀ = 800 МГц.

2) Контрастность модуляции лазерного излучения, определяемая отношением его максимальной интенсивности, прошедшего через модулятор к минимальному значению: 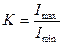, (5.17)

3) Глубина модуляции оптического излучения, которая определяется как: 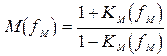. (5.18)

Еще одной особенностью акустооптического модулятора является то, что в результате акустооптического взаимодействия лазерного излучения с движущейся дифракционной решеткой, частота лазерного излучения смещается на величину акустической частоты 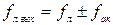.