Задачи для контрольных работ 4 страница

3.64Два конденсатора емкостями С₁ = 2 мкФ и С₂ = 5 мкФ заряжены до напряжений U₁ = 100 В и U₂ = 150 В соответственно. Определить напряжение на обкладках конденсаторов после их соединения обкладками, имеющими разноименные заряды.

3.65Два одинаковых плоских воздушных конденсатора емкостью С = 100 пФ каждый соединены в батарею последовательно. Определить, на сколько изменится емкость С батареи, если пространство между пластинами одного из конденсаторов заполнить парафином.

3.66Два конденсатора емкостями С₁ = 5 мкФ и С₂ = 8 мкФ соединены последовательно и присоединены к батарее с ЭДС = 80 В. Определить заряды Q₁ и Q₂ конденсаторов и разности потенциалов U₁ и U₂ между их обкладками.

3.67Плоский конденсатор состоит из двух круглых пластин радиусом R = 10 см каждая. Расстояние между пластинами d = 2 мм. Конденсатор присоединен к источнику напряжения U = 80 В. Определить заряд Q и напряженность Е поля конденсатора в двух случаях: а) диэлектрик – воздух; б) диэлектрик – стекло.

3.68Два металлических шарика радиусом R₁ = 5 см и R₂ = 10 см имеют заряды Q₁ = 40 нКл и Q₂ = -2 нКл соответственно. Найти энергию W, которая выделится при разряде, если шары соединить проводником.

3.69Пространство между пластинами плоского конденсатора заполнено двумя слоями диэлектрика: стекла толщиной d₁ = 0,2 см и слоем парафина толщиной d₂ = 0,2 см. Разность потенциалов между обкладками U = 300 В. Определить напряженность Е поля и падение потенциалов в каждом из слоев.

3.70Плоский конденсатор с площадью пластин S = 200 см²каждая заряжен до разности потенциалов U = 2 кВ. Расстояние между пластинами d = 2 см. Диэлектрик – стекло. Определить энергию W поля конденсатора и плотность энергии w поля.

3.71Два проводящих шара с радиусами R₁ = 8 см и R₂ = 20 см, находящихся на большом расстоянии друг от друга, имели заряды q₁ = 40 нКл и q₂ = –20 нКл. Каковы будут заряды на шарах после соединения их проводником? Емкостью проводника, соединяющего шары пренебречь.

3.72Два проводящих шара с радиусами R₁ = 10 см и R₂ = 30 см находятся друг от друга на расстоянии, которое во много раз больше радиуса второго шара. На первый шар помещен заряд q₁ = 10 нКл. Каковы будут заряды на шарах после соединения их проводником, если второй шар не был заряжен? Емкостью проводника, соединяющего шары пренебречь.

3.73Конденсатор емкости C₁ = 4 мкФ, заряженный до напряжения U₁ = 10 В, соединен параллельно с заряженным до напряжения U₂ = 20 В конденсатором емкости C₂ = 6 мкФ (соединили разноименно заряженные обкладки конденсаторов). Какой заряд окажется на пластинах первого конденсатора после соединении?

3.74Найти количество теплоты, выделившееся при соединении одноименно заряженных конденсаторов C₁ = 2 мкФ и C₂ = 0,5 мкФ. Разности потенциалов между обкладками конденсаторов U₁ = 100 В и U₁ = 50 В.

3.75Найти количество теплоты, выделившееся при соединении незаземленных обкладок конденсаторов с емкостями C₁ = 2 мкФ и C₂ = 0,5 мкФ. Разности потенциалов до соединения между незаземленными обкладками конденсаторов и землей U₁ = 100 В и U₂ = –5 0 В.

3.76Катушка и амперметр соединены последовательно и подключены к источнику тока. К клеммам катушки присоединен вольтметр с сопротивлением r = 4 кОм. Амперметр показывает силу тока I = 0,3 А, вольтметр – напряжение U = 120 В. Определить сопротивление R катушки. Определить относительную погрешность , которая будет допущена при измерении сопротивления, если пренебречь силой тока, текущего через вольтметр.

3.77От батареи, ЭДС которой e = 600 В, требуется передать энергию на расстояние l = 1 км. Потребляемая мощность Р = 5 кВт. Найти минимальные потери мощности в сети, если диаметр медных проводящих проводов d = 0,5 см.

3.78При внешнем сопротивлении R₁ = 8 Ом сила тока в цепи I₁ = 0,8 А, при сопротивлении R₂ = 15 Ом силы тока I₂ = 0,5 А. Определить силу тока I_к.з. короткого замыкания источника ЭДС.

3.79ЭДС батареи e = 24 В. Наибольшая сила тока, которую может дать батарея, I_max = 10 A. Определить максимальную мощность P_max, которая может выделяться во внешней цепи.

3.80Аккумулятор с ЭДС e = 12 В заряжается от сети постоянного тока с напряжением U = 15 В. Определить напряжение на клеммах аккумулятора, если его внутреннее сопротивление R_i = 10 Ом.

3.81От источника с напряжением U = 800 В необходимо передать потребителю мощность Р = 10 кВт на некоторое расстояние. Какое наибольшее сопротивление может иметь линия передачи, чтобы потери энергии в ней не превышали 10% от передаваемой мощности?

3.82При включении электромотора в сеть с напряжением U = 220 В он потребляет ток I = 5 А. Определить мощность, потребляемую мотором, и его КПД, если сопротивление R обмотки мотора равно 6 Ом.

3.83За время t = 20 c при равномерно возрастающей силе тока от нуля до некоторого максимума в проводнике сопротивлением R = 5 Ом выделилось количество теплоты Q = 4 кДж. Определить скорость нарастания силы тока. Если сопротивление проводника R = 5 Ом.

3.84Сила тока впроводнике (R = 100 Ом) изменяется со временем по закону I = I₀e , где I₀ = 20 А, a = 10² с^–1. Определить количество теплоты, выделившееся в проводнике за время t = 10^–2 с.

3.85Сила тока в проводнике сопротивлением R = 10 Ом за время t = 50 с равномерно нарастает от I₁ = 5 А до I₂ = 10 А. Определить количество теплоты Q, выделившейся за это время в проводнике.

3.86Сила тока впроводнике изменяется со временем по закону I = I₀sin . Найти заряд Q, проходящий через поперечное сечение проводника за время t, равное половине периода Т, если начальная сила тока I₀ = 10 А, циклическая частота с^-1.

3.87За время t = 10 с при равномерно возрастающей силе тока от нуля до некоторого максимума в проводнике выделилось количество теплоты Q = 40 кДж. Определить среднюю силу тока <I> в проводнике, если его сопротивление R = 25 Ом.

3.88За время t = 8 с при равномерно возраставшей силе тока в проводнике сопротивлением R = 8 Ом выделилось количество теплоты Q = 500 Дж. Определить заряд q, проходящий в проводнике, если сила тока в начальный момент времени равна нулю.

3.89Определить количество теплоты Q, выделившееся за время t = 10 c в проводнике сопротивлением R = 10 Ом, если сила тока в нем, равномерно уменьшаясь, изменилась от I₁ = 10 А до I₂ = 0.

3.90Сила тока в цепи изменяется по закону I = I₀ e . Определить количество теплоты, которое выделится в проводнике сопротивлением r = 20 Ом за время, в течение которого ток уменьшится в е раз. Коэффициент a принять равным 2×10^–2 с^-1.

4.1Бесконечно длинный провод с током А изогнут так, как это показано на рис. 6. Определить магнитную индукцию 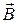в точке . Радиус дуги см.

4.2Магнитный момент тонкого проводящего кольца А·м². Определить магнитную индукцию 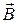в точке , находящейся на оси кольца и удаленной от точек кольца на расстояние см (рис. 7).

Рисунок 6 Рисунок 7

4.3По двум скрещенным под прямым углом бесконечно длинным проводам текут токи и ( А). Определить магнитную индукцию 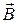в точке А (рис. 8). Расстояние см.

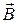4.4По бесконечно длинному проводу, изогнутому так, как это показано на рис. 9, течет ток А. Определить магнитную индукцию в точке О. Радиус дуги см.

Рисунок 8 Рисунок 9

4.5По тонкому кольцу радиусом см течет ток А. Определить магнитную индукцию 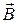на оси кольца в точке А (рис. 10). Угол .

4.6По двум бесконечно длинным проводам, скрещенным под прямым углом, текут токи и ( А). Определить магнитную индукцию 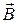в точке А, равноудаленной от проводов на расстояние см (рис. 11).

Рисунок 10 Рисунок 11

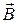4.7По бесконечно длинному проводу, изогнутому так, как это показано на рис. 12, течет ток А. Определить магнитную индукцию в точке О. Радиус дуги см.

4.8По тонкому кольцу течет ток А. Определить магнитную индукцию 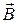в точке А, равноудаленной от точек кольца на расстояние см (рис. 13). Угол .

Рисунок 12 Рисунок 13

4.9По двум бесконечно длинным, прямым параллельным проводам текут одинаковые токи А. Определить магнитную индукцию 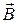в точке А (рис. 14), равноудаленной от проводов на расстояние см. Угол .

4.10Бесконечно длинный провод с током А изогнут так, как это показано на рис. 15. Определить магнитную индукцию 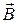в точке А, лежащей на биссектрисе прямого угла на расстоянии см от его вершины.

4.11По двум длинным параллельным проводам текут в одинаковом направлении токи I₁ = 10 A и I₂ = 12 A. Расстояние между проводами a = 10 см. Определить напряженность 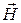магнитного поля в точке, удаленной от первого проводника на r₁ = 8 см и от второго на r₂ = 6 см.

Рисунок 14 Рисунок 15

4.12Решить предыдущую задачу при условии, что токи текут в противоположном направлениях, а точка удалена от первого провода на r₁ = 15 см и от второго на r₂ = 10 см.

4.13По тонкому проводнику, изогнутому в виде правильного шестиугольника со стороной a = 10 см, идет ток I =20 A. Определить магнитную индукцию 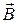в центре шестиугольника.

4.14Два круговых витка радиусом R = 4 см каждый расположены в параллельных плоскостях на расстоянии d = 10 см друг от друга. По виткам в одном направлении текут токи I₁ = I₂ = 2 A. Найти напряженность 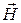магнитного поля на оси витков в точке, находящейся на равном расстоянии от них.

4.15Два круговых витка радиусом R = 2 см каждый расположены в двух взаимно перпендикулярных плоскостях так, что центры этих витков совпадают. По виткам текут токи I₁ = I₂ = 5 A. Найти напряженность 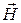магнитного поля в центре этих витков.

4.16По трем параллельным прямым проводам, находящимся на одинаковом расстоянии см друг от друга, текут одинаковые токи А. В двух проводах направления токов совпадают. Вычислить для каждого из проводов отношение силы, действующей на него, к его длине.

4.17Квадратная проволочная рамка расположена в одной плоскости с длинным прямым проводом так, что две ее стороны параллельны проводу. По рамке и проводу текут одинаковые токи А. Определить силу F, действующую на рамку, если ближайшая к проводу сторона рамки находится от него на расстоянии, равном ее длине.

4.18Тонкий провод длиной см изогнут в виде полукольца и помещен в магнитное поле ( мТл) так, что площадь полукольца перпендикулярна линиям магнитной индукции. По проводу пропустили ток А. Определить силу 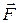, действующую на провод. Подводящие провода направлены вдоль линий магнитной индукции.

4.19Квадратный контур со стороной см, по которому течет ток А, свободно установился в однородном магнитном поле (B =10 мТл). Определить изменение потенциальной энергии контура при повороте вокруг оси, лежащей в плоскости контура, на угол .

4.20Тонкое проводящее кольцо с током А помещено в однородное магнитное поле ( мТл). Плоскость кольца перпендикулярна линиям магнитной индукции. Радиус R кольца равен 20 см. Найти силу F, растягивающую кольцо.

4.21Квадратная рамка из тонкого провода может свободно вращаться вокруг горизонтальной оси, совпадающей с одной из сторон. Масса рамки равна 20 г. Рамку поместили в однородное магнитное поле ( Тл), направленное вертикально вверх. Определить угол , на который отклонилась рамка от вертикали когда по ней пропустили ток А.

4.22По круговому витку радиусом см течет ток А. Виток расположен в однородном магнитном поле ( мТл) так, что нормаль к плоскости контура составляет угол с вектором 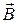. Определить изменение потенциальной энергии контура при его повороте на угол в направлении увеличения угла .

4.23По тонкому кольцу радиусом см равномерно распределен заряд с линейной плотностью нКл/м. Кольцо вращается относительно оси, перпендикулярной плоскости кольца и проходящей через его центр, с частотой с^-1. Определить магнитный момент , обусловленный вращением кольца.

4.24Диск радиусом см несет равномерно распределенный по поверхности заряд ( нКл/м²). Определить магнитный момент , обусловленный вращением диска, относительно оси, проходящей через его центр и перпендикулярной плоскости диска. Угловая скорость вращения диска рад/с.

4.25Стержень длиной см заряжен равномерно распределенным зарядом с линейной плотностью мкКл/м. Стержень вращается с частотой с^-1 относительно оси, перпендикулярной стержню и проходящей через его конец. Определить магнитный момент , обусловленный вращением стержня.

4.26Протон движется по окружности радиусом см с линейной скоростью v = 10⁶ м/с. Определить магнитный момент , создаваемый эквивалентным круговым током.

4.27Тонкое кольцо радиусом см несет равномерно распределенный заряд нКл. Кольцо вращается с угловой скоростью рад/с относительно оси, совпадающей с одним из диаметров кольца. Найти магнитный момент , обусловленный вращением кольца.

4.28Заряд мкКл равномерно распределен по стержню длиной см. Стержень вращается с угловой скоростью рад/с относительно оси, перпендикулярной стержню и проходящей через его середину. Найти магнитный момент , обусловленный вращением стержня.

4.29Сплошной цилиндр радиусом см и высотой см несет равномерно распределенный по объему заряд ( мкКл/м³). Цилиндр вращается с частотой с^-1 относительно оси, совпадающей с его геометрической осью. Найти магнитный момент цилиндра, обусловленный его вращением.

4.30По тонкому стержню длиной см равномерно распределен заряд нКл. Стержень вращается с частотой с^-1 относительно оси, перпендикулярной стержню и проходящей через стержень на расстоянии от одного из его концов. Определить магнитный момент , обусловленный вращением, стержня.

4.31Два иона разных масс с одинаковыми зарядами влетели в однородное магнитное поле, стали двигаться по окружностям радиусами см и см. Определить отношение масс ионов, если они прошли одинаковую ускоряющую разность потенциалов.

4.32Однозарядный ион натрия прошел ускоряющую разность потенциалов кВ и влетел перпендикулярно линиям магнитной индукции в однородное поле ( Тл). Определить относительную атомную массу А иона, если он описал окружность радиусом см.

4.33Электрон прошел ускоряющую разность потенциалов В и, влетев в однородное магнитное поле мТл, стал двигаться по винтовой линии с шагом мм. Определить радиус R винтовой линии.

4.34Альфа-частица прошла ускоряющую разность потенциалов В и, попав в однородное магнитное поле, стала двигаться по винтовой линии радиусом см и шагом см. Определить магнитную индукцию В поля.