Физические основы эксперимента

Содержание

Лабораторная работа №11. Изучение статистических закономер-

ностей.…………………………………………………………………….3

Лабораторная работа № 12. Определение коэффициента вязкости

воздуха..……………………………..…………………………………….15

Лабораторная работа № 14. Определение показателя адиабаты γ

методом Клемана и Дезорма…………………………………………..

Лабораторная работа № 15. Проверка закона возрастания энтро-

пии……………………………………………………………………….

Лабораторная работа №11

Изучение статистических закономерностей

Цель работы: изучение характера распределения дроби в установке Гальтона и распределения термоэлектронов по модулям скоростей.

Описание лабораторной установки и оборудования

В лабораторной работе выполняются два эксперимента.

Эксперимент 1. Исследование распределения дроби в горизонтальной плоскости при прохождении её через систему решёток.

Эксперимент проводится на установке, (так называемая доска Гальтона), схема которой приведена на рис. 1

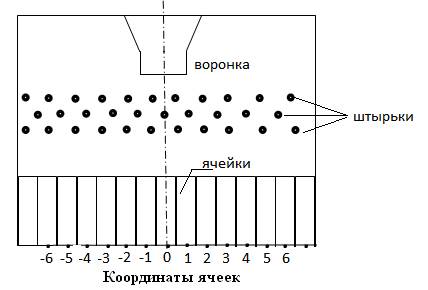
Рис. 1 Схема экспериментальной установки

Она представляет собой плоский вертикальный ящик с прозрачной передней стенкой.

Через воронку в установку насыпают дробь, которая падая вниз через систему штырьков, попадает в ячейки. При соударении со штырьками происходит отклонение дробинок в горизонтальной плоскости, носящее случайный характер. С одной стороны установки имеется 3 ряда штырьков, с другой – 12. На прозрачные стенки ячеек нанесены деления, по которым можно определить уровень заполнения ячеек дробью.

Эксперимент 2. Исследование распределения термоэлектронов по модулю их скорости.

Эксперимент проводится на установке, электрическая схема которой, приведена на рис. 2.

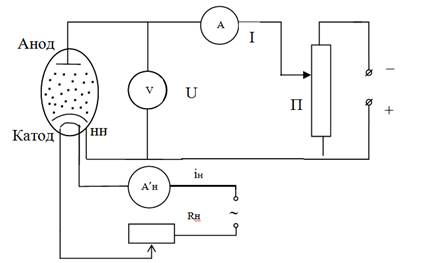
Рис.2. Схема экспериментальной установки

Основной частью установки является электронная лампа, в которой катод - нить, натянутая по оси лампы, окружён цилиндрическим анодом. НН – нить накала подключается к источнику переменного напряжения. C помощью реостата Rн можно изменять величину тока накала i_н. При этом будет изменяться число термоэлектронов, испускаемых катодом в единицу времени.

Между анодом и катодом создаётся тормозящее поле, величину которого можно изменять с помощью потенциометра П. Изменяя задерживающее напряжение U, которое измеряется вольтметром V, можно снять зависимость анодного тока I, измеряемого амперметром А, от задерживающего напряжения. Из этой зависимости можно найти функцию распределения термоэлектронов по скоростям.

Общие сведения

Физические основы эксперимента

Все макроскопические тела состоят из огромного числа атомов и молекул, которые находятся в непрерывном хаотическом движении. В силу этого скорости и координаты отдельных молекул – величины случайные. Поэтому в совокупном поведении отдельных молекул появляются статистические закономерности. Их изучение и делает возможным описание макросистем на основе сведений о свойствах отдельных частиц системы.

Статистическая физика связывает параметры макроскопических тел (давление, плотность, теплопроводность, вязкость и т. п.) со средними значениями микропараметров молекул (скоростью, координатами и импульсом). Математическим аппаратом статистической физики является теория вероятности.

Вероятность появления некоторого значения 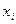дискретной случайной величины 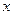есть величина 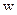_i, равная

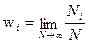, (1)

где 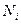- число наблюдений, в которых было получено данное значение 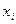, 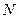- общее число наблюдений.

Вероятностью того, что непрерывная случайная величина 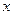(например, скорость молекулы) будет иметь значение в интервале от 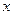до 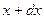, называется величина 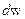, равная

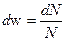, (2)

где 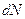- количество наблюдений, в которых величина 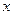имела значение в интервале от 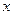до 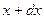, 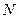- общее число наблюдений.

Вероятность 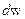будет зависеть от значения случайной величины 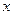и от ширины интервала 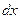, т.е.

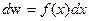. (3)

Функция 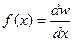(4)

называется функцией распределения вероятностей или плотностью вероятности. Она показывает, какова вероятность того, что случайная величина будет иметь значение в единичном интервале вблизи некоторого значения .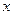

Средние значения случайной влечены Х определяются по формулам: для дискретной случайной величины

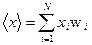, (5)

для непрерывной случайной величины

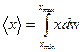. (6)

С учётом (3): 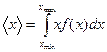(7)

На рис.3 приведён один из возможных примеров функции распределения. В соответствии с формулой (3) площадь заштрихованной полоски равна .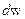

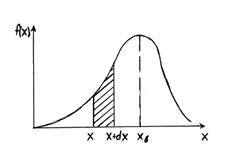
Рис.3

Вероятность того, что величина 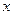может принять хотя бы какое-нибудь значение из всех возможных (достоверное событие) очевидно равна единице, т.е.

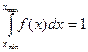, (8)

где интегрирование ведётся по всем возможным значениям 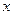. Из этого следует, что вся площадь под кривой 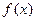на рис. 3 равна единице. Формула (8) называется условием нормировки функции распределения.

Значение случайной величины 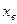, при котором плотность вероятности принимает максимальное значение, называется наиболее вероятным.

Отыскание математического вида функции распределения – одна из основных задач статистической физики.

Приведём примеры некоторых функций распределения.

а) Нормальное распределение или распределение Гаусса

Математический вид функций распределения:

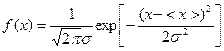, (9)

где s -- стандартное (среднеквадратичное отклонение), которое характеризует рассеяние (разброс) случайной величины х вокруг её среднего значения <х> или «ширину» графика нормального распределения. График функции распределения приведены на рис.4

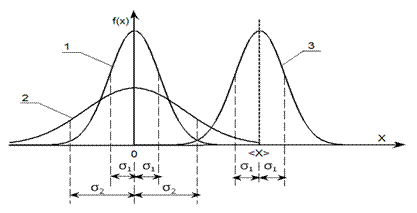
Рис. 4

Характеристики распределения	График 1	График 2	График 3
Среднеквадратическое отклонение, σ	σ1	σ2 >σ1	σ1
Среднее значение, х			<x>

Распределению Гаусса подчиняются случайные ошибки экспериментальных измерений. Нормальным (гауссовским) является распределение молекул идеального газа по проекциям скоростей Vx на произвольную ось [1, 2, 3]:

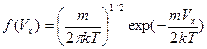, (10)

где m – средняя масса молекул, k- постоянная Больцмана, Т- температура.

В данной работе в первом эксперименте исследуется распределение дроби в горизонтальном направлении после прохождения её через систему рассеивающих штырьков (см. рис. 1), которое при определённых условиях является распределением Гаусса. Поясним, почему это происходит.

Выйдя из воронки, любая дробинка движется первоначально вертикально вниз. При ударе о штырьки дробинка случайным образом отклоняется от вертикали, приобретая какую-то скорость Vx в горизонтальном направлении, и попадает в некоторую ячейку. Чем больше Vx, тем в более удалённую от центра ячейку попадёт дробинка.

Просыпав всю дробь через систему штырьков, можно получить гистограмму заполнения ячеек дробью (см.рис.5).

Вероятность того, что наугад взятая дробинка попадёт в ячейку с координатой х, будет определяться по формуле:

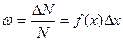, (11)

где 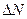- число дробинок, попавших в данную ячейку, 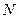- общее число дробинок, 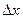- ширина ячейки, 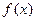- функция распределения дробинок по ячейкам.

О виде функции распределения 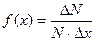можно будет судить по величине 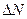, т.к. 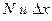-величины фиксированные.

В свою очередь 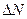пропорционально высоте заполнения ячейки, т.к. их ширина одинакова. Поэтому линия, огибающая верхний уровень дроби в ячейках, даст график функции 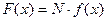, описывающей распределение дроби по ячейкам (см. рис.5).

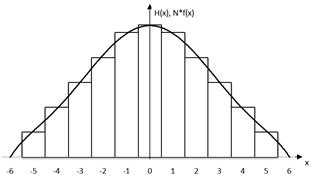
Рис. 5 Распределение дроби по ячейкам

В данном опыте отклонение дроби равновероятно в обе стороны от центра воронки. Это является характерной чертой распределения Гаусса. Однако при экспериментальном исследовании этого распределения возможно действие каких-либо факторов, которые нарушат симметрию. Поэтому для проверки симметричности получаемого в эксперименте распределения используют величину, которая называется коэффициентом асимметрии. Он рассчитывается по формуле [4, 5]:

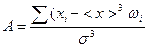. (12)

При А = 0 гистограмма является симметричным графиком.

При А > 0 гистограмма сдвинута в сторону больших значений х,

при А < 0 – в сторону меньших х.

Среднее значение <x> находится по формуле:

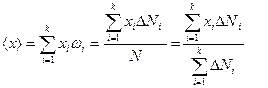. (13)

Т. к. ∆Ni пропорционально высоте заполнения ячеек дробью Нi, то вместо (13) получим:

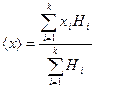. (14)

Среднеквадратичное отклонение распределения в данном случае можно рассчитать по формуле[1]: σ²= 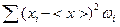, где

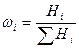, (15)

Наиболее вероятное значение х_в определяется по максимуму графика функции распределения. Установка позволяет изменять количество штырьков и получить две функции распределения.

б) Распределение Максвелла

Математический вид функции распределения в общем случае:

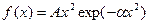, (16)

где А и α – некоторые константы.

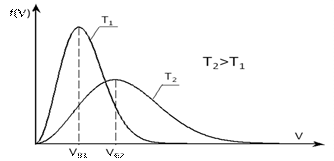
Рис. 6

Такой вид имеет распределение молекул идеального газа по модулю скорости.

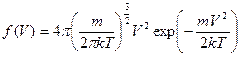. (17)

Графики функции (17) для двух разных температур газа приведены на рис.6. Здесь V_В1 и V_В2 –наиболее вероятные скорости молекул при температурах Т₁ и Т₂. Исследуя (17) на максимум, получим, что

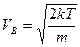. (18)

В данной лабораторной работе во 2-ом эксперименте находится функция распределения термоэлектронов по модулю их скорости. Эксперимент базируется на следующих положениях.

Если между катодом и анодом приложить напряжение U₁ (см. рис.2), то до анода дойдут только те электроны, у которых кинетическая энергия 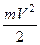не меньше работы 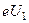(е – заряд электрона) по преодолению тормозящего поля, т.е.

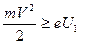(19)

или 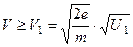и начальная скорость будет направлена строго от катода к аноду.

Если приложить другое напряжение U₂ = U₁ + DU, то до анода дойдут электроны, у которых скорость

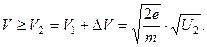
Поэтому при изменении напряжения от U₁ до U₂ анодный ток
уменьшится на величину 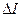, определяемую количеством электронов DN, ²отсекаемых² от анода ежесекундно.

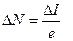. (20)

С другой стороны ∆N - это количество электронов, скорости которых лежат в интервале от 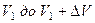, и оно равно: 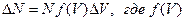- функция распределения термоэлектронов по модулю скорости, N – число всех электронов, испускаемых катодом ежесекундно строго в направлении анода. Оно остаётся величиной постоянной при постоянной температуре катода. Поэтому график зависимости 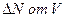будет описывать распределение термоэлектронов по модулю скорости при фиксированном значении .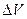