Прием сигналов с неопред. фазой(некогеренчтый прием)

Многие каналы можно описать моделью с флуктуирующей фазой. Нередко фаза флуктуирует довольно быстро, и точную её оценку получить не удаётся. Кроме того, оценка фазы требует иногда применения сложных устройств. Поэтому даже в тех случаях, когда принципиально можно оценить начальную фазу приходящего сигнала, порой от этого отказываются и используют алгоритм, построенный в предположении, что начальная фаза приходящего сигнала не известна и может принимать любое значение на интервале (0, 2π). Такой метод приёма называется некогерентным. Алгоритм оптимального некогерентного приёма впервые получен Л.М. Финком.Для вывода правила оптимального некогерентного приёма будем исходить из логарифма отношения правдоподобия lnΛ_i для сигнала s_i(t), которое при точно известной начальной фазе выражается формулой (5.23). Используя представление для сигнала (4.44), где γ — известный коэффициент передачи канала, а θ - случайный сдвиг в канале, формулу для lnΛ_i можно (после устремления в (5.23) Δt→0) записать так:

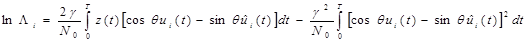. (5.67)

Здесь lnΛ_i является случайной величиной, принимающей различные значения при различных θ. Правило максимума правдоподобия в такой ситуации заключается в выборе такого решения, для которого математическое ожидание Λ_i будет наибольшим. При нахождении 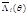заметим, что второй интеграл в правой части (5.67) от θ не зависит и равен энергии E_Пi сигнала u_i(t) на входе канала (на передатчике).

Основной понятийный аппарат теории информации. Частное количество информации. Энтропия источника сообщении. Условная энтропия.Количество информации передаваемое по каналу связи.Пропускная способность.

Частное количество информации i(a):

1.Количество информации i(a)должно быть аддитивной функцией, т.е. для пары взаимно независимых сообщений a₁,a₂ оно должно равняться сумме количества информации в каждом из них, т.е. i(a₁,a₂) ⁼ i(a₁) + i(a₂)

2. Количество информации, содержащейся в достоверном сообщении (имеющем вероятность Р(а) = 1), равно нулю.

3. Количество информации должно зависеть только от вероятности переданно­го сообщения, т.е.i(a) =f{P(a)).

4. Количество информации должно быть непрерывной функцией от Р(а).

Можно показать, что единственная функция, удовлетворяющая всем этим условиям, имеет вид i(a)= -logP(a)≥0.

Энтропия источника сообщений. Для того, чтобы получить исчерпывающую информационную характеристику источника сообщений, который, вообще говоря, может выдавать последовательности не­ограниченной длины, нужно вычислить предел среднего количества информа­ции i(aⁿ), отнесённый к одному символу последовательности. Полученная ве­личина, Н(А), называется энтропией источника сообщений, т.е. Н( А) =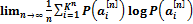

Определим условную энтропию Н(X|Y):
Н(X|Y)=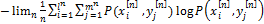

Условная энтропия обладает следующими свойствами:

1. H(X|Y)≥0

2.Если вход и выход канала связаны взаимно однозначно, т.е.

P(x| y)=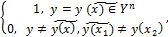

то H(X|Y)=0

3.H(X|Y) ≤(X)

4.H(X|Y) =H(X), тогда, и только тогда, когда P ( x | y ) =Р(х)