Расчет рекуперативного теплообменника
Теплообменным аппаратом (теплообменником) называют устройство, предназначенное для передачи теплоты от одной жидкости (горячего теплоносителя) к другой жидкости (холодному теплоносителю). В работе выполняется расчет рекуперативного теплообменника, в котором горячий и холодный теплоносители разделены стенкой.
1. Задание
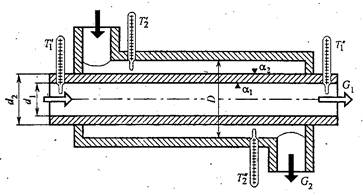 1.1. Определить площадь теплопередающей поверхности рекуперативного теплообменника типа "труба в трубе" (рисунок). Расчеты необходимо выполнить для прямоточного и противоточного движения теплоносителей. Потерями теплоты от теплообменника в окружающую среду пренебречь.
1.1. Определить площадь теплопередающей поверхности рекуперативного теплообменника типа "труба в трубе" (рисунок). Расчеты необходимо выполнить для прямоточного и противоточного движения теплоносителей. Потерями теплоты от теплообменника в окружающую среду пренебречь.
| Расчетная схема теплообменника |
1.2. Исходные данные
Горячий теплоноситель движется по внутренней трубе, его температура на входе равна  , а расход составляет
, а расход составляет 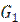 кг/с. Холодный теплоноситель движется по кольцевому каналу между трубами и нагревается от температуры
кг/с. Холодный теплоноситель движется по кольцевому каналу между трубами и нагревается от температуры 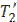 до
до 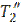 ; его расход составляет
; его расход составляет 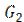 кг/с. Исходные данные для расчета выбираются из табл. 5 и 6 приложения (по указанию преподавателя). Выбранные исходные данные записываются в табл. 3.1.
кг/с. Исходные данные для расчета выбираются из табл. 5 и 6 приложения (по указанию преподавателя). Выбранные исходные данные записываются в табл. 3.1.
Таблица 3.1.
Данные для расчета теплообменника
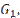 кг/с кг/с | 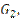 кг/с кг/с | 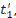 0C 0C | 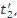 0C 0C | 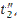 0C 0C | 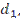 мм мм | 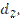 мм мм |  мм мм | Материал трубок | Теплоноситель |
2. Методические указания к выполнению расчетов
Для определения площади поверхности нагрева теплообменного
аппарата необходимо вычислить его линейный коэффициент теплопередачи  , Bт/(м∙
, Bт/(м∙ 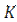 ):
):
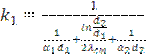 , (3.1)
, (3.1)
где 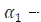 коэффициент теплоотдачи от горячей жидкости к стенке трубы, Вт/(
коэффициент теплоотдачи от горячей жидкости к стенке трубы, Вт/( 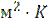 );
); 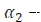 коэффициент теплоотдачи от наружной поверхности внутренней трубы к холодной жидкости, Вт/(
коэффициент теплоотдачи от наружной поверхности внутренней трубы к холодной жидкости, Вт/( 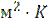 );
); 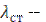 коэффициент теплопроводности материала стенки внутренней трубы, Вт/(
коэффициент теплопроводности материала стенки внутренней трубы, Вт/( 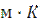 );
);
Коэффициенты теплоотдачи 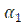 и
и 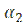 определяют, решая соответствующие критериальный уравнения. Определяемым является критерий Нуссельта:
определяют, решая соответствующие критериальный уравнения. Определяемым является критерий Нуссельта:  ,
,
где 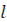 - характерный линейный размер, м;
- характерный линейный размер, м; 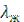 - коэффициент теплопроводности жидкости, Вт/(м∙
- коэффициент теплопроводности жидкости, Вт/(м∙ 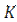 ).
).
В зависимости от решаемой задачи (течение жидкости в трубах, движение жидкости вдоль пластины, поперек или в продольном направлении труб и др.), характера движения жидкости и ряда других факторов критерий Нуссельта может быть выражен как функция критериев Прандтля (Рг), Грасгофа (Gr) или Рейнольдса (Re).
Общее критериальное уравнение для конвективного теплообмена:
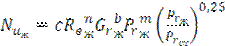 .
.
Характер движения жидкости в трубах может быть ламинарным и турбулентным. О режиме течения судят по величине критерия Рейнольдса  , где W - средняя скорость движения жидкости, м/с; d -внутренний диаметр трубы, м;
, где W - средняя скорость движения жидкости, м/с; d -внутренний диаметр трубы, м; 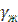 - коэффициент кинематической вязкости жидкости, м2/с. Если
- коэффициент кинематической вязкости жидкости, м2/с. Если 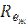 < 2320, то движение жидкости будет ламинарным. При
< 2320, то движение жидкости будет ламинарным. При 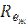 = 2,32 •103... 104 режим движения является переходным. При
= 2,32 •103... 104 режим движения является переходным. При 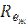 > 104 в трубе устанавливается развитое турбулентное движение жидкости.
> 104 в трубе устанавливается развитое турбулентное движение жидкости.
При ламинарном движении жидкости встречаются два режима изотермного движения: вязкостный и вязкостно-гравитационный. Вязкостный режим соответствует движению жидкости при отсутствии естественной конвекции. Вязкостно-гравитационный режим имеет место тогда, когда вынужденное движение жидкости сопровождается естественной конвекцией. Для того чтобы установить, оказывает ли влияние на теплоотдачу естественная конвекция, требуется вычислить произведение критериев Грасгофа и Прандтля ( 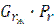 ).
).
Критерий Грасгофа 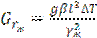 , где
, где 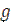 - ускорение свободного падения, м/с2;
- ускорение свободного падения, м/с2; 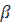 - коэффициент объемного теплового расширения жидкости, (
- коэффициент объемного теплового расширения жидкости, ( 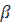 =
=  ,
,  ;
; 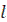 - характерный линейный размер, для горизонтальной трубы равный ее диаметру, м; ΔT - температурный напор, равный
- характерный линейный размер, для горизонтальной трубы равный ее диаметру, м; ΔT - температурный напор, равный 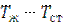 ,
,  .
.
Физические параметры жидкостей, а также величину критерия 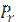 выбирают из табл. 7 приложения в зависимости от средней температуры теплоносителей:
выбирают из табл. 7 приложения в зависимости от средней температуры теплоносителей:
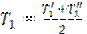 и
и  .
.
Температура стенки трубы равна 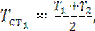
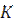 .
.
Если ( 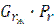 ) >
) > 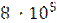 , то естественная конвекция не оказывает существенного влияния на теплоотдачу и режим движения жидкости вязкостный, в противном случае вязкостно - гравитационный.
, то естественная конвекция не оказывает существенного влияния на теплоотдачу и режим движения жидкости вязкостный, в противном случае вязкостно - гравитационный.
При вязкостном режиме рекомендуется определять средний коэффициент теплоотдачи в прямых гладких трубах по формуле:
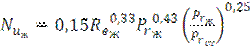 (3.2).
(3.2).
Для вязкостно-гравитационного режима расчеты среднего коэффициента теплоотдачи в прямых гладких трубах производить по выражению: 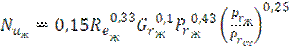 (3.3)
(3.3)
Для определения среднего коэффициента теплоотдачи при развитом турбулентном движении рекомендуется следующее уравнение:
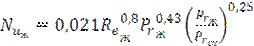 (3.4).
(3.4).
Плотность теплового потока на 1 м трубы:
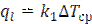 (3.5),
(3.5),
где 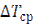 - среднелогарифмический температурный напор,
- среднелогарифмический температурный напор, 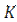 . Для теплообменных аппаратов с прямотоком:
. Для теплообменных аппаратов с прямотоком:
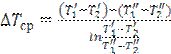 , (3.6)
, (3.6)
а для аппаратов с противотоком:
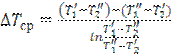 . (3.7)
. (3.7)
2.1. Порядок выполнения расчетов
1. Температуру горячего теплоносителя на выходе из теплообменника определить из уравнения теплового баланса при условии, что потери в окружающую среду отсутствуют. Так как количество теплоты, передаваемой горячим теплоносителем, 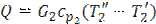 , Bт, то
, Bт, то 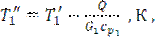 где
где 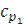 и
и  - соответственно массовые изобарные теплоемкости горячего и холодного теплоносителей. Их значения принять постоянными и равными: для воды - 4190, для масла -2081 Дж/(кг∙К).
- соответственно массовые изобарные теплоемкости горячего и холодного теплоносителей. Их значения принять постоянными и равными: для воды - 4190, для масла -2081 Дж/(кг∙К).
2. Скорость движения горячего теплоносителя 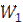 и холодного
и холодного 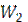 вычислить из выражений
вычислить из выражений  и
и 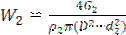 .
.
где  и
и 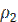 - плотности теплоносителей в зависимости от температуры, кг/м3 (табл. 7 приложения).
- плотности теплоносителей в зависимости от температуры, кг/м3 (табл. 7 приложения).
3. Вычислить значения критерия Рейнольдса  для обеих сред, определив затем характер движения теплоносителя. В случае ламинарного движения определить режим течения (вязкостный или вязкостно- гравитационный). При вычислении критерия
для обеих сред, определив затем характер движения теплоносителя. В случае ламинарного движения определить режим течения (вязкостный или вязкостно- гравитационный). При вычислении критерия 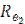 принять эквивалентный диаметр
принять эквивалентный диаметр  .
.
4. В соответствии с характером движения жидкости выбрать одно из критериальных уравнений (3.2), (3.3) или (3.4) с целью определения величины критериев Нуссельта 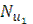 и
и 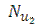 , характеризующих интенсивность теплообмена на поверхностях внутренней трубы со стороны горячего и холодного теплоносителей. Температуру
, характеризующих интенсивность теплообмена на поверхностях внутренней трубы со стороны горячего и холодного теплоносителей. Температуру 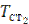 принять равной температуре
принять равной температуре 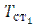 .
.
5. По найденным значениям критериев Нуссельта вычислить величины коэффициентов теплоотдачи 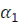 и
и  .
.
6. Коэффициент теплопередачи 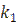 определить по выражению (3.1). Коэффициент теплопроводности материала стенки трубы выбрать по табл. 8 приложения в зависимости от
определить по выражению (3.1). Коэффициент теплопроводности материала стенки трубы выбрать по табл. 8 приложения в зависимости от 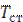 .
.
7. Вычислить средние логарифмические температурные напоры для случаев прямотока и противотока по формулам (3.6) и (3.7).
8. Плотность теплового потока определить по формуле (3.5),
9. Длина трубы теплообменника находится как 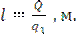
10. Поверхность нагрева определяется как 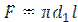 , м2.
, м2.
11. Выполнить анализ результатов расчета для прямоточного и противоточного движений теплоносителей: определить разницу величины поверхностей теплоотдачи для обоих случаев, выразив ее в процентах. Сделать выводы.
ПРИЛОЖЕНИЕ
Таблица 1
Исходные данные к контрольной работе № 1
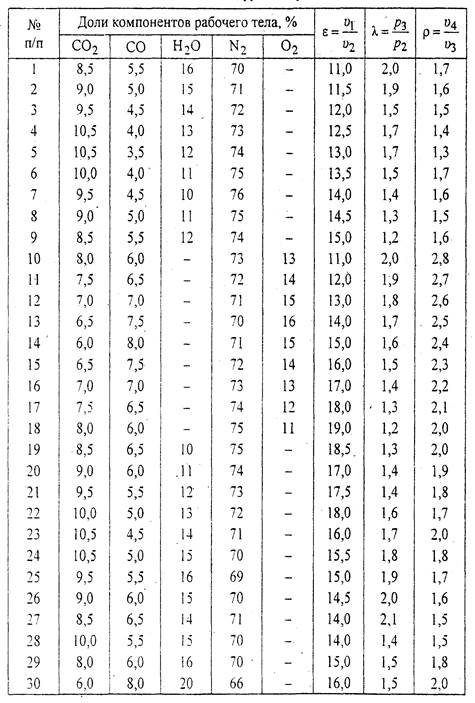
Таблица 2
Характеристики газов
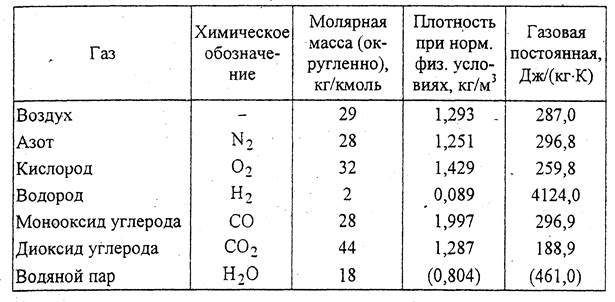 Примечание: параметры водяного пара условно приведены к нормальному состоянию.
Примечание: параметры водяного пара условно приведены к нормальному состоянию.
Таблица 3
Исходные данные к контрольной работе №2

Таблица 4
Свойства сухого пара
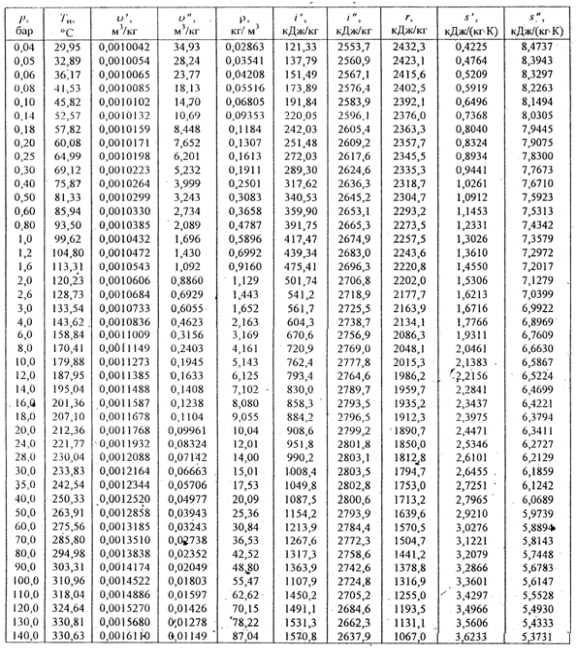
Таблица 5
Исходные данные для расчета теплообменника.
Горячий и холодный теплоносители – вода
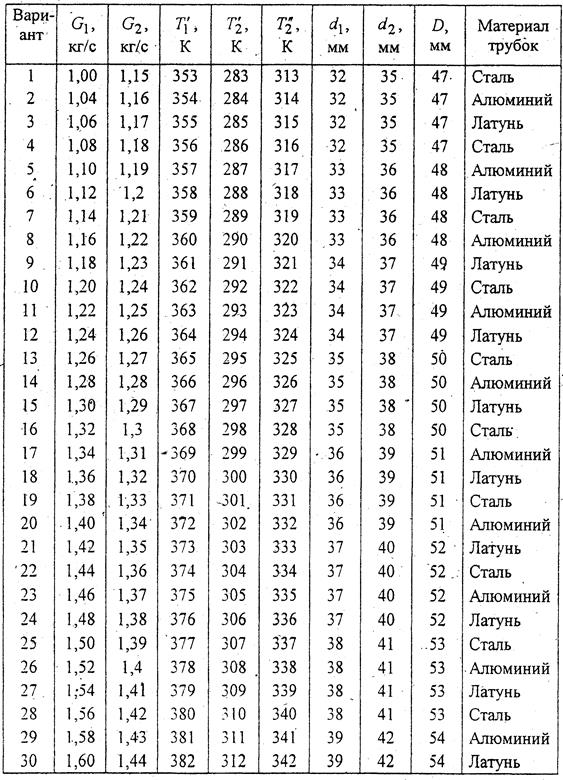
Таблица 6
Исходные данные для расчета теплообменника.
Горячий теплоноситель – масло, холодный – вода
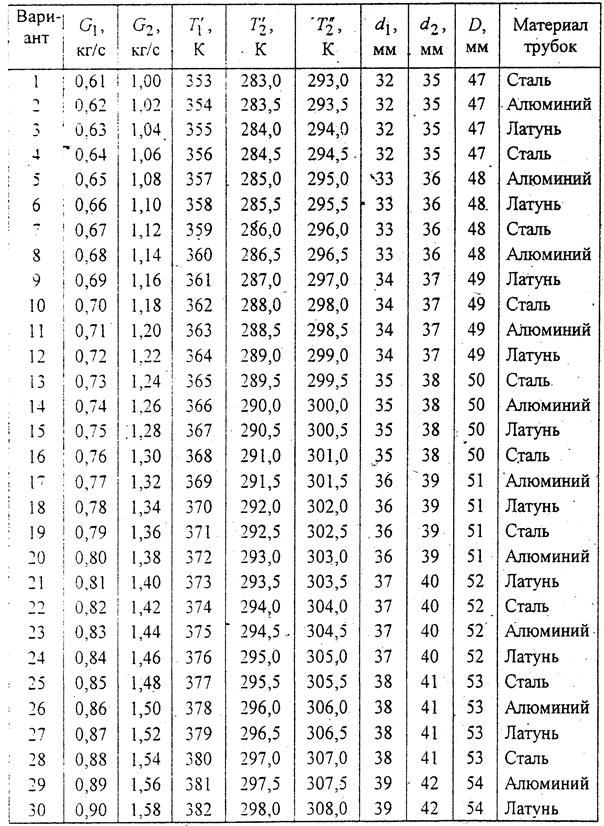
Таблица 7
Физические свойства жидкостей
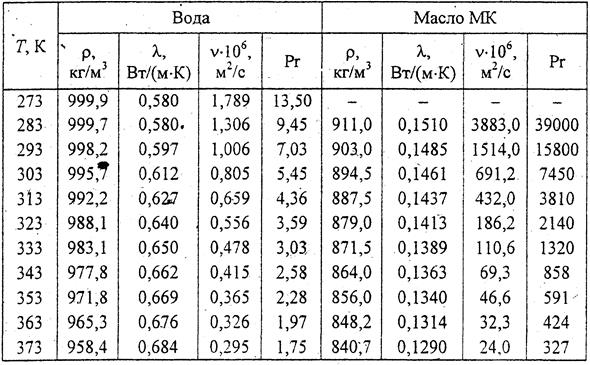
Таблица 8
Значение коэффициента теплопроводности металлов

Список использованных источников
1.Теплотехника:Учеб. для вузов/ В.Н. Луканин, М.Г. Шатров, Г.М. Камфер и др.; Под ред. Луканина. – 3-е изд.,испр. – М.: Высш. шк.,2002. – 671 с.: ил.
2. Архаров А.М. Теплотехника: Учеб. для студентов вузов / Под общ. ред. В.И. Крутова -М.: Машиностроение, 1986.-432 с.
3. Нащокин В.В. Техническая термодинамика и теплопередача: Учеб. пособие для вузов. - М.: Высш. шк., 1980. - 496 с.
4. Афанасьев В.Н, Задачник по технической термодинамике и теории тепломассообмена: Учеб. пособие для энергомашиностроит. спец. вузов / Под ред. В.И, Крутова и Г.Б. Петражицкого. - М.: Высш шк 1986 -383с.
5. Тихомиров К.В. Теплотехника, теплогазоснабжение и вентиляция. - М.: Стройиздат, 1984. - 274 с.
6. Исаев С.И. Теория тепломассообмена: Учеб. для энергомашино-строит. спец. вузов / С.И. Исаев, И.А. Кожинов, В.И.' Кофанов и др.; Под ред. А.И. Леонтьева. - М.: Высш. шк., 1979. -495 с.
