Энтропия, ее статистическое толкование и связь с термодинамической вероятностью

Понятие энтропии введено в 1865г. Р. Клаузиусом. Для выяснения физическо­го содержания этого понятия рассматри­вают отношение теплоты Q, полученной телом в изотермическом процессе, к темпе­ратуре Т теплоотдающего тела, называе­мое приведенным количеством теплоты.

Приведенное количество теплоты, со­общаемое телу на бесконечно малом участке процесса, равно dQ/T. Строгий теоретический анализ показывает, что приведенное количество теплоты, сообща­емое телу в любом обратимом круговом процессе, равно нулю:

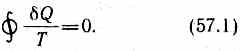
Из равенства нулю интеграла (57.1), взя­того по замкнутому контуру, следует, что подынтегральное выражение dQ/T есть полный дифференциал некоторой фун­кции, которая определяется только состоя­нием системы и не зависит от пути, каким система пришла в это состояние. Таким образом,

Функция состояния, дифференциалом ко­торой является dQ/T, называется энтро­пиейи обозначается S.

Из формулы (57.1) следует, что для обратимых процессов изменение энтропии

DS=0. (57.3)

В термодинамике доказывается, что эн­тропия системы, совершающей необрати­мый цикл, возрастает:

DS>0. (57.4)

Выражения (57.3) и (57.4) относятся только к замкнутым системам, если же система обменивается теплотой с внешней средой, то ее энтропия может вести себя любым образом. Соотношения (57.3) и (57.4) можно представить в виде не­равенства Клаузиуса

DS³0, (57.5)

т. е. энтропия замкнутой системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов).

Если система совершает равновесный переход из состояния 1 в состояние 2, то, согласно (57.2), изменение энтропии

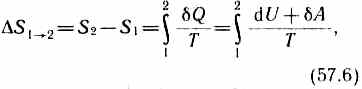
где подынтегральное выражение и преде­лы интегрирования надо выразить через величины, характеризующие исследуемый процесс. Формула (57.6) определяет эн­тропию лишь с точностью до аддитивной постоянной. Физический смысл имеет не сама энтропия, а разность энтропии.

Исходя из выражения (57.6), найдем изменение энтропии в процессах иде­ального газа. Так как dU=(m/M)C_v dT,

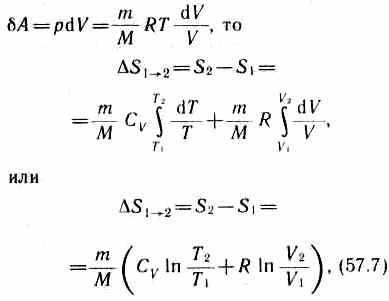
т. е. изменение энтропии DS_1®2 идеального газа при переходе его из состояния 1 в со­стояние 2 не зависит от вида процесса перехода 1®2.

Так как для адиабатического процесса dQ = 0, то DS=0 и, следовательно, S=const, т. е. адиабатический обратимый

процесс протекает при постоянной энтро­пии. Поэтому его часто называют изоэнтропийным процессом.Из формулы (57.7) следует, что при изотермическом процессе (T₁=T₂)

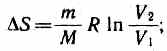
при изохорном процессе (V₁=V₂)

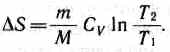
Энтропия обладает свойством аддитивности: энтропия системы равна сумме энтропии тел, входящих в систему. Свойством аддитивности обладают также внутренняя энергия, масса, объем (темпе­ратура и давление таким свойством не обладают).

Более глубокий смысл энтропии вскры­вается в статистической физике, энтропия связывается с термодинамической веро­ятностью состояния системы. Термодина­мическая вероятностьW состояния систе­мы — это число способов, которыми может быть реализовано данное состояние мак­роскопической системы, или 'число микро­состояний, осуществляющих данное мак­росостояние (по определению, W³1, т. е. термодинамическая вероятность не есть вероятность в математическом смыс­ле (последняя £1!)).

Согласно Больцману (1872), энтропия S системы и термодинамическая вероят­ность связаны между собой следующим образом:

S = klnW, (57.8)

где k — постоянная Больцмана. Таким об­разом, энтропия определяется логариф­мом числа микросостояний, с помощью которых может быть реализовано данное макросостояние. Следовательно, энтропия может рассматриваться как мера вероятности состояния термодинамиче­ской системы. Формула Больцмана (57.8) позволяет дать энтропии следующее ста­тистическое толкование: энтропия являет­ся мерой неупорядоченности системы. В самом деле, чем больше число микросо­стояний, реализующих данное макрососто­яние, тем больше энтропия. В состоянии

равновесия — наиболее вероятного состо­яния системы — число микросостояний максимально, при этом максимальна и эн­тропия.

Так как реальные процессы необрати­мы, то можно утверждать, что все про­цессы в замкнутой системе ведут к увели­чению ее энтропии — принцип возраста­ния энтропии.При статистическом толко­вании энтропии это означает, что про­цессы в замкнутой системе идут в на­правлении увеличения числа микросостоя­ний, иными словами, от менее вероятных состояний к более вероятным, до тех пор пока вероятность состояния не станет мак­симальной.

Сопоставляя выражения (57.5) и (57.8), видим, что энтропия и термоди­намическая вероятность состояний за­мкнутой системы могут либо возрастать (в случае необратимых процессов), либо оставаться постоянными (в случае обрати­мых процессов).

Отметим, однако, что эти утверждения имеют место для систем, состоящих из очень большого числа частиц, но могут нарушаться в системах с малым числом частиц. Для «малых» систем могут на­блюдаться флуктуации, т. е. энтропия и термодинамическая вероятность состоя­ний замкнутой системы на определенном отрезке времени могут убывать, а не воз­растать, или оставаться постоянными.